What is a Number Line? Definition, Examples and Applications
Table of Contents
Introduction
What are Number Lines?
Number lines are visual representations of numbers, typically displayed as a straight line with numbers marked at regular intervals. They are used to illustrate the concept of magnitude and order of numbers, making it easier to understand their relative positions and relationships. It helps us to compare between numbers and perform basic mathematical operations.
Analogy of Definition
Definition
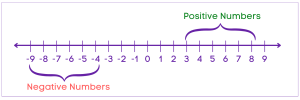
A number line is a mathematical tool that represents numbers as points on a line. It helps in visualizing the order of numbers, understanding positive and negative values, and performing operations such as addition, subtraction, multiplication, and division. In a number line, 0 lies in the center whereas positive numbers are on the right side of 0 and negative numbers are on the left. The number line can be extended infinitely in both the directions.
Method
Using Number Lines
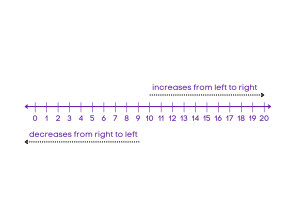
Number lines can be used to perform various mathematical operations, including addition, subtraction, multiplication, and division. They are also helpful in understanding concepts such as fractions, decimals, and integers, as well as solving equations and inequalities. In a number line, the numbers increase while moving from left to right while the number decrease when you move from right to left.
Learn more about Number Lines with fun activties at ChimpVine.
Examples
Using a Number Line to Add and Subtract
Example 1: Addition
To add 3 and 5 using a number line, start at 3 and move 5 units to the right. The point where you land represents the sum, which is 8.
Example 2: SubtractionÂ
To subtract 7 from 10 using a number line, start at 10 and move 7 units to the left. The point where you land represents the difference, which is 3.
Quiz
Tips and Tricks
1. Addition on a Number Line
Tip:Â To add numbers using a number line, start at the first number and move to the right by the value of the second number to find the sum. First we begin at 3, then we move 5 steps towards the right which gives us 8.
Calculation: 3 + 5 = 8
2. Subtraction on a Number Line
Tip:Â To subtract numbers using a number line, start at the first number and move to the left by the value of the second number to find the difference. First we begin at 10, then we move seven steps to the left which gives us 3.Â
Calculation: 10 – 7 = 3
3. Multiplication on a Number Line
Tip:Â To multiply numbers using a number line, repeated addition can be used to find the product. First we begin at 3, then we skip 4 numbers 3 times towards the right which gives us 12.Â
Calculation: 3 x 4 = 12
4. Division on a Number Line
Tip:Â To divide numbers using a number line, repeated subtraction can be used to find the quotient.
Calculation: 12 ÷ 3 = 4
5. Fractions on a Number Line
Tip:Â To represent fractions on a number line, divide the interval between two consecutive integers into equal parts and locate the fraction accordingly.
Calculation: 1/2 is located between 0 and 1 on the number line.
6. Comparision on a Number Line
Tip:Â To compare using a number line is simple. The number of the left is smaller than the number on the right.
Calcution: If we are to compare -1 and 0, on a number line, -1 lies on the left of 0 which makes 0 greater than -1.
Real life application
Story: “The Number Line Adventure of Sam and Emma”
Sam and Emma, two curious students, embarked on an adventure to explore the real-life applications of number lines and their significance in solving everyday problems.
Challenge 1: The Grocery Shopping Quest
Sam and Emma went grocery shopping and encountered a dilemma when trying to compare the prices of different items. Using a number line, they were able to visually represent the prices and determine which item offered the best value for money. They could compare which price was high and which was low.Â
Challenge 2: The Time Management Challenge
As part of a time management challenge, Sam and Emma needed to schedule their daily activities effectively. They used a number line to create a timeline and allocate time slots for each task, ensuring optimal productivity throughout the day.
Challenge 3: The Budgeting Adventure
In a budgeting exercise, Sam and Emma had to allocate their monthly income to various expenses. By using a number line, they were able to visualize their income and expenses, making it easier to manage their budget effectively.
FAQ's
Number lines help in understanding the order of numbers, performing operations, visualizing fractions and decimals, and solving equations. They provide a visual representation of mathematical concepts such as addition, subtraction, multiplication, division and comparision, making it easier to comprehend and apply them.
Number lines can be used to introduce the concept of positive and negative numbers by representing them as points on the line. Children can learn to compare, order, and perform operations with positive and negative values using the number line as a visual aid.
Yes, there are printable number lines available online, which can be used for educational purposes, classroom activities, and homework assignments. These resources provide visual support for learning and practicing mathematical concepts.
Yes, number lines are effective tools for teaching fractions and decimals. They help in visualizing the relative positions of fractions and decimals, comparing their magnitudes, and performing operations with them.
Number lines have practical applications in various fields, such as time management, budgeting, scheduling, and decision-making. They provide a visual framework for organizing and analyzing information, making them valuable tools in problem-solving and planning.
By understanding the concept of number lines and their applications, individuals can enhance their mathematical skills and problem-solving abilities, both in academic and real-life settings. Whether it’s solving equations, visualizing fractions, or managing time and resources, number lines play a crucial role in making complex concepts more accessible and manageable.
Like? Share it with your friends
Facebook
Twitter
LinkedIn