Adding Mixed Fractions – Steps with Examples
Table of Contents
Introduction
Mixed Fractions
In the realm of mathematics, mixed fractions play a crucial role in representing quantities that fall between whole numbers and fractions. Adding mixed fractions is a fundamental skill that is essential for various mathematical operations. Let’s explore the methods and techniques for adding mixed fractions with like denominators and unlike denominators.
Analogy of Definition
What are Mixed Fractions?
A mixed fraction consists of a whole number and a proper fraction. It is represented in the form of a\tfrac{b}{c} where “a” is the whole number, “b” is the numerator, and “c” is the denominator. Adding mixed fractions involves combining the whole numbers and fractions to obtain the sum of the quantities.
Method
Adding Mixed Fractions with Like Denominators
When the fractions have the same denominators, the process of adding mixed fractions becomes simpler. You can directly add the whole numbers and the fractions, ensuring that the denominators remain the same.
Let’s say we want to add the following mixed fractions:
3\tfrac{1}{4} + 2\tfrac{2}{4}
Step 1: Convert mixed fractions to improper fractions: Rewrite each mixed fraction as an improper fraction.
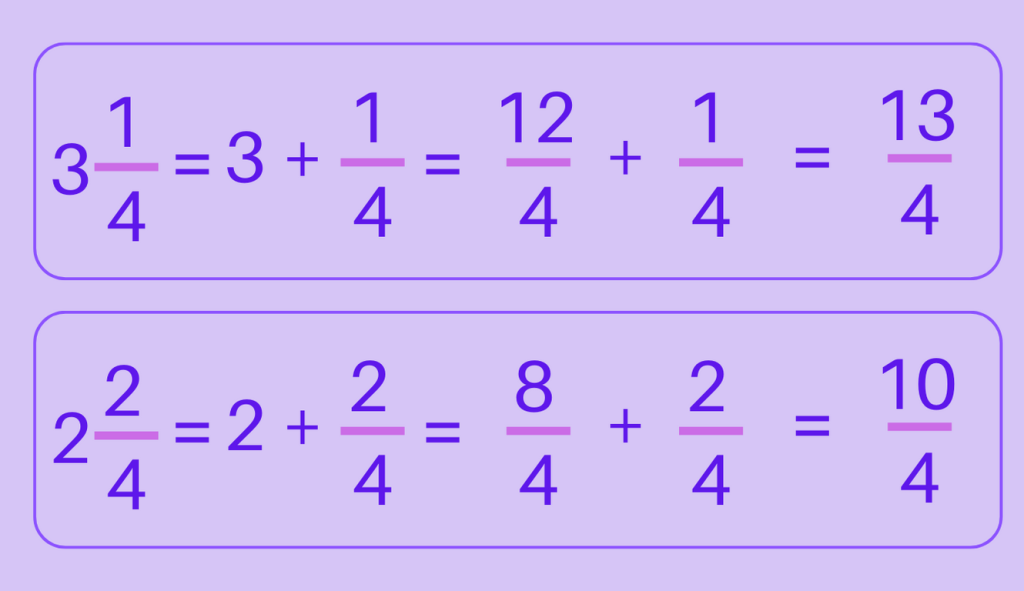
Step 2: Add the numerators of the improper fractions while keeping the denominator the same.
Step 3: Convert the improper fraction back to a mixed fraction (if necessary). If the result is an improper fraction, convert it back to a mixed fraction.
Hence, the final answer will be
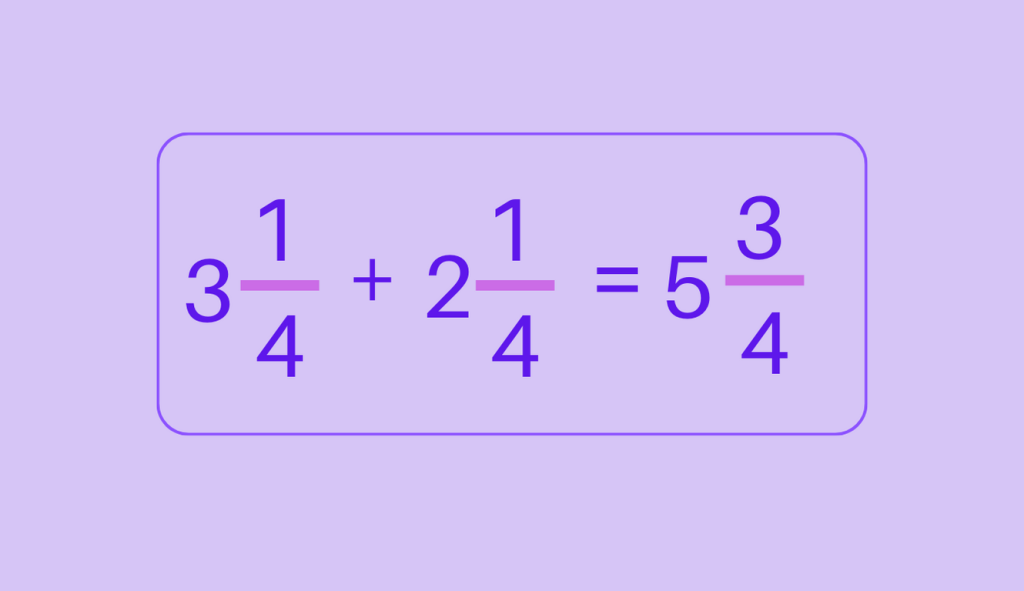
Adding Mixed Fractions with Unlike Denominators
In the case of mixed fractions with different denominators, the process involves finding a common denominator, converting the fractions, adding them, and simplifying the resulting sum.
Let’s say we want to add the following mixed fractions:
2\tfrac{1}{3} + 1\tfrac{2}{5}
Step 1: Convert the mixed fractions to improper fractions.
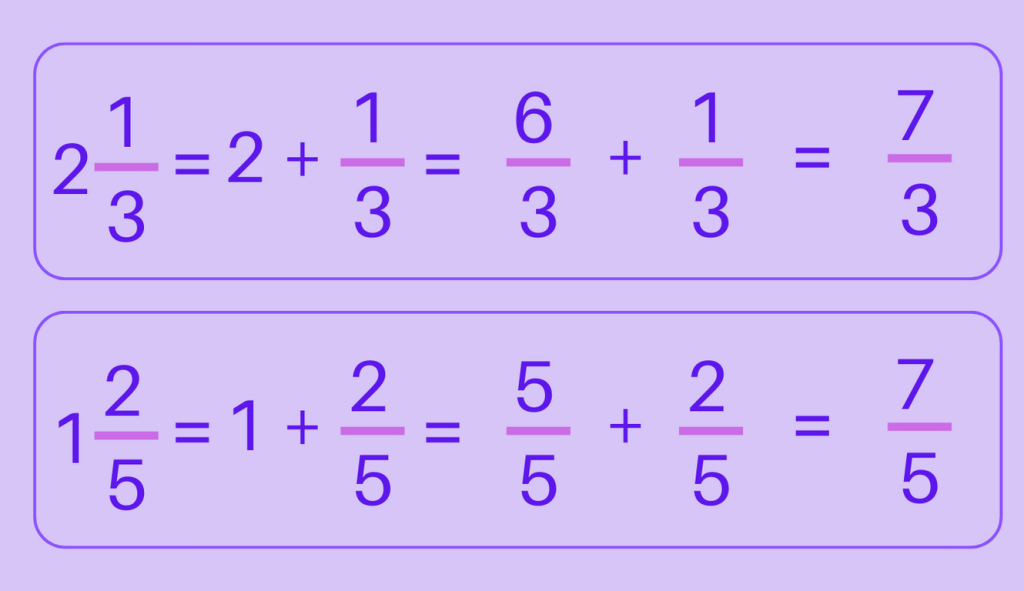
Step 2: Find a common denominator.
- To add fractions with unlike denominators, we need to find a common denominator. In this case, the least common multiple (LCM) of 3 and 5 is 15
Step 3: Rewrite the fractions with the common denominator and add them.
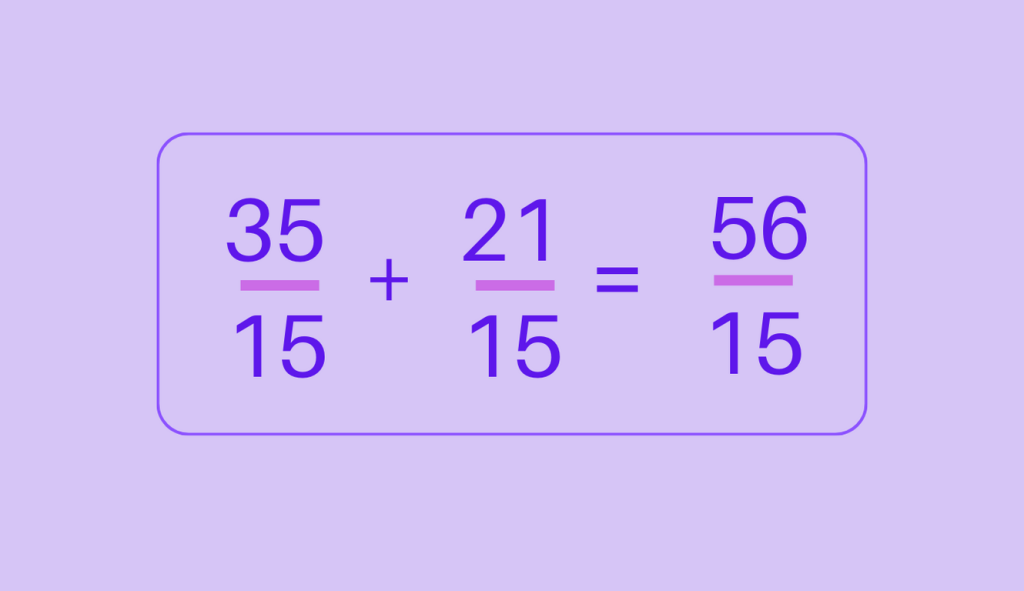
Step 5: Simplify (if necessary).
- The fraction can be expressed as a mixed fraction
Hence, the final answe will be:
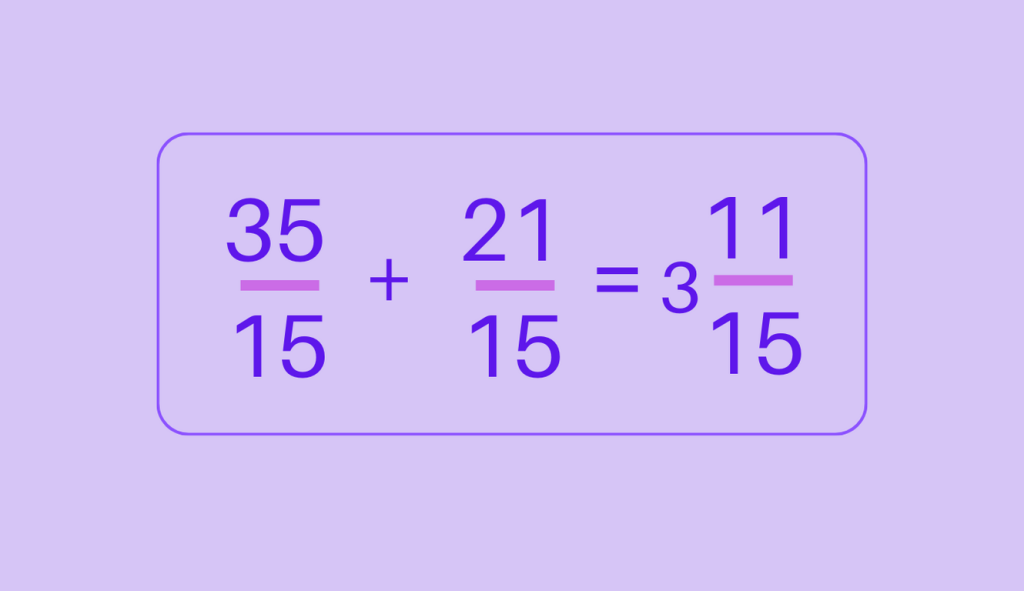
Examples
Adding Mixed Fractions with Like Denominators
1\tfrac{1}{4} + 2\tfrac{1}{4} = 3\tfrac{2}{4} = 3\tfrac{1}{2}
Adding Mixed Fractions with Unlike Denominators
3\tfrac{1}{2} + 2\tfrac{2}{3} = 3\tfrac{3}{6} = 5\tfrac{7}{6}
Quiz
Tips and Tricks
1. Convert to Improper Fractions
Tip: Before adding, convert the mixed numbers to improper fractions. To do this, multiply the whole number by the denominator, then add the numerator. The result becomes the new numerator, with the denominator remaining the same.
2. Add Whole Numbers Separately
Tip: Add the whole numbers separately from the fractions. This simplifies the process and helps avoid confusion. For exampls to add 5\tfrac{1}{3} and 4\tfrac{1}{3}, you can first add the whole number part, which is 5 and 4, which gives us 9, then we will add the fraction part, which gives us \frac{2}{3}, so our answer will be 9\tfrac{2}{3}
3. Add Fractions
Tip: Once you’ve added the whole numbers, add the fractions by finding a common denominator and then adding the numerators.
4. Simplify the Result
Tip: If possible, simplify the resulting fraction by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it.
Real life application
Story: “The Culinary Conundrum”
In a bustling kitchen, Chef Mia faced a culinary conundrum as she prepared a feast for a grand banquet. Her recipes called for adding mixed fractions of ingredients, presenting her with the challenge of accurately combining the quantities to create delectable dishes.
Challenge 1: The Bountiful Buffet
As Chef Mia crafted a bountiful buffet for the banquet, she needed to combine 2\tfrac{1}{3} cups of flour and 1\tfrac{2}{3} cups of sugar for a special cake recipe. By adding the mixed fractions with like denominators, she determined that a total of 4\tfrac{1}{3} cups of ingredients were required to create the perfect cake.
Challenge 2: The Festive Feast
For the main course, Chef Mia prepared a savory dish that called for 3\tfrac{1}{4}. As the banquet progressed, 2\tfrac{3}{4} pizzas remained. By adding the mixed fractions with like denominators, she calculated that a total of 5\tfrac{1}{4} pizzas had been enjoyed by the guests.
Challenge 3: The Sweet Finale
To conclude the banquet with a sweet finale, Chef Mia concocted a delightful dessert that demanded 4\tfrac{1}{2} cups of milk and 3\tfrac{1}{3} cups of cream. By adding the mixed fractions with unlike denominators, she ascertained that a total of 8\tfrac{5}{6} cups of dairy products were harmoniously blended to create the delectable dessert.
FAQ's
When adding mixed fractions with like denominators, simply add the whole numbers and the fractions while keeping the denominator unchanged. The resulting sum will be the combined quantity of the mixed fractions.
When adding mixed fractions with unlike denominators, the process involves finding a common denominator, converting the fractions, adding them, and simplifying the resulting sum to obtain the total quantity.
Simplifying the sum of mixed fractions ensures that the quantity is represented in its simplest form, making it easier to interpret and work with in subsequent calculations or real-life applications.
Adding mixed fractions is commonly used in cooking and baking recipes, construction and measurement tasks, and various other situations that involve combining quantities that include whole numbers and fractions.
The concept of adding mixed fractions can be extended to include subtracting, multiplying, and dividing mixed fractions, providing a comprehensive understanding of working with mixed quantities in mathematical operations.
Like? Share it with your friends
Facebook
Twitter
LinkedIn
