Area of a Parallelogram: Formula and Step-by-Step Method
Table of Contents
Introduction
Area of a Parallelogram
The area of a parallelogram is a fundamental concept in geometry, representing the total space enclosed within the boundaries of the parallelogram. Let’s delve into the formula and step-by-step method for calculating the area of a parallelogram and explore its significance in geometric calculations.
Analogy of Definition
Parallelogram Area Formula
The formula for finding the area of a parallelogram is A = base x height, where A represents the area, and the base and height are the respective measurements of the parallelogram. This formula provides a straightforward method for determining the enclosed space within a parallelogram.
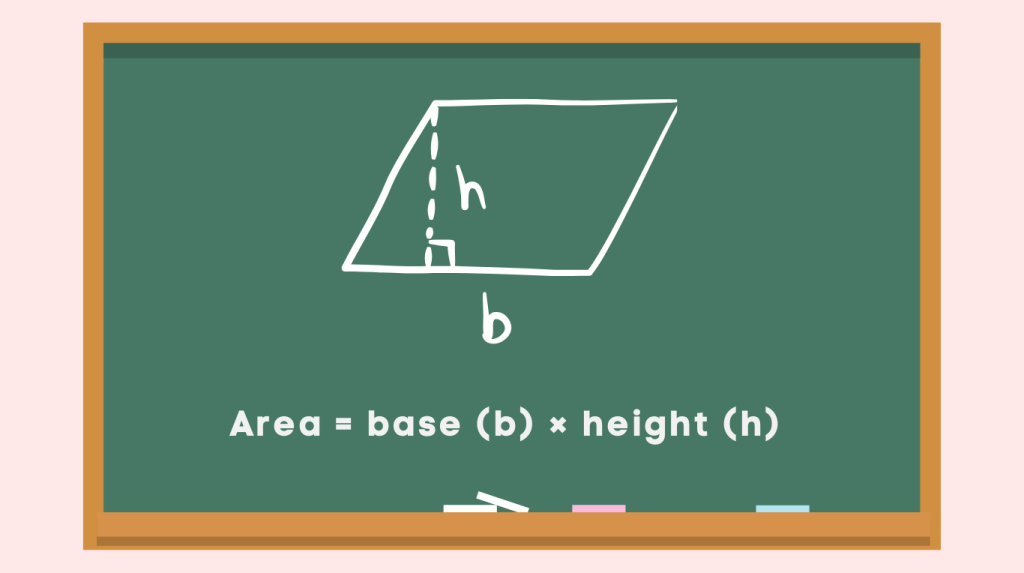
Method
Calculating the Area of a Parallelogram
To calculate the area of a parallelogram, one can utilize the formula A = base x height. Additionally, the method of dividing the parallelogram into triangles and calculating their individual areas can be employed to determine the total enclosed space.
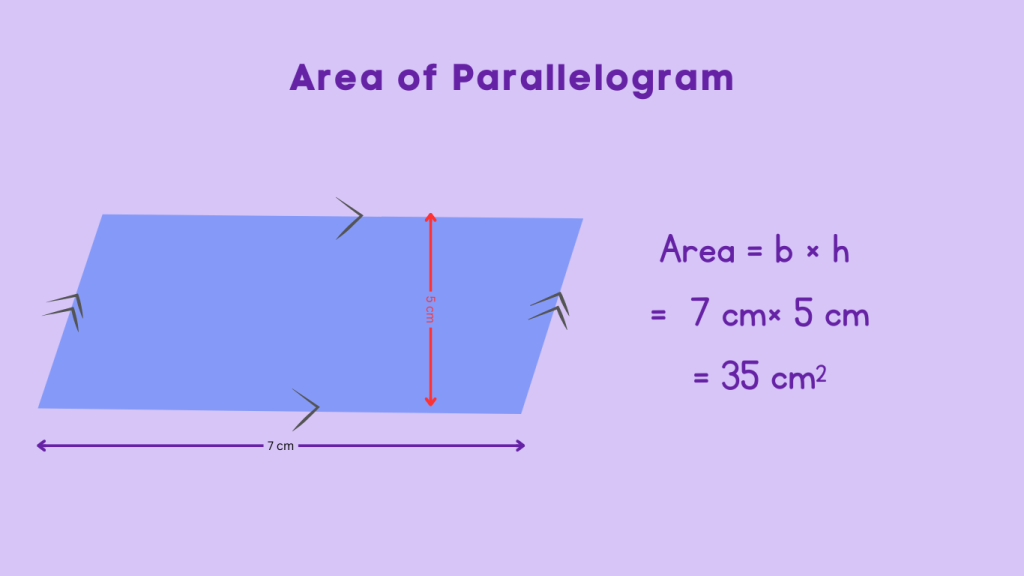
Examples
Example 1: Given a parallelogram with a base of 8 units and a height of 5 units, the area can be calculated using the formula A = base x height. Thus, A = 8 x 5 = 40 square units.
Example 2: If the base of a parallelogram measures 12 units and the height measures 6 units, the area can be determined as A = base x height, resulting in A = 12 x 6 = 72 square units.
Example 3: Consider a parallelogram with a base of 10 units and a height of 4 units. Applying the formula A = base x height yields A = 10 x 4 = 40 square units.
Summary::
These examples illustrate the step-by-step method of finding the area of a parallelogram using the formula A = base x height. By substituting the given measurements into the formula, the total enclosed space within the parallelogram can be calculated. This process demonstrates the practical application of the area of a parallelogram in determining spatial measurements and solving geometric problems.
These examples illustrate the step-by-step method of finding the area of a parallelogram using the formula A = base x height. By substituting the given measurements into the formula, the total enclosed space within the parallelogram can be calculated. This process demonstrates the practical application of the area of a parallelogram in determining spatial measurements and solving geometric problems.
Quiz
Tips and Tricks
1. Dividing the Parallelogram
Tip: To calculate the area, divide the parallelogram into two triangles and calculate their individual areas using the formula A = \frac{1}{2} x base x height.
2. Parallel Lines Property
Tip: Focus on the properties of parallel lines. Understanding that opposite sides are equal and parallel helps you see why the height is perpendicular to the base and how it affects the area.
3. Consider Diagonals
Tip: Think about how the diagonals of a parallelogram intersect and divide it into triangles. Visualizing these triangles can help you grasp the overall area better.
Real life application
Story: The Garden Design Challenge
A group of landscape designers faced the challenge of determining the area of a parallelogram-shaped garden to create an optimal landscaping plan.
Challenge 1: The Patio Project
The designers needed to calculate the area of the garden to determine the space available for constructing a patio. By measuring the base and height of the garden, they utilized the formula A = base x height to calculate the total area, enabling them to design an aesthetically pleasing patio layout.
Challenge 2: The Lawn Installation
To install a lush lawn in the garden, the designers required the precise area measurements. By applying the formula for the area of a parallelogram, they determined the total space available for the lawn, ensuring an efficient and visually appealing installation.
Challenge 3: The Pathway Planning
The designers aimed to create a winding pathway through the garden. By calculating the area of the parallelogram-shaped garden, they strategically planned the pathway layout, optimizing the use of space and enhancing the garden’s appeal.
FAQ's
The formula for finding the area of a parallelogram is A = base x height, where A represents the area, and the base and height are the respective measurements of the parallelogram.
The area of a parallelogram is directly related to its shape, as it represents the total space enclosed within the parallelogram’s boundaries.
Yes, the area of a parallelogram can be calculated using various methods, including the formula A = base x height, as well as the method of dividing the parallelogram into triangles and calculating their individual areas.
Understanding the area of a parallelogram is essential in real-life scenarios such as calculating the amount of flooring needed for a room, determining the space required for a garden, and optimizing the layout of furniture in a space.
In geometry, the concept of the area of a parallelogram is utilized to solve problems related to spatial measurements, determine the size of enclosed spaces, and analyze the dimensions of geometric figures.
Like? Share it with your friends
Facebook
Twitter
LinkedIn