Area of a Semi Circle: Formula and Examples
Table of Contents
Introduction
Area of a Semi Circle
The concept of the area of a semi circle plays a crucial role in geometry and mathematical calculations. Let’s delve into the formula and derivation of the area of a semi circle to gain a comprehensive understanding of this fundamental geometric concept.
Analogy of Definition
What is Area of a Semi Circle?
The area of a semi circle refers to the amount of space enclosed by the curved boundary of a semi circular shape. It is calculated using a specific formula derived from the area of a full circle, providing a means to quantify the space occupied by a semi circular region.
Method
Calculating the Area of a Semi Circle
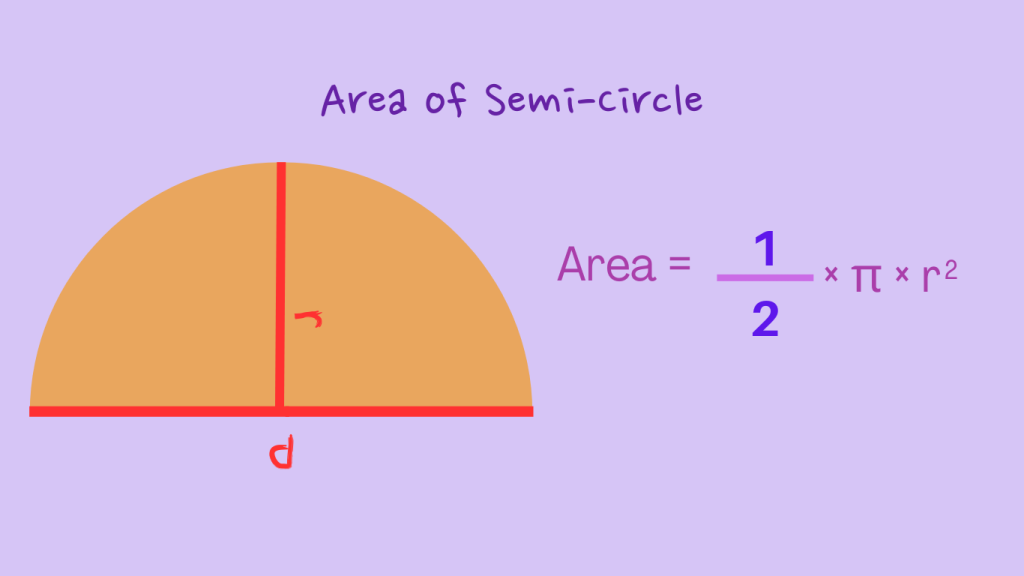
The area of a semi circle can be calculated using the formula A = (1/2) × π × r² , where π is a constant and r represents the radius of the semi circle. This formula allows for the precise determination of the area of a semi circular shape.
Examples
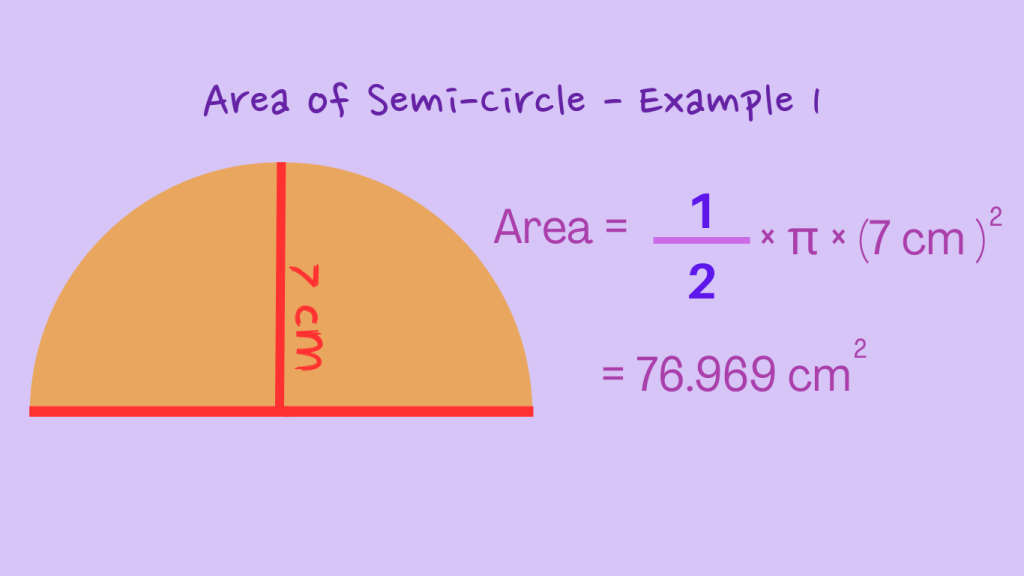
Example 1: Given the radius of a semi circle as 7 units, calculate the area of the semi circle.
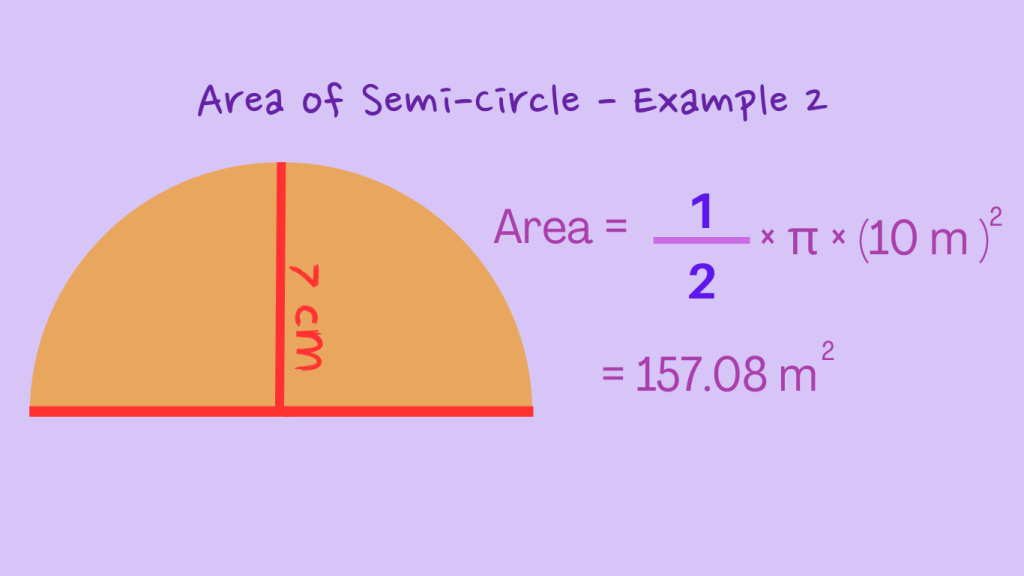
Example 2: If the radius of a semi circle is 10 meters, determine the area of the semi circle.
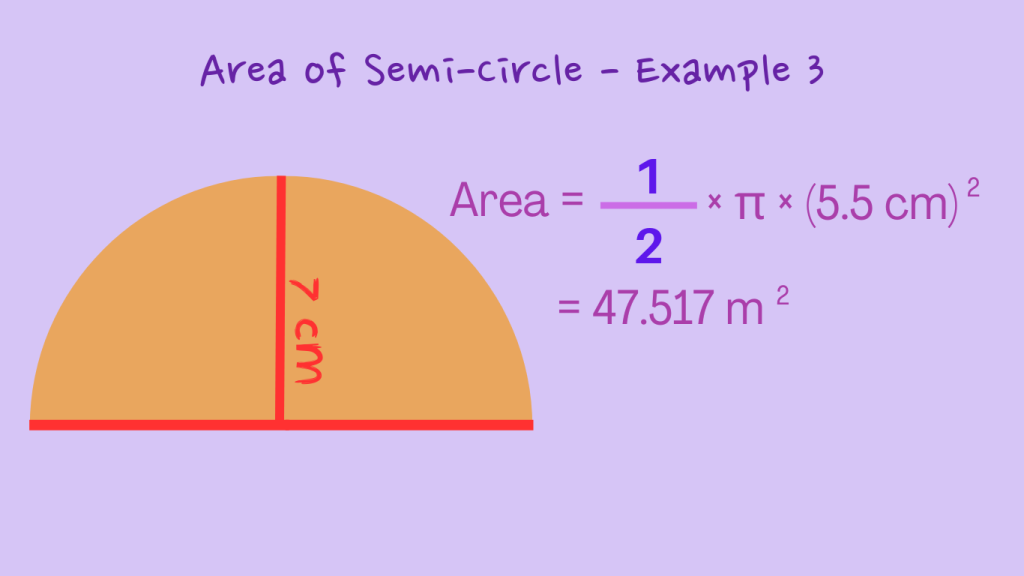
Example 3: Calculate the area of a semi circle with a radius of 5.5 centimeters.
Summary:
These examples illustrate the application of the formula for the area of a semi circle in calculating the space occupied by semi circular shapes. By substituting the given radius values into the formula A = (1/2) * π * r^2, the area of each semi circle is accurately determined, showcasing the practical use of the area formula in real-world scenarios.
These examples illustrate the application of the formula for the area of a semi circle in calculating the space occupied by semi circular shapes. By substituting the given radius values into the formula A = (1/2) * π * r^2, the area of each semi circle is accurately determined, showcasing the practical use of the area formula in real-world scenarios.
Quiz
Tips and Tricks
1. Understanding the Radius
Tip: When calculating the area of a semi circle, ensure that the radius value is squared and multiplied by the constant π to obtain the accurate area measurement.
2. Doubling for Full Circle Area
Tip: To find the area of a full circle, simply double the result obtained from the formula for the area of a semi circle.
3. Unit Conversion
Tip: When working with different units of measurement, ensure that the radius and resulting area are expressed in the same units for consistency and accuracy.
Real life application
Scenario: Architectural Design
Architects and designers frequently utilize the formula for the area of a semi circle in designing structures with semi circular elements, such as arches and domes. By accurately calculating the area of semi circular components, they can optimize space utilization and create aesthetically pleasing architectural features.
Scenario: Landscaping and Gardening
In landscaping and gardening, the area of a semi circle is employed to determine the space occupied by semi circular garden beds, pathways, and decorative elements. This allows landscapers to plan and allocate resources effectively, enhancing the visual appeal of outdoor spaces.
FAQ's
The formula for calculating the area of a semi circle is A = (1/2) × π × r², where π is a constant approximately equal to 3.14159 and r is the radius of the semi circle.
The formula for the area of a semi circle can be derived by considering the semi circle as half of a full circle. By using the formula for the area of a full circle, A = π * r^2, and dividing it by 2, we obtain the formula for the area of a semi circle, A = (1/2) * π * r^2.
The area of a semi circle is important in geometry as it allows us to calculate the space occupied by a semi circular shape, such as a half-moon or the base of a dome.
Yes, the formula for the area of a semi circle can be utilized to find the area of a full circle by simply doubling the result obtained from the formula for the area of a semi circle.
The area of a semi circle is directly related to the concept of pi (π) as the formula for the area of a semi circle, A = (1/2) * π * r^2, incorporates the value of π to calculate the area of the semi circle.
Like? Share it with your friends
Facebook
Twitter
LinkedIn