Understanding Cardinal Numbers with Examples
Table of Contents
Introduction
Cardinal Numbers
In the realm of mathematics, cardinal numbers play a crucial role in counting and quantifying objects or elements in a set. They are used to denote the quantity or number of items in a group, and understanding their properties is essential in various mathematical and real-world scenarios.
Analogy of Definition
What are Cardinal Numbers?
Cardinal numbers are a type of number used to represent the size or quantity of a set. They are used to answer the question “how many?” and are typically represented by numerals (e.g., 1, 2, 3, 4, etc.). Cardinal numbers are used for counting, ordering, and measuring the size of a set.
List of Cardinal Numbers
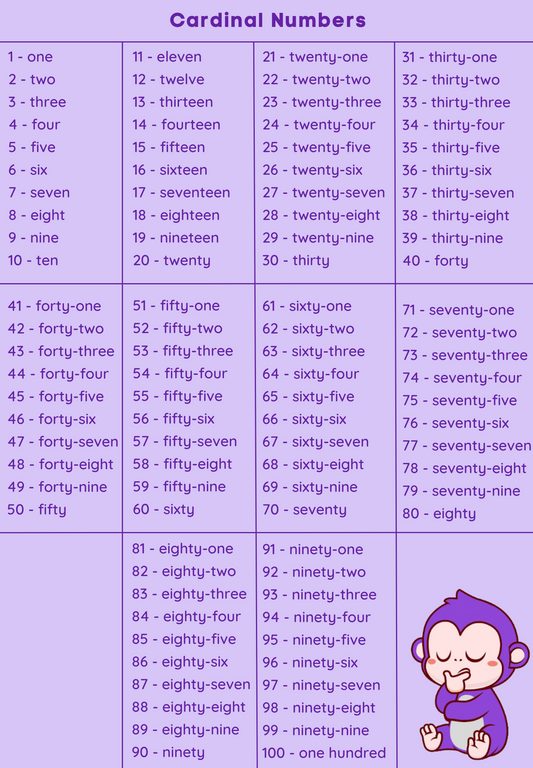
Method
Cardinal Numbers of Set
The cardinal number of a set refers to the number of elements or members in the set. It represents the size or quantity of the set and is denoted by a specific cardinal number. For example, if a set contains 5 elements, its cardinal number is 5. Cardinal numbers of sets are used in set theory, and other branches of mathematics to analyze and compare different sets.
When we talk about the cardinal number of a set, we’re essentially referring to the number of elements within that set.
For example, if we have a set Y = {2, 4, 6, 8, 10}, the cardinal number of set A is the count of elements it contains, which is 6. Therefore, we denote it as n(Y) = 6.
Cardinality
Cardinality is a concept closely related to cardinal numbers and refers to the measure of the “size” of a set. It represents the number of elements in a set and is used to compare the sizes of different sets. Cardinality is a fundamental concept in set theory and is essential in understanding the properties and relationships between sets. For example there is a set of 10 fruits, then the cardinality will be 10.
Differences between Cardinal and Ordinal Numbers
Cardinal numbers represent the quantity or size of a set, while ordinal numbers represent the position or order of elements in a sequence. For example, “3” is a cardinal number representing the quantity of items in a set, while “3rd” is an ordinal number representing the position of an item in a sequence. Understanding the distinction between cardinal and ordinal numbers is crucial in various mathematical.
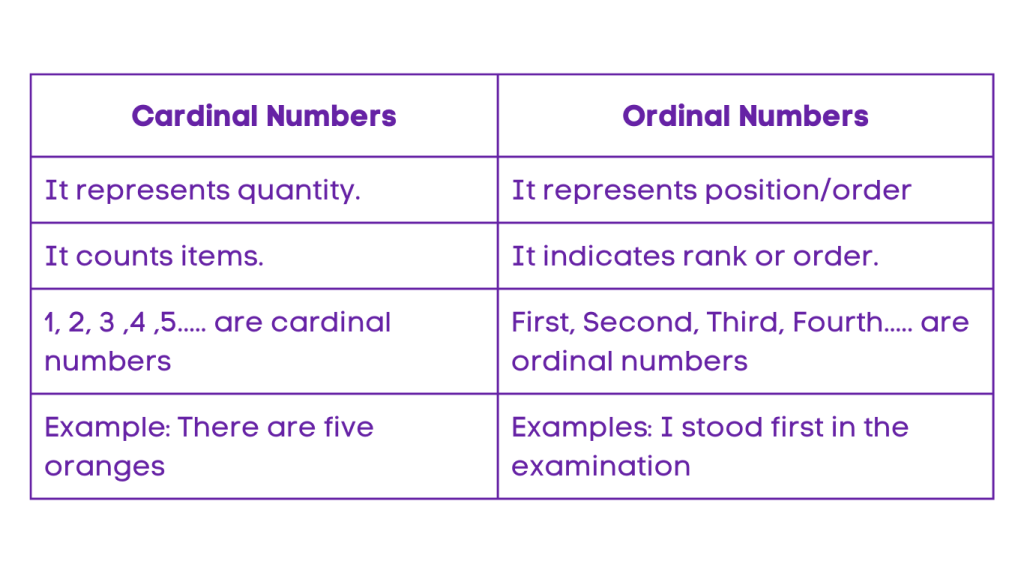
Examples
Example 1: There is one apple on the table.
Example 2: She has two cats as pets.
Example 3: We need three more chairs for the meeting.
Example 4: He scored four goals in the game yesterday.
Quiz
Tips and Tricks
1. Start with the Basics
Tip: Begin by understanding the concept of cardinality as the measure of the “size” of a set, which represents the number of elements in the set.
2. Use Concrete Examples
Tip: Work with physical objects like toys, blocks, or beads to demonstrate cardinality. Counting real objects can make the concept more tangible.
3. Practice Counting
Tip: Regularly practice counting objects, starting from small sets and gradually increasing the complexity. This helps reinforce the idea of cardinality.
4. Learn Number Words
Tip: Memorize number words from one to ten, and then progress to higher numbers. This helps in recognizing and using cardinal numbers in everyday language.
5. Practice Ordering
Tip:Arrange objects in order from smallest to largest or vice versa. This reinforces the concept of ordinal numbers, which are closely related to cardinal numbers.
Real life application
Story: “The Cardinal Numbers Adventure of Emma and Liam”
Emma and Liam, two young explorers, embarked on a journey filled with numerical challenges that required them to apply their knowledge of cardinal numbers in real-life situations.
Challenge 1: The Treasure Hunt
Emma and Liam discovered a treasure map with a series of numerical clues. The map indicated that they needed to find a chest hidden in a location with 100 trees. Using their understanding of cardinal numbers, they counted the trees and successfully located the treasure chest.
Challenge 2: The Puzzle Maze
In a mysterious maze, Emma and Liam encountered a series of doors labeled with cardinal numbers. To navigate through the maze, they had to open the doors in ascending order, starting from 1. Their knowledge of cardinal numbers helped them identify the correct sequence and find their way out of the maze.
Challenge 3: The Magical Garden
In a magical garden, Emma and Liam were tasked with counting the flowers in different sections and determining the total cardinality of the garden. By applying their understanding of cardinal numbers and cardinality, they accurately calculated the number of flowers and completed their adventure successfully.
FAQ's
Cardinal numbers are essential in mathematics for counting, measuring, and representing the quantity or size of sets. They form the basis for numerical operations, comparisons, and calculations in various mathematical fields.
Cardinal numbers represent the quantity or size of a set, while ordinal numbers represent the position or order of elements in a sequence. Cardinal numbers answer the question “how many?” while ordinal numbers indicate “which in order?”
Cardinal numbers are used in everyday scenarios such as counting objects, measuring quantities, and expressing numerical values. They are applied in fields such as finance, statistics, engineering, and data analysis.
In set theory, cardinal numbers are used to determine the size or cardinality of sets. They help in comparing the sizes of different sets and analyzing the relationships between sets.
In data analysis and statistics, cardinal numbers are used to quantify and categorize data. They help in identifying the number of observations, measuring frequencies, and organizing data into meaningful sets for analysis and interpretation.
Like? Share it with your friends
Facebook
Twitter
LinkedIn