Commutative Property – Definition and Examples
Table of Contents
Introduction
Commutative Property
In the realm of mathematics, the commutative property plays a significant role in understanding the behavior of operations such as addition and multiplication. This property has practical applications in various mathematical concepts and problem-solving scenarios. Let’s delve into the world of the commutative property and explore its implications.
Analogy of Definition
What is Commutative Property?
The commutative property refers to the principle that the order of the numbers does not affect the result when performing addition or multiplication. In simpler terms, it means that changing the order of the numbers being added or multiplied does not change the sum or product.
Method
Commutative Property of Addition
When applying the commutative property to addition, it means that the sum of two or more numbers remains the same regardless of the order in which the numbers are added. For example, 3 + 5 is equal to
5 + 3, demonstrating the commutative property in action.
Commutative Property of Multiplication
Similarly, the commutative property applies to multiplication, indicating that the product of two or more numbers remains unchanged regardless of the order in which the numbers are multiplied. For
instance, 2 x 4 is equal to 4 x 2, showcasing the commutative property at work.
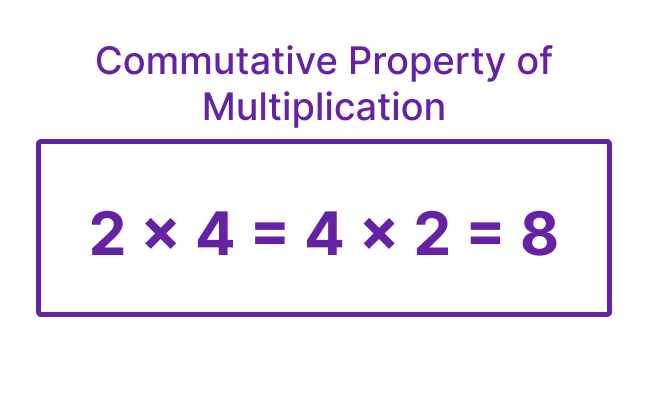
Why Commutative Property Doesn’t Work on Division and Subtraction ?
It is important to note that the commutative property does not hold true for division and subtraction. Unlike addition and multiplication, the order of numbers does affect the result when performing division and subtraction. For example, 5 – 3 is not equal to 3 – 5, and 10 ÷ 2 is not equal to 2 ÷ 10, highlighting the limitations of the commutative property in these operations.
Examples
Example 1: Addition
3 + 7 = 7 + 3 = 10
The commutative property holds true for addition, as the sum remains the same regardless of the order of the numbers.
Example 2: Multiplication
4 x 6 = 6 x 4 = 24
The commutative property is evident in multiplication, as the product remains unchanged when the order of the numbers is switched.
Quiz
Tips and Tricks
1.Understanding the Commutative Property
Tip: The commutative property states that the order of numbers being added or multiplied does not change the result. In other words, you can swap the order of the numbers without affecting the outcome.
2.Visualize Swapping
Tip: Imagine moving the numbers around within an addition or multiplication problem. If the result stays the same, then you’re applying the commutative property correctly.
3.Apply to Addition
Tip: For addition, the commutative property means that you can add the numbers in any order and still get the same sum. For example,
4.Apply to Multiplication
Tip: Similarly, the commutative property applies to multiplication, allowing you to multiply numbers in any order and still get the same product. For example,
Real life application
Story: “The Math Magic Show withh Commutative Property”
Join us on a magical journey where the commutative property of addition and multiplication comes to life in various real-life scenarios.
Scenario 1: The Birthday Party
At a birthday party, the children were given 3 balloons each, and there were 5 children in total. The commutative property of addition allowed the host to calculate the total number of balloons by adding 3 balloons 5 times or 5 balloons 3 times, resulting in 15 balloons.
Scenario 2: The Art Class
In an art class, the students were creating patterns using colored beads. The commutative property of multiplication enabled the students to determine the total number of beads needed for a pattern by multiplying the number of beads in each row by the number of rows, regardless of the order.
FAQ's
The commutative property is significant in simplifying calculations and understanding the behavior of addition and multiplication. It provides a fundamental principle that allows for efficient manipulation of numbers in various mathematical operations and real-life scenarios.
The commutative property does not apply to division and subtraction because the order of numbers does affect the result in these operations. Unlike addition and multiplication, changing the order of numbers in division and subtraction leads to different outcomes.
The commutative property has practical applications in everyday scenarios, such as calculating the total cost of items, determining the number of objects in a collection, and creating patterns or arrangements. It simplifies calculations and provides a systematic approach to solving problems.
Yes, the commutative property is often used to simplify complex expressions by rearranging the order of terms in addition and multiplication. This simplification aids in solving equations, evaluating algebraic expressions, and performing arithmetic operations more efficiently.
Yes, the commutative property can be demonstrated through various examples, quizzes, and real-life applications to illustrate its practical implications and limitations. By showcasing the behavior of addition and multiplication, the commutative property can be effectively conveyed in different contexts.
Like? Share it with your friends
Facebook
Twitter
LinkedIn