Composite Number – Meaning, Examples and List of Composite Numbers
Table of Contents
Introduction
Composite Numbers
In the realm of mathematics, numbers play a crucial role in various calculations and problem-solving. One important category of numbers is known as composite numbers. These numbers have unique properties and are distinct from prime numbers. Let’s explore the world of composite numbers and understand their significance in mathematical concepts.
Analogy of Definition
What are Composite Numbers?
Composite numbers are positive integers greater than 1 that have more than two distinct positive divisors. In simpler terms, these numbers can be divided evenly by at least one other number besides 1 and themselves. For example, 4 is a composite number because it can be divided by 1, 2, and 4.
Properties of Composite Number
Composite numbers have several distinct properties that set them apart from prime numbers. Some of the key properties include:
- Composite numbers have more than two factors, including 1 and the number itself.
- They can be expressed as the product of two or more positive integers.
- Composite numbers are not divisible only by 1 and themselves, unlike prime numbers.
- They can be decomposed into prime factors, which helps in understanding their structure and properties.
List of Composite Numbers
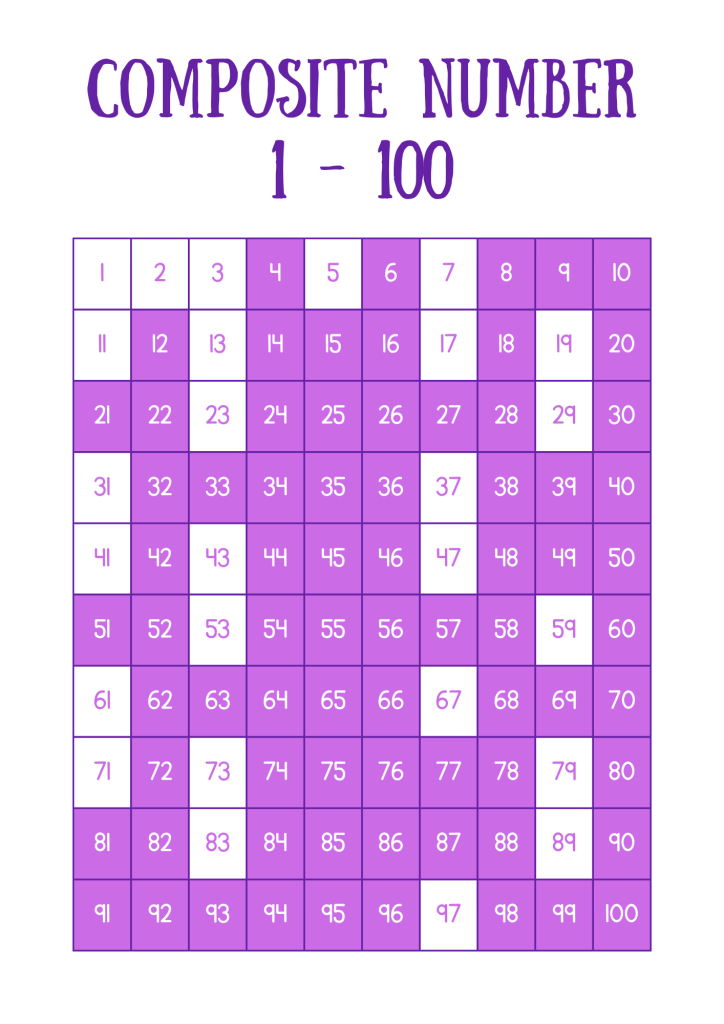
Method
Finding Composite Numbers
To identify composite numbers, you can follow a simple method. Start by listing the factors of a given number. If the number has more than two factors, it is a composite number. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12, indicating that 12 is a composite number.
Prime vs. Composite Numbers
The key difference between prime and composite numbers lies in their factors. Prime numbers have only two distinct positive divisors: 1 and the number itself. In contrast, composite numbers have more than two factors, making them divisible by numbers other than 1 and themselves. Prime numbers are the building blocks of all numbers, while composite numbers are formed by multiplying prime numbers together.
Types of Composite Numbers
Composite numbers can be further classified based on their properties and factors. Some of the common types of composite numbers include:
Even Composite Numbers
These are composite numbers that are divisible by 2. All the even numbers which aren’t prime numbers are composite numbers.
Odd Composite Numbers
These composite numbers are not divisible by 2 and usually have an odd number of factors. All the even numbers which aren’t prime numbers are composite numbers.
Examples
Let’s explore some examples of composite numbers and understand their properties:
Quiz
Tips and Tricks
1. Know the Multiplication Table
Tip: Composite numbers are those that have more than two factors. By familiarizing yourself with the multiplication table, you can easily identify composite numbers by recognizing which numbers have multiple factors.
2. Look for Repeated Multiplication
Tip: When trying to determine if a number is composite, look for patterns of repeated multiplication. If a number can be divided evenly by numbers other than 1 and itself, it is composite.
3. Identify Prime Factors
Tip: Break down larger numbers into their prime factors. If a number has prime factors other than 1 and itself, it is composite.
4. Use Visual Aids
Tip: Draw arrays or use manipulatives to represent numbers and their factors. This visual representation can help in understanding composite numbers by seeing how they can be divided into smaller equal parts.
5. Practice with Examples
Tip: Work through examples of composite numbers together, identifying their factors and discussing how they can be divided. This hands-on practice reinforces understanding and recognition of composite numbers.
Real life application
Story: “The Composite Number Quest”
In a world filled with mathematical mysteries, a group of young adventurers set out on a quest to explore the properties and applications of composite numbers.
Challenge 1: The Puzzle Palace
The adventurers encountered a magical puzzle palace where they had to solve riddles related to composite numbers. One of the challenges required them to identify the composite number among a set of options. By applying their knowledge of factors and divisibility, they successfully completed the challenge.
Challenge 2: The Enchanted Garden
As they journeyed through an enchanted garden, the adventurers encountered unique plants with a specific number of petals. They used their understanding of composite numbers to determine the factors of the petal counts and classify the plants accordingly. This helped them navigate through the garden and appreciate the mathematical beauty of nature.
Challenge 3: The Timeless Clock Tower
In the final challenge, the adventurers faced a timeless clock tower that displayed composite numbers as part of its intricate design. By recognizing the patterns and properties of composite numbers, they deciphered the hidden messages within the clock tower and unveiled its secrets.
FAQ's
Composite numbers have more than two factors, can be expressed as the product of two or more positive integers, and are not divisible only by 1 and themselves. They can also be decomposed into prime factors, revealing their unique structure.
Composite numbers can be identified by listing their factors and checking if they have more than two distinct positive divisors. If a number has more than two factors, it is a composite number.
The key difference lies in their factors. Prime numbers have only two distinct positive divisors, while composite numbers have more than two factors. Prime numbers are the building blocks of all numbers, while composite numbers are formed by multiplying prime numbers together.
Yes, composite numbers can be classified based on their properties and factors. Some common types include even composite numbers, odd composite numbers, and perfect composite numbers.
Composite numbers have practical applications in various fields, including cryptography, computer science, and number theory. They are used in encryption algorithms, factorization methods, and mathematical modeling, making them essential in problem-solving and data security.
Like? Share it with your friends
Facebook
Twitter
LinkedIn