Exponents – Definition, Properties of Exponents & Examples
Table of Contents
Introduction
What are Exponents?
Exponents are a fundamental concept in mathematics that represent repeated multiplication of a number by itself. They are denoted by a small number written above and to the right of a base number, which indicates the number of times the base is multiplied by itself.
Analogy of Definition
The Symbol of Exponents
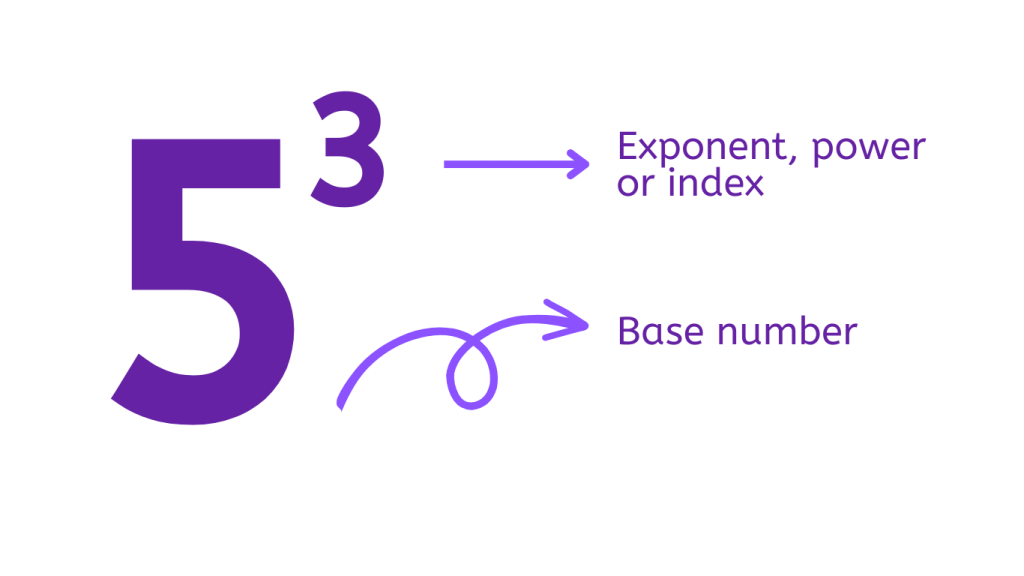
The symbol used to represent exponents is called a caret or a superscript. It is written as a small number placed above and to the right of the base number. For example, in the expression 53, 5 is the base, and 3 is the exponent. It is read as 5 to the power 3.
Method
Properties of Exponents
Exponents follow several properties or laws that govern their behavior in mathematical operations. These properties include the Law of Product, Law of Quotient, Law of Zero, Law of Negative Exponent, Law of Power of a Power, Law of Power of a Product, and Law of Power of a Quotient.
Properties can further be explained as:
Law of Product: ax * ay = ax+y
Law of Quotient: ax/ay = ax-y
Law of Zero:a0 = 1
Law of Negative Exponent:a-x = 1/ax
Law of Power of a Power:(ax)y = axy
Law of Power of a Product:(ab)x = axbx
Law of Power or a Quotient:(a/b)x = ax/bx
Examples
Using the Laws of Exponent
Example 1: Laws of Product 52 * 53
According to the Law of Product, when multiplying two powers with the same base, you add the exponents.
52 * 53 = 5(2+3) = 55
So, 52 * 53 = 55
Quiz
Tips and Tricks
1.Power of One Rule
Tip: Any number raised to the power of 1 equals itself. For example, a1.
2.Power of a Fraction Rule
Tip: A fraction as an exponent represents taking the root of a number. For instance, a1/n =\sqrt[n]{a}
3.Increasing Powers
When the exponent increases, the result gets larger. For instance, 23 is greater than 22 as 23 is 8 and 22 is 4.
4.Decreasing Powers
When the exponent decreases, the result gets smaller. For example, 21 is smaller than 22 as 21 is 1 and 22 is 4
For more trips and tricks, visit our site ChimpVine and make learning enjoyable.
Real life application
Story: “The Exponent Adventures of Emma and Ethan”
Emma and Ethan, two curious students, embarked on a journey to explore the real-life applications of exponents and their properties.
Application 1: The Growth of Bacteria
Emma and Ethan visited a biology lab where they learned about the rapid growth of bacteria. The number of bacteria doubled every hour. Using the Law of Power of a Power, they calculated the total number of bacteria after 5 hours, which was 2^5 or 32 times the initial amount.
Application 2: Financial Investments
In a finance workshop, Emma and Ethan discovered the concept of compound interest. They used the Law of Power of a Power to calculate the future value of an investment by raising the growth rate to the power of the number of years.
Application 3: Scientific Notation
During a physics demonstration, Emma and Ethan encountered large numbers in scientific notation. They applied the Law of Power of a Product to simplify the expressions and perform calculations efficiently.
Application 4: Electrical Engineering
In an engineering lab, Emma and Ethan learned about electrical circuits and the concept of resistance. They used the Law of Negative Exponent to represent resistance values in terms of reciprocal powers.
Application 5: Population Growth
Emma and Ethan explored the impact of population growth on resources and the environment. They used the Law of Quotient to calculate the rate of population increase or decrease over time.
FAQ's
Understanding the properties of exponents is crucial for simplifying expressions, solving equations, and performing calculations involving repeated multiplication. These properties provide a systematic approach to handling exponents in various mathematical scenarios.
The Law of Zero states that any non-zero number raised to the power of zero is equal to 1. This property is essential in simplifying expressions and handling special cases involving exponents.
The Law of Negative Exponent allows us to represent reciprocals of numbers raised to positive exponents. It is used to simplify expressions and perform calculations involving negative exponents.
The properties of exponents have practical applications in various fields, including science, finance, engineering, and population studies. They are used to model growth, calculate values, and simplify complex expressions in real-world scenarios.
Yes, the Law of Power of a Power allows us to simplify expressions by multiplying the exponents of powers raised to another power. This property is useful in handling complex calculations and representing quantities in a concise form.
Like? Share it with your friends
Facebook
Twitter
LinkedIn