How to Convert Fraction to Percent? – Step-by-Step Method
Table of Contents
Introduction
Fraction to Percent Conversion
Converting fractions to percentage is a fundamental concept in mathematics and everyday life. It involves transforming fractional values into their equivalent percentage representation, allowing for easier comparison and analysis of data.
Analogy of Definition
How to Convert Fraction to Percent?
Converting a fraction to a percentage involves determining the equivalent percentage value of a given fraction. This process enables the representation of fractional quantities in percentage form, providing a clearer understanding of the data.
Method
Step-by-Step Method
The process of converting fractions to percent can be achieved by dividing the numerator by the denominator, then multiplying the result by 100 to obtain the percentage value.
Step 1: Divide the Numerator by the Denominator
Start by dividing the top number (numerator) of the fraction by the bottom number (denominator). This will give you a decimal number.
Let’s convert \frac{3}{4} to percent.
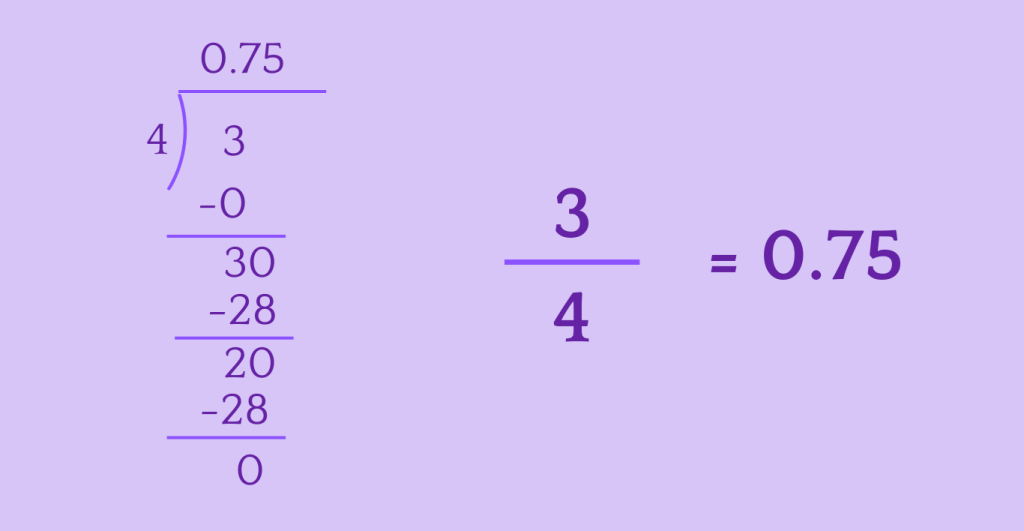
Step 2: Multiply by 100
Once you have the decimal result from step 1, multiply it by 100 to convert it to a percentage.
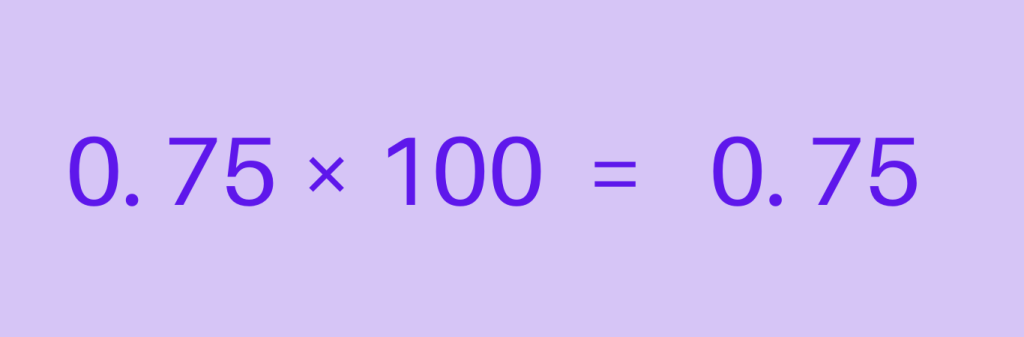
Step 3: Add the Percent Symbol
Finally, add the percent symbol (%) to the result to indicate that it is a percentage.
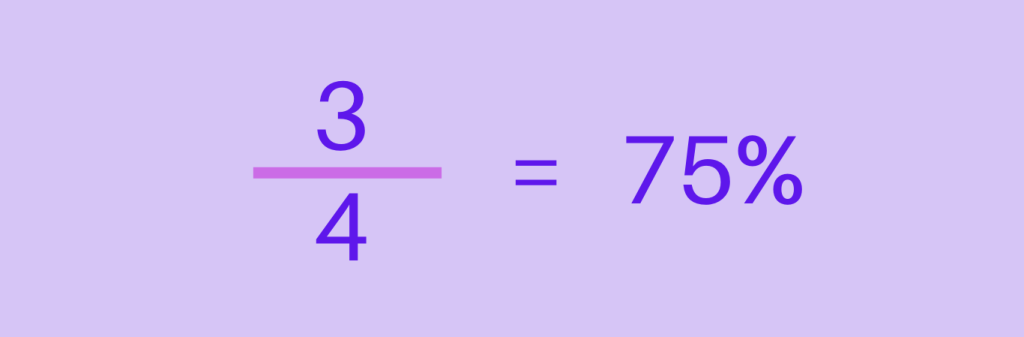
Examples
Example 1: Convert \frac{1}{2} to a Percentage
Step 1: \frac{1}{2} = 0.5
Step 2: 0.5 × 100 = 50
Step 3: \frac{1}{2} = 50%
Example 2: Convert \frac{2}{5} to a Percentage
Step 1: \frac{2}{5} = 0.4
Step 2: 0.4 × 100 = 40
Step 3: \frac{2}{5} = 40%
Summary::
This example demonstrates the step-by-step process of converting the fraction 3/4 to a percentage. By dividing the numerator by the denominator and multiplying the result by 100, the equivalent percentage value of 75% is obtained. This method illustrates the conversion of fractional quantities to their percentage representation, facilitating easy comparison and analysis of values.
This example demonstrates the step-by-step process of converting the fraction 3/4 to a percentage. By dividing the numerator by the denominator and multiplying the result by 100, the equivalent percentage value of 75% is obtained. This method illustrates the conversion of fractional quantities to their percentage representation, facilitating easy comparison and analysis of values.
Quiz
Tips and Tricks
1. Understanding Equivalent Fractions
Tip: To convert a fraction to a percent, divide the numerator by the denominator and multiply by 100.
2. Calculating Discounts
Tip: Convert the fraction to a percentto determine the discount percentage.
3. Understanding Proportions
Tip: Use the formula (Numerator / Denominator) * 100 to convert the fraction to percent.
Real life application
Story: The Shopping Spree Challenge
Emily and Alex embarked on a shopping spree, armed with the knowledge of converting fraction to percent o make informed purchasing decisions.
Challenge 1: Calculating Discounts
Emily spotted a dress on sale for 3/4 of its original price. By converting the fraction to percent, she determined that the discount was 75%, allowing her to make a well-informed purchase.
Challenge 2: Understanding Proportions
Alex needed to adjust a recipe that called for 1/3 cup of sugar. By converting the fraction to percent, he realized that 1/3 was equivalent to 33.33%, enabling him to proportionally adjust the recipe for his needs.
Challenge 3: Calculating Interest Rates
In a financial decision, Emily needed to calculate the interest rate on a loan represented by the fraction 5/8. By converting the fraction to percent, she determined that the interest rate was 62.5%, aiding her in making an informed financial choice.
FAQ's
Converting fractions to percentages is important as it allows for easy comparison and understanding of values in different formats. It also helps in real-life situations such as calculating discounts and understanding proportions.
To convert a fraction to a percentage, you can divide the numerator by the denominator, then multiply the result by 100 to get the percentage value.
Yes, all fractions can be converted to percentages using the appropriate formula and method.
The formula for converting a fraction to a percentage is (Numerator / Denominator) * 100.
The concept of converting fractions to percentages is applied in various real-life scenarios such as calculating interest rates, understanding test scores, and determining proportions in recipes.
Like? Share it with your friends
Facebook
Twitter
LinkedIn