How To Do Long Division? – Steps and Methods
Table of Contents
Introduction
Understanding Division
Division is a fundamental operation in mathematics that involves the distribution of a quantity into equal parts. It is the process of splitting a number into equal groups or determining how many times one number is contained within another. In this article, we will explore the concept of division, division properties, and the method of long division.
Analogy of Definition
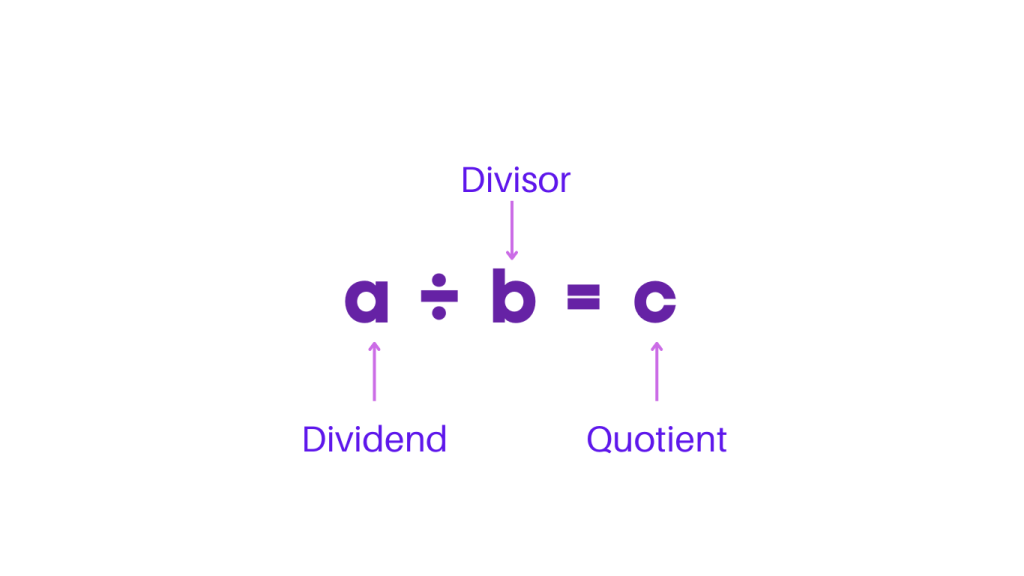
The Division Equation
The division equation is represented as a ÷ b = c, where ‘a’ is the dividend, ‘b’ is the divisor, and ‘c’ is the quotient. The dividend is the number being divided, the divisor is the number by which the dividend is divided, and the quotient is the result of the division. When the number isn’t excatly divisor, there may be a remainder as well. It is the number that cannit be further divided.
Method
How to Do Long Division
Division is one of the four basic mathematical operations which includes addition, subtraction, and multiplication. Long division is a method used to divide large numbers or polynomials by hand. The process involves several steps, including dividing, multiplying, subtracting, and bringing down digits. It is a systematic approach to division that allows for the accurate calculation of the quotient and remainder.
Steps of Doing Long Division
Step 1: Set up the division problem.
Step 2: Divide the first digit of the dividend by the divisor and write the answer on the top which will be the quotient.
Step 3: Subtract the result from the number and write down the difference,
Step 4: Bring down the next digit of the dividend
Step 5: Repeat the same process until it can’t be furter divided.
Let’s look at some examples.
Examples
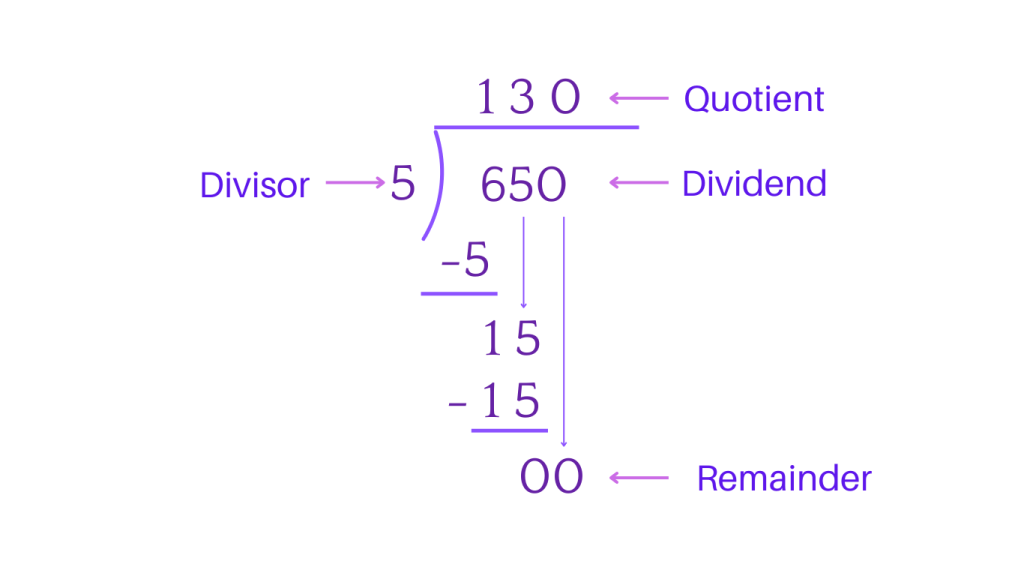
Example 1: Long Division without remainder
Dividing 650 by 5
Step 1: Setting up the division problem
Step 2: Divide the first digit 6, by 5 . As 6 cannot be divided by 5, we will look for a number less than 6 that 5 can divide, which is 5 itself. So, 5 ÷ 5 = 1, we will write 1 in the quotient.
Step 3: Subtract 6 – 5 = 1.
Step 4: We bring down the next digit of the dividen wihch is 5. The new dividend will be 15, we can divide 15 by 5 with quotient 3, as 5 * 3 = 15.
Step 5: Subtract 15 – 15 =0, we will bring the next digit down, which is 0.
Step 6: As 5 ÷ 0 = 0, we will now divide the dividend of 0 by 0, which will give us 0, so our answer will be 130.
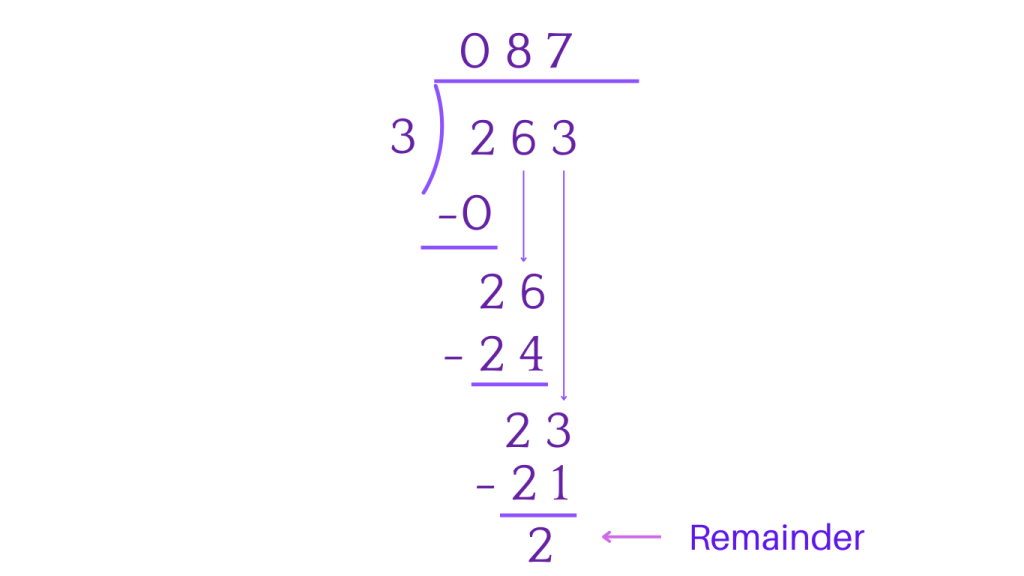
Example 2: Long Division with Remainder
Divide 263 by 3
Step 1: Setting up the division problem
Step 2: Divide the first digit 2, by 3 . As 3 is greater than 2, we will put 0 and bring the next digit down.
Step 3: Then, 26 will be the dividend. We can’t divide 26 by 3, however we know that 3*8 = 24, so we will use 8 as the quotient.
Step 4: Subtract 26 – 24 = 2. Bring down 3, so the next dividend will be 23.
Step 5: We can’t divide 23 by 3, but 7 * 3 = 21, so we will use 7 as the quotient.
Step 6: Subtract 23 – 21 = 2, there is no othher digit, so 2 is our remainder and we cannot go further.
Learn division with interactive activities on our site ChimpVine.
Quiz
Tips and Tricks
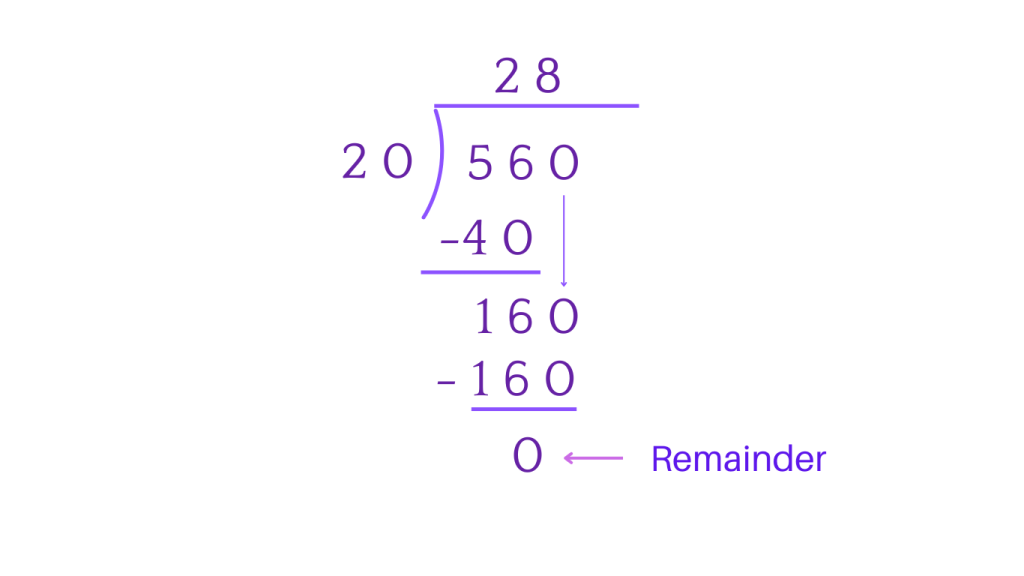
1. Long Division for Two Digits
Tip: If the divisor is a two digit number, we will look for the first two digit of the dividend and carry out the division.
2. Dividing with 0
Tip: If 0 is divided by any number, the answer will be 0. For example, 0 ÷55 = 0
3. Dividing with 1
Tip: If any number is divided by 1, the quotient will be the same number. For example, 40 ÷1=40
4. Division Formula
Tip: We can use the division formula to verify quotient and remainder. The formula is Dividend = (Divisor * Quotient) + Remainder.
Real life application
Story: “The Long Division Adventures of Sam and Emma”
Sam and Emma were two curious explorers who encountered real-life situations where the concept of long division played a crucial role in solving problems and making decisions.
Challenge 1: The Recipe Dilemma
Sam and Emma were passionate about cooking and decided to bake a batch of cookies. The recipe called for 2 cups of flour, and they needed to divide the flour equally into 4 portions. By using the division equation, they determined that each portion should contain 0.5 cups of flour, ensuring the perfect consistency for their cookies.
Challenge 2: The Budgeting Puzzle
As they planned a road trip, Sam and Emma needed to divide their total budget of $500 over 5 days of travel. By applying the division equation, they calculated that they could spend $100 per day, allowing them to manage their expenses effectively and enjoy their journey without overspending.
Challenge 3: The Party Planning Adventure
Sam and Emma had to divide 60 party favors into 6 equal groups for their friend’s birthday party. Using the concept of division, they determined that each group would receive 10 party favors, ensuring that all the guests had an equal share of the fun.
FAQ's
Like? Share it with your friends

