How to Find Circumference? – Formula with Example
Table of Contents
Introduction
Circumference of Circle
The concept of circumference plays a fundamental role in geometry and mathematics, particularly when dealing with circular shapes. Let’s delve into the formula for finding the circumference of a circle and explore its significance in solving mathematical problems and real-world applications.
Analogy of Definition
Elements of Circumference
The circumference of a circle is the distance around the circle’s edge or boundary. It is a fundamental concept in geometry and has several key elements that are essential for understanding and calculating it.
Center
The center of a circle is a fixed point from which every point on the circle is equidistant. This distance is known as the radius. The center is often denoted by the letter “O”.
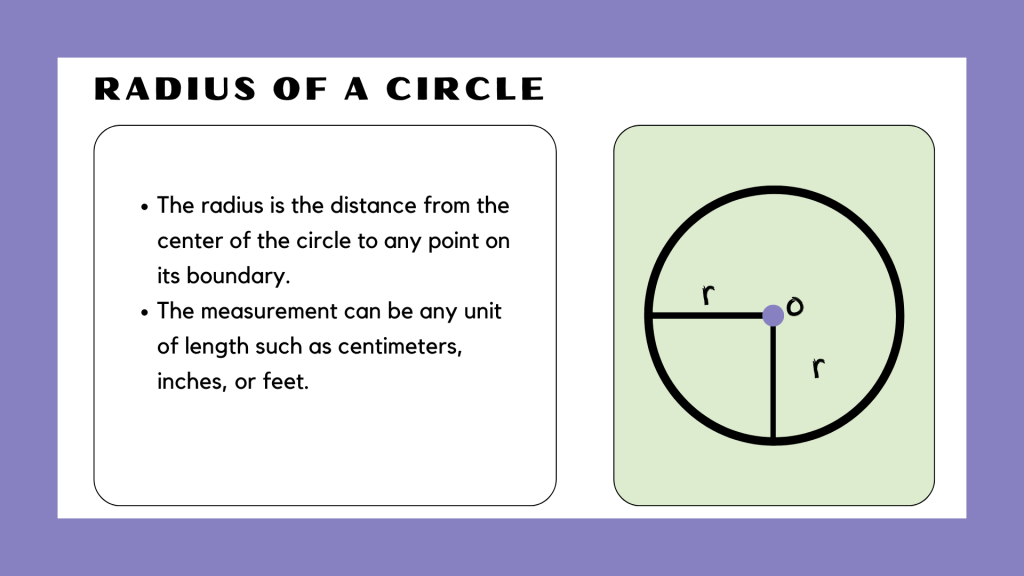
Radius
The radius is the distance from the center of the circle to any point on its circumference. It is a constant length for a given circle and is denoted by the letter “r”. The radius is crucial in defining the size of the circle and in various calculations involving the circle.
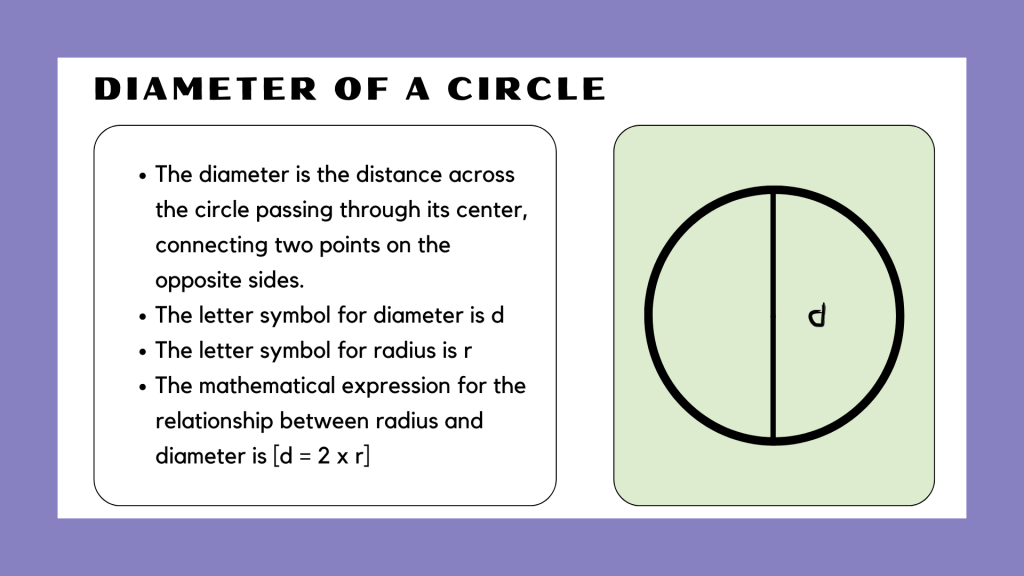
Diameter
The diameter of a circle is the longest distance across the circle, passing through the center. It is twice the length of the radius, thus 𝑑 = 2𝑟. The diameter is an important measure because it represents the width of the circle and is often used in formulas involving the circle’s circumference and area.
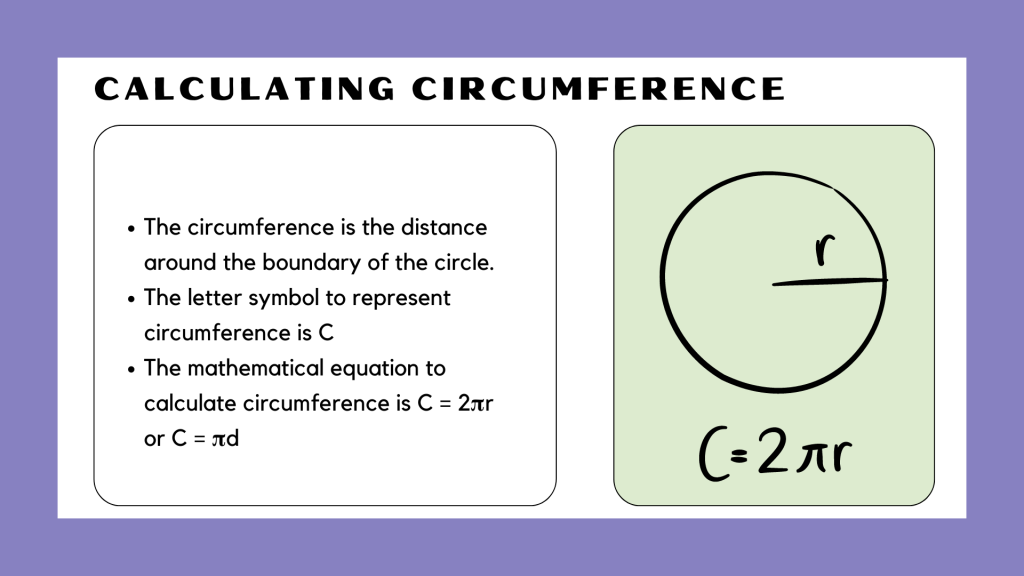
Method
Calculating Circumference
To calculate the circumference of a circle, the formula C = 2πr can be utilized, where r is the radius of the circle. Alternatively, the formula C = πd, where d represents the diameter, can also be employed to determine the circumference.
Examples
Example 1: Given the radius of a circle as 5 units, calculate the circumference.
Using the formula C = 2πr, where r = 5, the circumference is C = 2 x 3.14159 x 5 = 31.4159 units.
Example 2: If the diameter of a circle is 12 units, determine the circumference using the formula C = πd.
Substituting d = 12 into the formula, the circumference is C = 3.14159 x 12 = 37.6991 units.
Example 3: Calculate the circumference of a circle with a radius of 8 units using the formula C = 2πr.
By substituting r = 8 into the formula, the circumference is C = 2 x 3.14159 x 8 = 50.2655 units.
Summary::
These examples illustrate the application of the circumference formula in calculating the distance around circular shapes. By substituting the given values of radius or diameter into the respective formulas, the circumference of the circle can be accurately determined, showcasing the practical utility of the formula in solving mathematical problems.
These examples illustrate the application of the circumference formula in calculating the distance around circular shapes. By substituting the given values of radius or diameter into the respective formulas, the circumference of the circle can be accurately determined, showcasing the practical utility of the formula in solving mathematical problems.
Quiz
Tips and Tricks
1. Using the Radius
Tip: Utilize the formula C = 2πr to calculate the circumference by substituting the given radius into the formula.
2. The Diameter Dilemma
Tip: Use the formula C = πd to calculate the circumference by substituting the given diameter into the formula.
3. Check Units
Always make sure your units are consistent. If the radius is in centimeters, the circumference will be in centimeters. Mixing units can lead to incorrect calculations.
4. Visualize with Real-World Objects
To better understand circumference, visualize or measure the circumference of circular objects like: A plate (using a string around the edge and then measuring the string). or A wheel or tire (rolling it to see how far it travels in one complete rotation).
Real life application
Story: The Circumference Quest of Sarah and David
Sarah and David, two enthusiastic explorers, embarked on a quest filled with challenges that required the application of the circumference formula to overcome obstacles and achieve success.
Challenge 1: The Circular Garden
Sarah and David encountered a circular garden and needed to determine the length of the fence required to enclose it. By applying the formula C = 2πr, where r represents the radius of the garden, they accurately calculated the circumference and obtained the necessary length of fencing.
Challenge 2: The Ferris Wheel Dilemma
Continuing their quest, Sarah and David encountered a massive Ferris wheel and were tasked with calculating the distance traveled by a passenger in one complete revolution. By utilizing the formula C = πd, where d represents the diameter of the wheel, they successfully determined the circumference and solved the dilemma.
Challenge 3: The Circular Pipeline Predicament
In their final challenge, Sarah and David were presented with a circular pipeline project that required accurate measurements. By employing the circumference formula, they calculated the length of the pipeline and ensured the successful completion of the project.
FAQ's
The formula for finding the circumference of a circle is C = 2πr, where C represents the circumference, π is a constant approximately equal to 3.14159, and r is the radius of the circle.
Understanding the formula for finding the circumference of a circle is crucial as it allows for accurate calculations in various mathematical and real-life scenarios, such as geometry, engineering, and construction.
Yes, the circumference of a circle can also be calculated using the formula C = πd, where d represents the diameter of the circle. This provides an alternative method for determining the circumference.
The circumference of a circle is directly proportional to its diameter, as the formula for finding the circumference can be expressed as C = πd, where d is twice the radius (d = 2r).
The concept of circumference finds practical applications in various real-life scenarios such as calculating the distance around circular objects, determining the length of curved structures, and designing circular components in engineering and architecture.
Like? Share it with your friends
Facebook
Twitter
LinkedIn