How to Find Surface Area? – Formulas & Examples
Table of Contents
Introduction
What is Surface Area?
In the field of geometry, surface area refers to the total area that the surface of a 3-D ( three dimensional) object occupies. It is an important concept in mathematics and is used to calculate the amount of material needed to cover or paint the surface of an object. There are two main types of surface area: lateral surface area and total surface area. Let’s explore the formulas and methods for calculating surface area for various geometric shapes.
Analogy of Definition
The Types of Surface Area
The two types of surface area are:
1. Lateral Surface Area: This refers to the area of the lateral (side) surface of a three-dimensional object, excluding the top and bottom surfaces.
2. Total Surface Area: This includes the area of all the surfaces of a three-dimensional object, including the lateral, top, and bottom surfaces.
Method
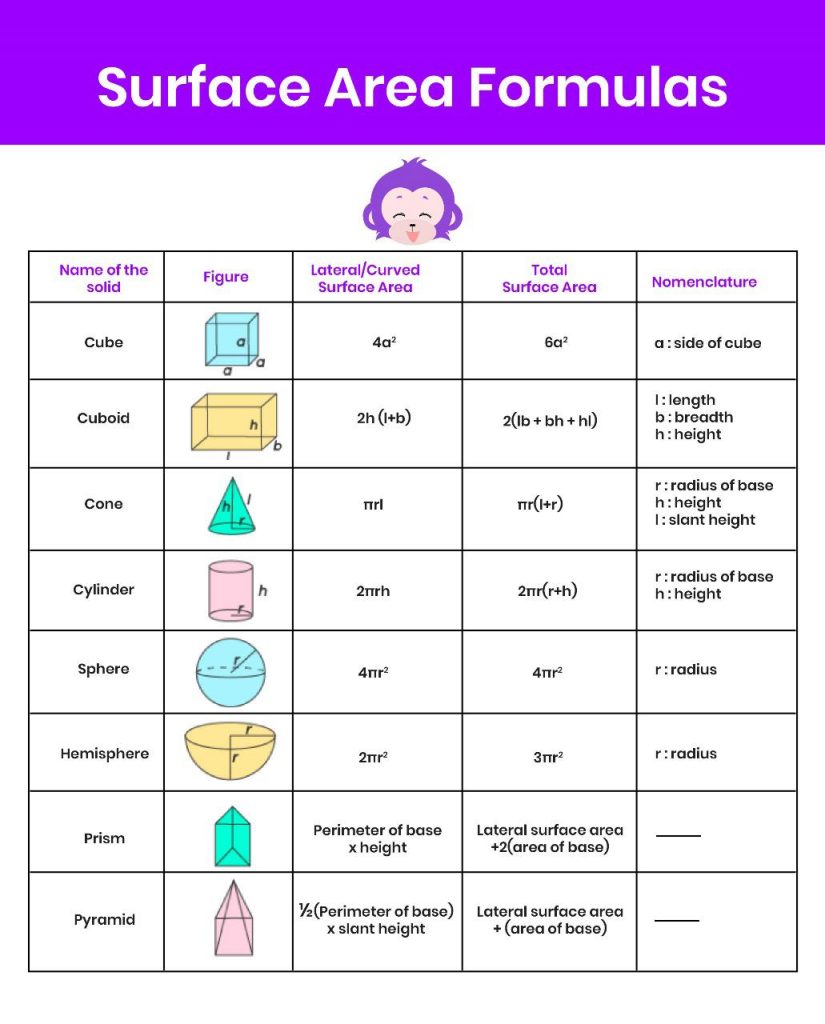
Formulas for Calculating Surface Area:
The formulas for calculating the lateral and total surface area of various geometric shapes are as follows:
1. Sphere
Lateral Surface Area = Not Applicable
Total Surface Area = 4πr2, where r is the radius of the sphere.
2. Cylinder
Lateral Surface Area = 2πrh
Total Surface Area = 2πr(r + h),
where,
r = radius of the cylinder,
h = height of the cylinder
3. Rectangular Prism:
Lateral Surface Area = 2(lw + lh + wh)
Total Surface Area = 2lw + 2lh + 2wh,
where,
l = length of the prism /cuboid
w = width of the prism / cuboid
h = height of the prism / cuboid
4. Cone:
Lateral Surface Area = πrl
Total Surface Area = πr(r + l),
where,
r = radius of the cone,
l = slant height of the cone
5. Cube:
Lateral Surface Area = 4a2
Total Surface Area = 6a2
where,
a = length of each side of the cube
6. Triangular Prism:
Lateral Surface Area = ph
where,
p = perimeter of the base
h = height of the prism
Total Surface Area = (Perimeter of the base × Length of the prism) + (2 × Base Area) = (a1 +a2 + a3)L + bh
where,
h is the height of the base triangle,
L is the length of the prism,
b is the bottom of the prism,
a1, a2, and a3 are the three edges (sides) of the base triangle
(bh) is the combined area of the two triangular faces [2 × (1/2 × bh)] = bh
7. Pyramid:
Lateral Surface Area = 1/2 * p * l
Total Surface Area = 1/2 * p * l + B,
where.
p = perimeter of the base,
l = length of the pyramid,
B = Base Area
Learn more about Areas in a fun and interactive way, on ChimpVine.
Examples
Example 1: Find the total surface area of a right triangular prism which has a base area of 20 square units, the base perimeter of 10 units, and the length of the prism is 5 units.
Solution: Given, base area = 20 square units, base perimeter = 10 units and length of prism = 5 units
The surface area of the right triangular prism is Surface Area = (Perimeter of the base × Length of the prism ) + (2 × Base Area)
SA = (10 × 5) + (2 × 10)
SA = (50 + 20) square units
SA = 70 square units
Hence, the surface area of the right triangular prism is 70 square units.
Example 2: Find out the surface area of a cube whose each side measures 5 inches.
Solution: Given side length of cube (a) = 3 inches.
The surface area of a cube = 6a2
SA = 6a2
SA = 6 * 52
SA = 150 inches2
∴ The surface area of the cube is 150 inches2.
Example 3: If the radius and slant height of a is 6 inches and 3 inches respectively. Find its surface area.
Solution:
Given: radius (r) = 6 inches and slant height (l) = 3 inches.
Surface area of cone = πr(r + l)
SA = π × 6 inch × (6 + 3) inch
SA = 3.14 × 6 inches × 9 inches
SA = 169.56 inches2
Hence, The surface area of the cone is 169.56 inches2.
Quiz
Tips and Tricks
1. Calculating the Surface Area of a Sphere
Tip: Use the formula Total Surface Area = 4πr2 to find the total surface area of a sphere.
2. Finding the Lateral Surface Area of a Cylinder
Tip: Use the formula Lateral Surface Area = 2πrh to calculate the lateral surface area of a cylinder.
3. Calculating the Total Surface Area of a Rectangular Prism
Tip: Use the formula Total Surface Area = 2lw + 2lh + 2wh to find the total surface area of a rectangular prism.
4. Determining the Lateral Surface Area of a Cone
Tip: Use the formula Lateral Surface Area = πrl to calculate the lateral surface area of a cone.
5. Finding the Total Surface Area of a Cube
Tip: Use the formula Total Surface Area = 6a2 to determine the total surface area of a cube.
Real life application
Story: “The Surface Area Adventures of Maya and Ethan”
Maya and Ethan, two young explorers, encountered real-life situations where the concept of surface area played a crucial role in solving problems and completing tasks.
Challenge 1: The Paint Project
Maya and Ethan volunteered to paint the walls of a community center. They needed to calculate the total surface area of the walls to determine the amount of paint required. By using the formula for the total surface area of a rectangular prism, they were able to estimate the quantity of paint needed and successfully completed the project.
Challenge 2: The Garden Makeover
In another adventure, Maya and Ethan helped redesign a garden by installing a new fountain. They needed to calculate the lateral surface area of the fountain to determine the amount of decorative tiles required to cover it. Using the formula for the lateral surface area of a cone, they were able to make accurate measurements and complete the installation with precision.
Challenge 3: The Packaging Puzzle
Maya and Ethan were tasked with packaging gift boxes for a charity event. They needed to calculate the total surface area of the boxes to determine the amount of wrapping paper needed. By applying the formula for the total surface area of a cube, they efficiently wrapped the boxes and contributed to the success of the event.
FAQ's
Calculating the surface area of geometric shapes is important in various real-life scenarios, such as construction, architecture, packaging, and design. It helps in determining the amount of material needed to cover or paint the surface of an object, making it a valuable tool in planning and executing projects.
The lateral surface area refers to the area of the lateral (side) surface of a three-dimensional object, while the total surface area includes the area of all the surfaces of the object, including the lateral, top, and bottom surfaces.
Yes, the concept of surface area has practical applications in real-life situations, such as painting walls, packaging boxes, designing structures, and calculating material requirements for construction and renovation projects.
Yes, there are specific formulas for calculating the lateral and total surface area of geometric shapes, including spheres, cylinders, rectangular prisms, cones, cubes, triangular prisms, and pyramids. These formulas are essential for accurately determining the surface area of various objects.
The concept of surface area provides a systematic approach to problem-solving and decision-making in real-life scenarios. It helps in making accurate measurements, estimating material requirements, and optimizing resource allocation, making it an essential tool for efficient planning and execution of tasks and projects.
Like? Share it with your friends
Facebook
Twitter
LinkedIn