How to Find the Area of Polygons? – Formula and Examples
Table of Contents
Introduction
Area of Polygon
In the realm of geometry, the concept of area plays a crucial role in determining the space occupied by two-dimensional shapes. When it comes to polygons, understanding the area is essential for various mathematical and real-world applications. Let’s dive into the world of polygonal areas and explore the formulas and methods used to find the area of polygon.
Analogy of Definition
The area of a polygon refers to the measure of the space enclosed within the boundaries of the polygon. It is a quantitative representation of the surface covered by the polygon on a flat plane. The area of a polygon can be calculated using specific formulas based on the type of polygon, whether it is regular or irregular.
Method
Calculating the Area of Polygon
The methods for calculating the area of a polygon vary depending on the type of polygon. For regular polygons, there are specific formulas that directly yield the area based on the side length and apothem (distance from the center to the midpoint of any side). In the case of irregular polygons, the area can be determined by dividing the polygon into smaller, more definite shapes and summing up their individual areas.
Calculating the Area of Polygon – Regular Polygons
The area of a regular polygon can be calculated using the formula: Area = 1/2 * Perimeter * Apothem. This formula takes into account the perimeter (the total length of all sides) and the apothem of the regular polygon. The apothem is a crucial component in determining the area of a regular polygon, as it represents the distance from the center to the midpoint of any side. The formula for calculating the apothem is \frac{I}{2tan(\frac{180}{n})}, where I stands for side lengths, and n is the number of sides.
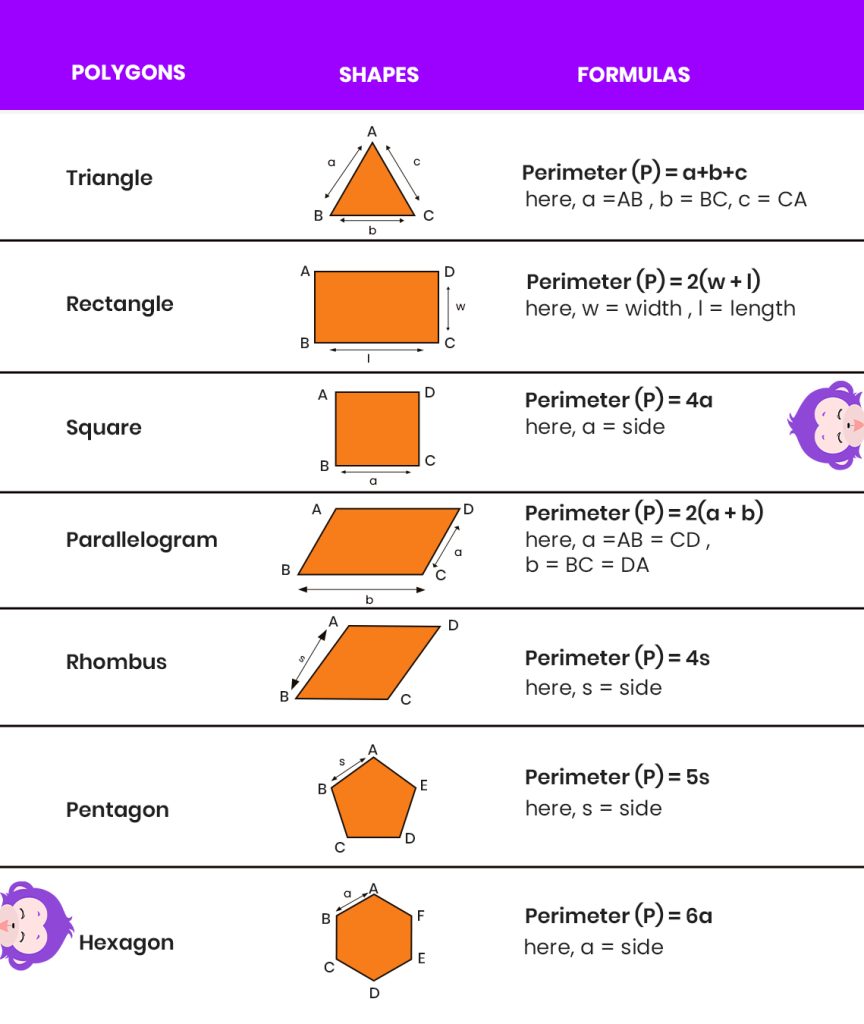
However, for the commonly known polygons, there are specific formulas and the variance in the formula is brought by the difference in types of polygon. The formula for the area of polyons are listed below.
Calculating the Area of Polygon – Irreggular Polyogns
The area of an irregular polygon can be determined by dividing it into smaller, simpler shapes such as triangles, rectangles, or trapezoids. Once the irregular polygon is decomposed into these basic shapes, the area of each individual shape can be calculated using the respective area formulas. The total area of the irregular polygon is then obtained by summing up the areas of the smaller shapes.
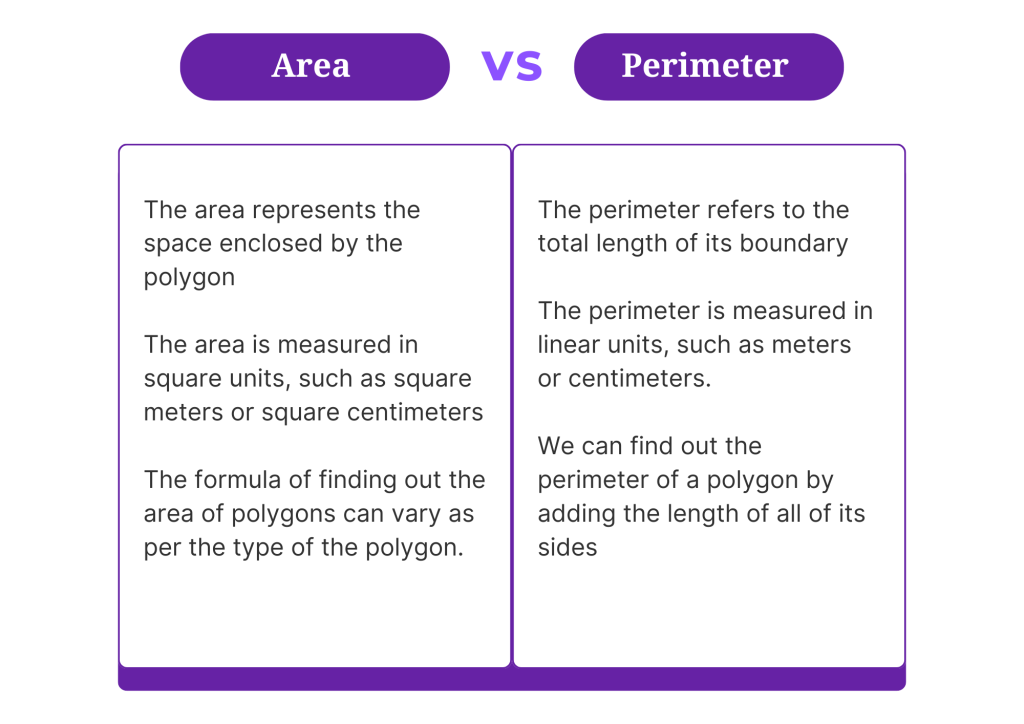
Difference betweem Perimeter and Area of Polygon
Area of Polygon
Examples
Example 1: Finding the Area of a Regular Hexagon
Step 1: Determine the side length and apothem of the regular hexagon
Side length = 6 cm
Apothem = 5.2 cm
Step 2: Use the area formula for regular polygons
Area = 1/2 * Perimeter * Apothem
Area = 1/2 * (6 cm * 6) * 5.2 cm
Area = 1/2 * 36 cm * 5.2 cm
Area = 18 cm * 5.2 cm
Area = 93.6 cm²
So, the area of the regular hexagon is 93.6 square centimeters.
Example 2: Finding the Area of Irregular Polygons
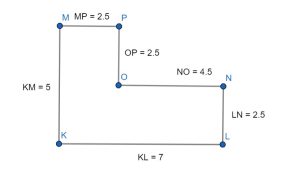
To solve the figure, first we will have to divide the shapes into proper polygons.
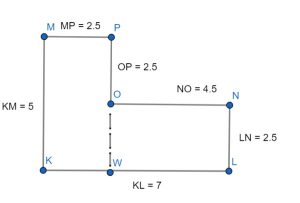
We have divided the figure into two rectangles, now we will find out the areas of the rectangle and add them.
Area of the polygon = Area of KMPW + Area of LNOW = 12.5 cm2 + 11.25 cm2 = 23.75cm2
Quiz
Tips and Tricks
1. Area of Irregular Polygons
Tip: You can find out the area of polygons by decomposing it into different regular polygon shapes.
2. Units of Measurement
Tip: While finding out the area, it is important that we pay attention the unit of measurement we are using to calculate.
3. Area of Heptagon
Tip: Use the area formula for regular polygons, considering the side length and apothem of the heptagon.
Area = 1/2 * Perimeter * Apothem
4. Regular and Irregular Polygons
Tips: If a polygon has sides or angles different in measure, then the polygon is known to be irregular.
Real life application
Story: “The Area Adventures of Maya and Ethan”
Maya and Ethan, two young explorers, embarked on a series of adventures that required them to apply their knowledge of area of polygons to overcome challenges and solve real-world problems.
Challenge 1: The Garden Makeover
Maya and Ethan volunteered to help redesign a community garden with area of polygons. They calculated the area of the garden beds, which were shaped as regular hexagons and octagons, to determine the amount of soil and mulch needed for the makeover. By applying the area formulas for regular polygons, they efficiently planned the garden layout and resources.
Challenge 2: The Architectural Blueprint
As part of a school project, Maya and Ethan were tasked with creating a blueprint for a new building. They calculated the areas of the rooms, corridors, and outdoor spaces, which involved irregular polygonal shapes. By decomposing the irregular polygons into simpler shapes and summing up their areas, they accurately determined the total area of the building layout.
Challenge 3: The Land Surveying Quest
In their final challenge, Maya and Ethan joined a land surveying team to measure and map out a piece of land with irregular boundaries. They utilized their knowledge of calculating the area of irregular polygons to accurately assess the land area for development and conservation purposes. Their expertise in polygonal areas contributed to the successful completion of the land surveying quest.
FAQ's
Understanding the area of a polygon is essential in various fields such as architecture, engineering, urban planning, and design. It enables accurate measurement and allocation of space, resources, and materials in real-world applications. Additionally, the area of a polygon serves as a fundamental concept in geometry and mathematical problem-solving.
The area of a regular polygon can be directly calculated using specific formulas based on the side length and apothem, while the area of an irregular polygon requires decomposition into smaller shapes and summation of their individual areas. Regular polygons have symmetrical and uniform properties, making their area calculations more straightforward, whereas irregular polygons have varying side lengths and angles, requiring a more intricate approach to determine their area.
The area of a polygon represents the space enclosed by its boundaries and is measured in square units, while the perimeter of a polygon refers to the total length of its boundary and is measured in linear units. The area provides information about the surface covered by the polygon, while the perimeter indicates the distance around the polygon.
Yes, the area of a polygon is commonly used to determine the quantity of materials required for projects such as landscaping, construction, flooring, and painting. By accurately calculating the area of the polygonal space to be covered, the amount of soil, concrete, tiles, or paint needed can be determined, facilitating efficient resource allocation and planning.
The concept of area of polygon has practical applications in various real-life scenarios, including urban planning, architecture, interior design, landscaping, land surveying, and construction. It is used to calculate the space requirements, material quantities, and resource distribution for a wide range of projects, contributing to effective planning and execution.
Like? Share it with your friends
Facebook
Twitter
LinkedIn