How to Find Volume? – Formula and Examples
Table of Contents
Introduction
Volume
In geometry, the concept of volume plays a crucial role in determining the amount of space occupied by a three-dimensional object. Whether it’s a simple cube or a complex cylinder, understanding how to find the volume of various shapes is essential for solving mathematical problems and real-world applications.
Analogy of Definition
What is Volume?
Volume refers to the amount of space occupied by a three-dimensional object. It is measured in cubic units, such as cubic centimetres or cubic meters. The volume of an object can be calculated by determining the total amount of space it encloses.
Method
How to Find Volume?
The method for finding the volume of different shapes varies based on their unique properties. For example, the volume of a cube can be found by simply cubing the length of one of its sides, while the volume of a cylinder requires the use of its base area and height. Understanding the specific formulas and techniques for each shape is essential for accurate volume calculations.
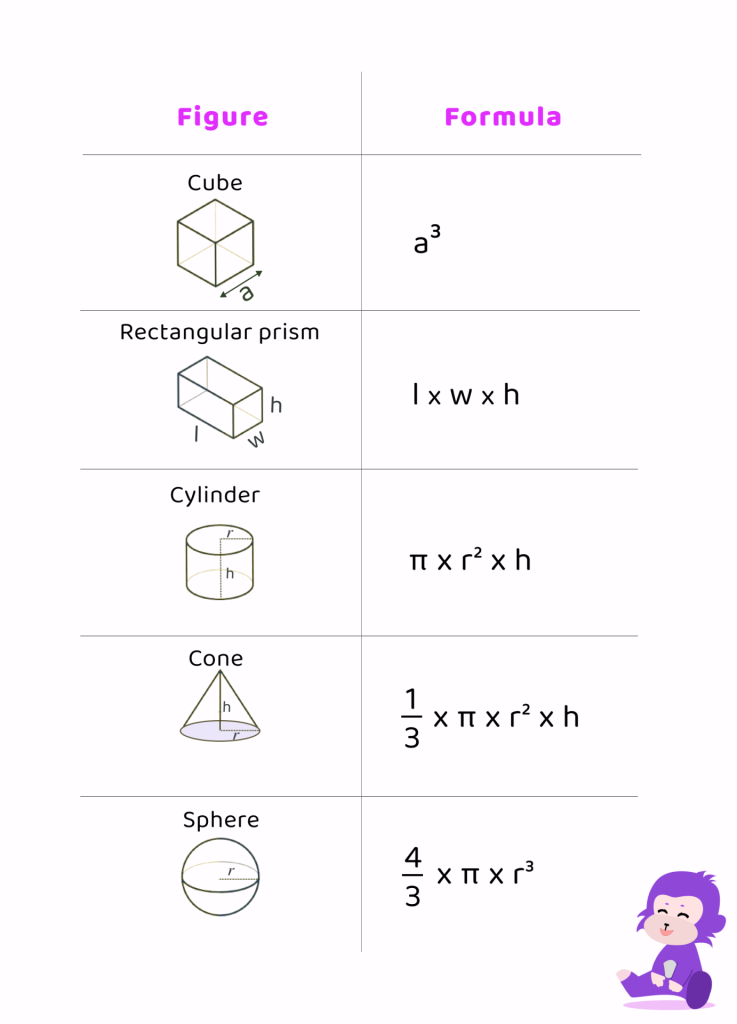
Volume of 3 Dimensional Shapes
Volume of a Cylinder
The volume (V) of a cylinder can be calculated using the formula:
V = πr2h
Where,
V = Volume
π = Pi (approximately 3.14159)
r = Radius of the base
h = Height of the cylinder
Volume of a Rectangular Prism / Cuboid
The volume (V) of a rectangular prism can be calculated using the formula:
V = l * w * h
Where,
V = Volume
l = Length
w = Width
h = Height
Volume of Sphere
The volume (V) of a sphere can be calculated using the formula:
V = (4/3)πr3
Where:
V = Volume
π = Pi (approximately 3.14159)
r = Radius of the sphere
Volume of Cube
The volume (V) of a cube can be calculated using the formula:
V = s 3
Where:
V = Volume
s = Length of one side of the cube
Volume of Cone
The volume (V) of a cone can be calculated using the formula:
V = (1/3)πr2h
Where:
V = Volume
π = Pi (approximately 3.14159)
r = Radius of the base
h = Height of the cone
Volume Formulas
Learn about volume in a fun and interactive way, visit our site ChimpVine.
Examples
Finding the Volume of Different Shapes
Example 1: Finding the Volume of a Cylinder
Given: Radius (r) = 5 cm, Height (h) = 10 cm
Using the formula V = πr2h
V = π * (5cm)2 * 10 cm
V ≈ 785.4 cm3
Example 2: Finding the Volume of a Rectangular Prism
Given: Length (l) = 6 cm, Width (w) = 4 cm, Height (h) = 3 cm
Using the formula V = l * w * h
V = (6 x 4 x 3) cm
V = 72 cm3
Example 3: Finding the Volume of a Sphere
Given: Radius (r) = 3 cm
Using the formula V = (4/3)πr3
V = (4/3) * π * (3 cm)3
V ≈113.1 cm3
Example 4: Finding the Volume of a Cube
Given: Length of side (s) = 5 cm
Using the formula V = s3
V = (5 cm)3
V = 125 cm3
Example 5: Finding the Volume of a Cone
Given: Radius (r) = 4 cm, Height (h) = 8 cm
Using the formula V = (1/3)πr2h
V = (1/3) * π * (4 cm)2 * (8 cm)
V ≈ 134.04 cm 3
Quiz
Tips and Tricks
1. The Cylinder Challenge
Tip: Use the formula V = πr2h to calculate the volume of a cylinder. If the radius and height of a cone is equal, then its volume will be 1/3 th the volume of cylinder.
2. The Rectangular Prism Puzzle
Tip: Use the formula V = l * w * h to find the volume of a rectangular prism. Rectangular prism is also known to be a cuboid.
3. The Sphere Quest
Tip: Use the formula V = (4/3)πr3 to calculate the volume of a sphere.
4. The Cube Conundrum
Tip: Use the formula V = s3 to determine the volume of a cube.
5. The Cone Challenge
Tip: Use the formula V = (1/3)πr2h to find the volume of a cone.
Real life application
Story: “The Volume Adventures of Maya and Ethan”
Maya and Ethan, two young explorers, embarked on a series of adventures that required them to apply their knowledge of volume to overcome challenges and solve mysteries.
Challenge 1: The Treasure Chamber
Maya and Ethan discovered an ancient treasure chamber filled with various geometric artifacts. To unlock the chamber, they needed to calculate the volume of a cylindrical container that held precious gems. Using the formula V = πr2h they determined the volume and gained access to the treasure.
Challenge 2: The Enchanted Forest
As they ventured into an enchanted forest, Maya and Ethan encountered a magical sphere that emitted a mysterious glow. To understand its significance, they calculated the volume of the sphere using the formula V = (4/3)πr3. The volume revealed the sphere’s hidden power, guiding them on their quest.
Challenge 3: The Secret Temple
In their final challenge, Maya and Ethan entered a secret temple where they encountered a massive rectangular prism that concealed a legendary artifact. By calculating the volume of the prism using the formula V = lwh, they unveiled the artifact and completed their extraordinary journey.
FAQ's
Finding the volume of different shapes is essential for determining the amount of space they occupy, which is crucial in various real-world applications such as architecture, engineering, and construction. It also plays a key role in solving mathematical problems related to geometry and spatial reasoning.
The formula for finding the volume of a cylinder involves the use of its base area (πr2) and height (h), while other shapes have unique formulas based on their specific dimensions and properties. Understanding the distinct formulas for each shape is essential for accurate volume calculations.
Yes, the concept of volume can be extended to irregular shapes by using methods such as integration in calculus or the use of displacement in fluid mechanics. While the formulas for regular shapes are straightforward, calculating the volume of irregular shapes may require advanced mathematical techniques.
The volume of a cube is directly related to its surface area, as both measurements are essential for understanding the spatial characteristics of the cube. While the volume represents the space enclosed by the cube, the surface area reflects the total area of its external faces.
Real-life examples of volume calculations include determining the capacity of containers, calculating the amount of material needed for construction projects, and understanding the displacement of fluids in engineering applications. Volume calculations are also used in fields such as manufacturing, transportation, and environmental science.
Like? Share it with your friends
Facebook
Twitter
LinkedIn
