Understanding Integers: Definition and Properties

Introduction

Integers

In the realm of mathematics, the concept of integers plays a fundamental role in representing whole numbers and their properties. Let’s delve into the world of integers and explore their definition and properties.

Analogy of Definition

What are Integers?

Integers encompass all whole numbers, including positive and negative numbers, as well as zero. They are essential in various mathematical operations and provide a comprehensive representation of numerical values.

Positive Integers (+1, +2, +3, …): Positive integers are whole numbers greater than zero. They are used to represent quantities that are counted or measured in a positive direction.

Negative Integers (-1, -2, -3, …): Negative integers are whole numbers less than zero. They are used to represent quantities that are counted or measured in a negative direction, or to indicate a deficit or decrease.

Zero (0): Zero is a special integer that represents the absence of quantity or the neutral point between positive and negative numbers. It serves as the origin on the number line.

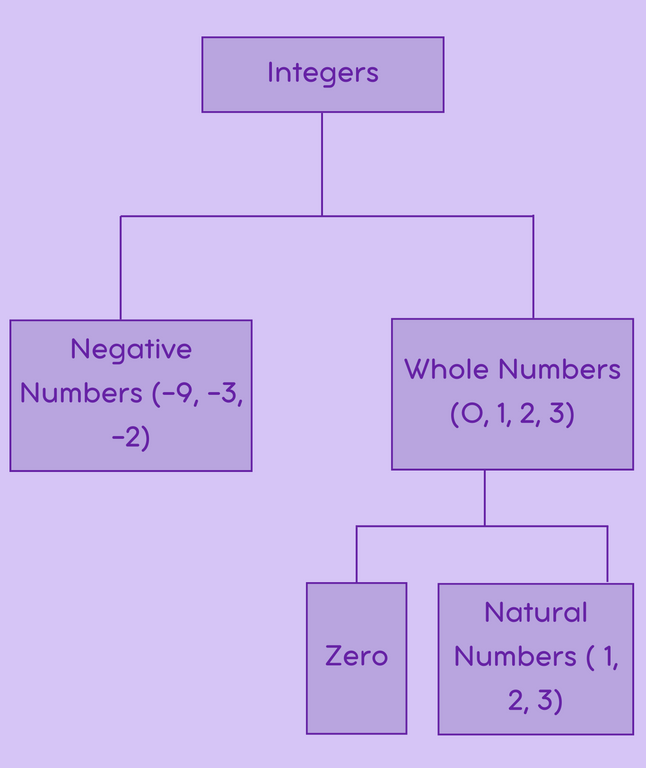
Types of Integers

1. Natural Numbers (N): Natural numbers are the set of positive integers starting from 1 and going infinitely (1, 2, 3, …). They are used for counting and representing quantities of objects.

2. Whole Numbers (W): Whole numbers include all the natural numbers along with zero (0, 1, 2, 3, …). They are used for counting, measuring, and describing situations where zero is relevant.

3. Negative Integers (-N): Negative integers are the set of integers less than zero (-1, -2, -3, …). They are used to represent deficits, losses, or quantities measured in a negative direction.

Integers on a Number Line

Integers can also be represented visually with the help of a number line. In the following representation, we’ll illustrate how integers are depicted on a number line, providing a visual aid to comprehend their order and relationships.

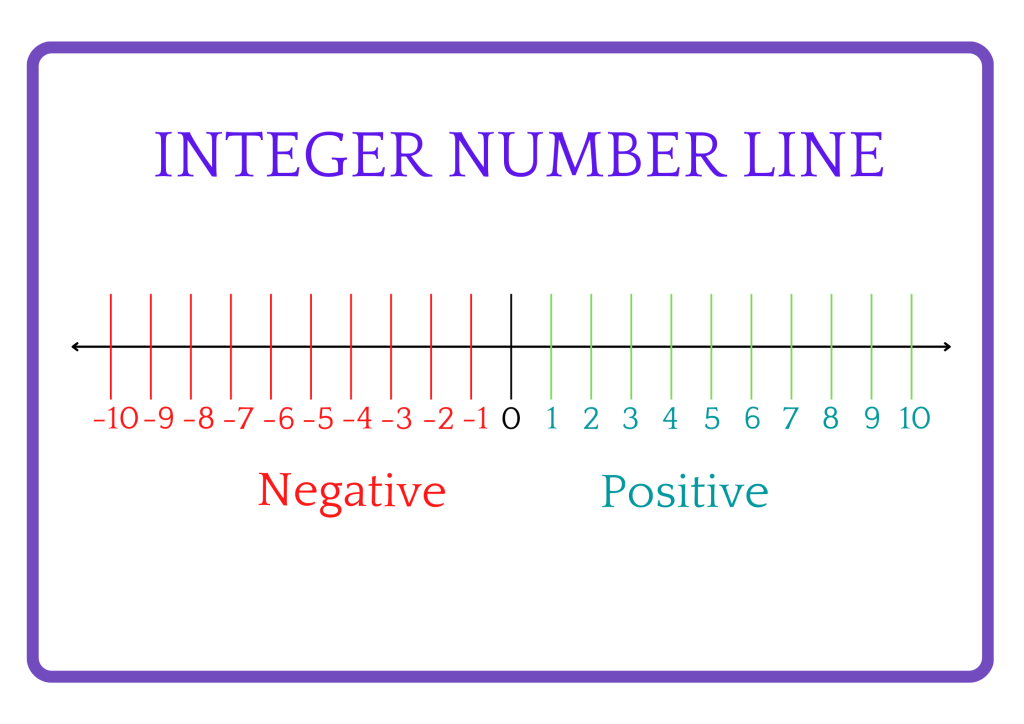
Here’s how integers are represented on a number line:

The number line is a horizontal line extending infinitely in both directions.
The integers are marked as equally spaced points on the number line.
Zero (0) is at the center of the number line, acting as the reference point or origin.
To the left of zero are the negative integers, such as -1, -2, -3, and so on, represented by points to the left of zero.
To the right of zero are the positive integers, such as 1, 2, 3, and so on, represented by points to the right of zero.

Each point on the number line corresponds to an integer, with the distance between consecutive integers being the same. This visual representation helps understand the relative positions and magnitudes of integers.

Method

Properties of Integers

Integers exhibit several key properties, including closure under addition and subtraction, the existence of an additive identity (zero), and the presence of additive inverses for every integer.

1. Closure Property: Integers are closed under addition and subtraction. This means that when you add or subtract two integers, the result is always an integer.

2. Commutative Property: Addition and subtraction of integers are commutative. This means that changing the order of the numbers being added or subtracted does not change the result. For example, a + b = b + a and a – b = b – a for any integers a and b.

3. Associative Property: Addition and subtraction of integers are associative. This means that when adding or subtracting three or more numbers, the grouping of the numbers does not affect the result. For example, (a + b) + c = a + (b + c) and (a – b) – c = a – (b – c) for any integers a, b, and c.

4. Identity Elements: Zero (0) serves as the additive identity for integers. This means that adding zero to any integer leaves it unchanged (a + 0 = a for any integer a). Each integer also has an additive inverse, which is the negative of the integer. Adding an integer to its additive inverse results in zero (a + (-a) = 0 for any integer a).

5. Distributive Property: Multiplication distributes over addition and subtraction for integers. This means that a number multiplied by the sum or difference of two other numbers is equal to the sum or difference of the products of the number multiplied by each of the other two numbers individually. For example, a × (b + c) = a × b + a × c and a × (b – c) = a × b – a × c for any integers a, b, and c.

Integers Operations

Addition

Integers can be added together using the addition operation (+). When adding two positive integers, the result is positive. When adding two negative integers, the result is negative.
When adding a positive integer and a negative integer, the result depends on the magnitude of the numbers: If the positive integer has a greater magnitude, the result is positive. If the negative integer has a greater magnitude, the result is negative. If the magnitudes are equal, the result is zero.

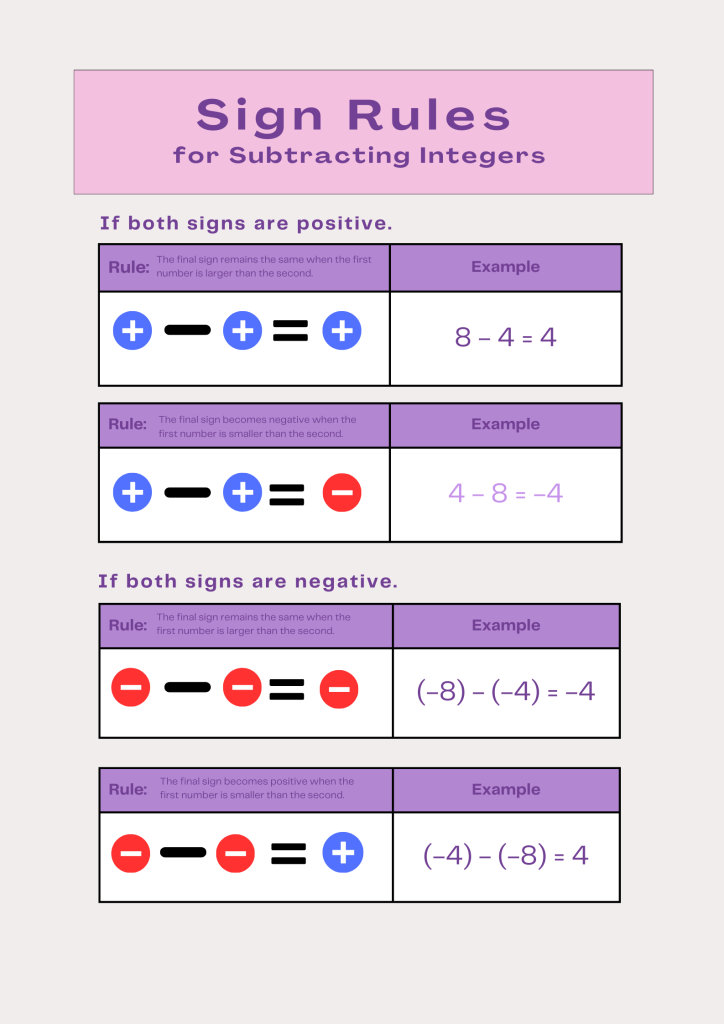
Subtraction

In the context of integers, subtraction follows a specific rule to determine the result. When subtracting one integer from another, it is equivalent to adding the additive inverse of the subtrahend. For example, when subtracting 3 from 5 (5 – 3), we can interpret it as adding the additive inverse of 3 to 5. The additive inverse of 3 is -3. Therefore, 5 – 3 is equivalent to 5 + (-3). Adding a negative integer is the same as subtracting its positive counterpart. So, in this case, we’re effectively subtracting 3 from 5, resulting in 2.

Multiplying Integers

Integers can be multiplied together using the multiplication operation (×). When multiplying two integers with the same sign (both positive or both negative), the result is positive.
When multiplying two integers with different signs (one positive and one negative), the result is negative.

Example: (-4) × 3 = -12

Dividing Integers

Integers can be divided using the division operation (÷). Division by zero is undefined in integer arithmetic. Division of two integers may result in a quotient and a remainder.
Example: 10 ÷ (-2) = -5

Examples

Example 1: Adding 5 and -3 results in 2, demonstrating closure under addition.

Example 2: Subtracting 7 from 4 yields -3, showcasing closure under subtraction.

Example 3: The sum of any integer and its additive inverse is always zero, exemplifying the existence of additive inverses.

Example 4: Multiplying -6 by 2 results in -12, illustrating closure under multiplication.

Example 5: Dividing 15 by -3 yields -5, demonstrating closure under division.

Example 6: Adding -8 and -4 gives -12, showcasing the addition of negative integers.

Example 7: Subtracting -9 from -2 results in 7, highlighting the subtraction of negative integers.

Example 8: Multiplying -3 by -4 yields 12, illustrating the multiplication of negative integers.

Example 9: Dividing -20 by 5 gives -4, demonstrating the division of negative integers.

Example 10: Adding -10 and 10 results in 0, exemplifying the existence of additive inverses.

Example 11: Subtracting 0 from any integer leaves the integer unchanged, showcasing the identity property of subtraction.

Example 12: Multiplying any integer by 1 results in the same integer, illustrating the identity property of multiplication.

Summary:
The examples illustrate the fundamental properties of integers, including closure under addition and subtraction, as well as the existence of additive inverses. These properties form the basis for understanding the behavior of integers in mathematical operations and calculations.

Quiz

Tips and Tricks

1. Closure under Addition:

Scenario: Adding 8 and -5.
Tip: Integers exhibit closure under addition, resulting in the sum of two integers being an integer.
Calculation: 8 + (-5) = 3

2. The Zero Identity

Scenario: Adding 0 to any integer.
Tip: Zero serves as the additive identity for integers, leaving the integer unchanged when added.
Calculation: 7 + 0 = 7

3. Additive Inverses

Scenario: Finding the additive inverse of -9.
Tip: Every integer has an additive inverse that, when added, yields zero.
Calculation: -9 + 9 = 0

Real life application

Scenario: Temperature Representation
Integers are utilized to represent temperatures, with positive integers denoting hot temperatures and negative integers indicating cold temperatures. For instance, a temperature of 10 degrees Celsius is represented as +10, while a temperature of -5 degrees Celsius is represented as -5.

Scenario: Financial Transactions
Integers are employed in financial transactions to represent gains and losses. Positive integers signify profits, while negative integers denote losses. For example, a profit of $500 is represented as +500, while a loss of $200 is represented as -200.

Scenario: Distance Measurement
Integers are used to measure distances, with positive integers representing distances traveled in one direction and negative integers indicating distances traveled in the opposite direction. For instance, a distance of 5 miles traveled east is represented as +5, while a distance of 3 miles traveled west is represented as -3.

FAQ's

What are integers?

Integers are whole numbers that can be positive, negative, or zero. They do not have any fractional or decimal parts.

What are the properties of integers?

The properties of integers include closure under addition and subtraction, the existence of an additive identity (zero), and the existence of additive inverses for every integer.

How are integers represented on a number line?

Integers are represented on a number line with positive integers to the right of zero and negative integers to the left of zero. Zero is the neutral point on the number line.

What are the different types of integers?

The different types of integers include positive integers, negative integers, and zero. Positive integers are greater than zero, negative integers are less than zero, and zero is neither positive nor negative.

How are integers used in real-life situations?

Integers are used in real-life situations to represent quantities such as temperature, money, and distances. They are also used in mathematical operations and calculations.

Like? Share it with your friends