Line of Symmetry – Definition and Types
Table of Contents
Introduction
Line of Symmetry
In the world of geometry, the concept of symmetry plays a crucial role in understanding the balance and proportion of shapes and figures. One key aspect of symmetry is the “Line of Symmetry,” which is a line that divides a figure into two identical halves. Let’s explore the different types of lines of symmetry and their significance in geometric figures.
Analogy of Definition
What is Line of Symmetry?
A line of symmetry is a line that divides a figure into two congruent parts, such that if one part is folded over the line, it perfectly aligns with the other part. In geometric terms, a figure is said to have a line of symmetry if it can be folded along the line and the two halves match exactly.
Method
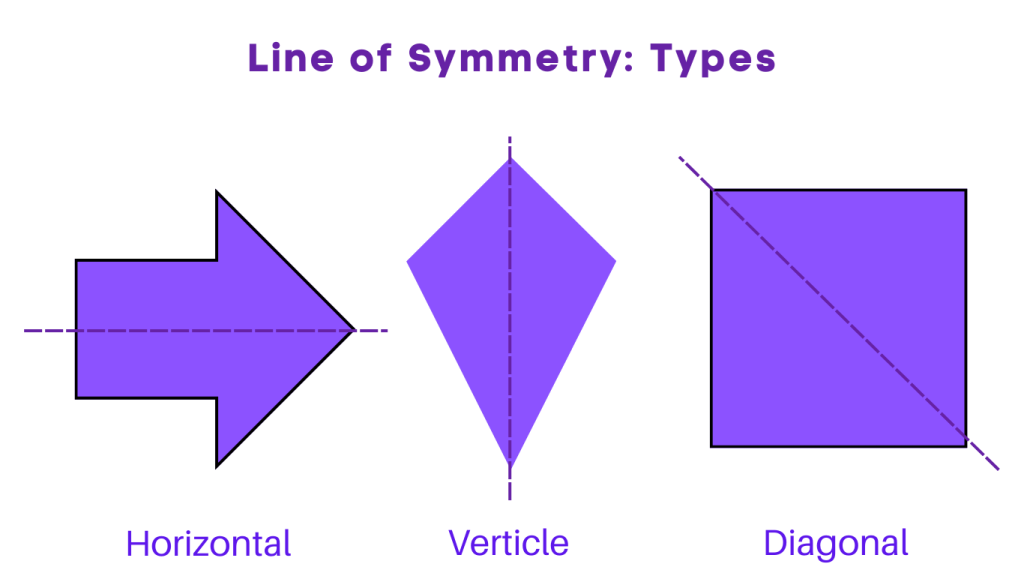
Types of Line of Symmetry
1. Horizontal Line of Symmetry
A horizontal line of symmetry is a line that runs horizontally through the center of a figure, dividing it into two mirror-image halves. Examples of figures with horizontal lines of symmetry include the square, rectangle, and the uppercase letters H, I, and T.
2. Vertical Line of Symmetry
A vertical line of symmetry is a line that runs vertically through the center of a figure, dividing it into two mirror-image halves. Examples of figures with vertical lines of symmetry include the circle, triangle, and the uppercase letters A, B, and C.
3. Diagonal Line of Symmetry
A diagonal line of symmetry is a line that runs diagonally through the center of a figure, dividing it into two mirror-image halves. Examples of figures with diagonal lines of symmetry include the rhombus, kite, and the uppercase letter X
Examples
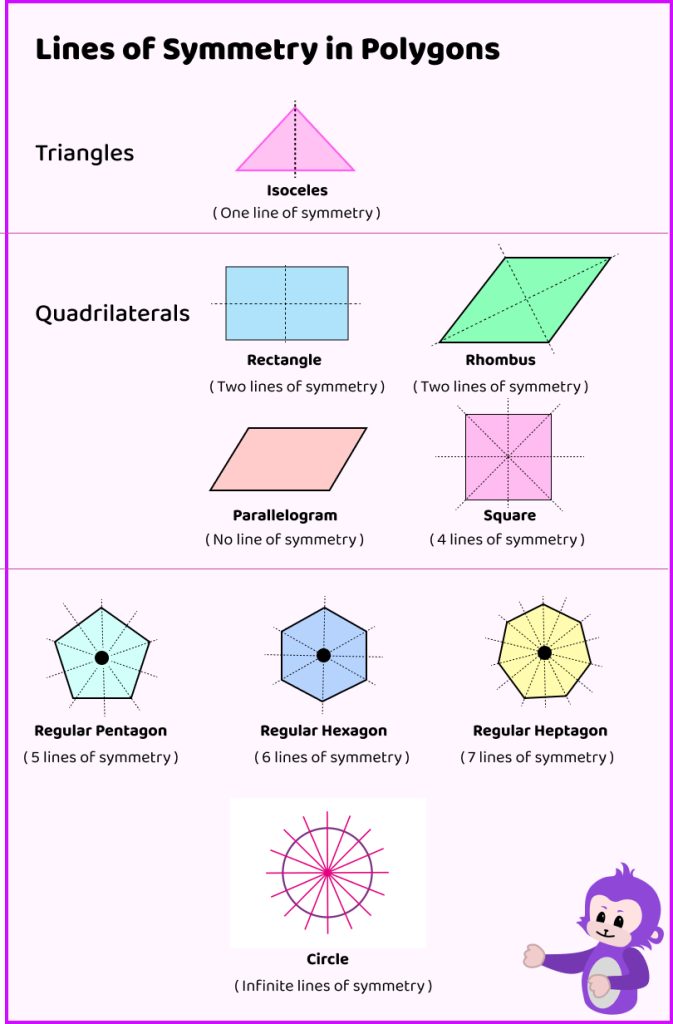
Number of Lines of Symmetry in Geometric Figures
1. Square
A square has 4 lines of symmetry – 2 horizontal and 2 vertical lines.
2. Rectangle
A rectangle is a polygon which has 2 lines of symmetry – 1 horizontal and 1 vertical line.
3. Circle
A circle has an infinite number of lines of symmetry, as any line passing through its center divides it into two equal halves.
4. Triangle
An equilateral triangle has 3 lines of symmetry – 3 medians, while an isosceles triangle has 1 line of symmetry – the line that bisects the base.
5. Rhombus
A rhombus has 2 lines of symmetry – 2 diagonals that bisect each other at right angles.
Quiz
Tips and Tricks
1.Identify Symmetrical Shapes
Tip: Look for shapes that have identical halves when folded along a line. Common symmetrical shapes include squares, rectangles, circles, and triangles (such as equilateral triangles).
2.Visualize Reflection
Tip: Imagine folding the shape along a line. If both halves match perfectly, then that line is the line of symmetry.
3.Check for Evenness
Tip:Symmetrical shapes have an equal number of points on each side of the line of symmetry. Count the points or vertices to verify symmetry.
4. Think About Nature
Tip:Nature is full of symmetrical patterns, such as butterfly wings, flower petals, and snowflakes. Observing natural symmetry can help reinforce the concept.
5. Use Symmetry in Art
Tip: Many artists use symmetry intentionally in their work. Study art pieces and notice how symmetry is used to create balance and harmony.
Real life application
Story: “The Line of Symmetry Quest of Maya and Ethan”
Maya and Ethan, two young explorers, embarked on a quest to uncover the secrets of symmetry in the world around them. As they journeyed through various landscapes, they encountered real-life examples of lines of symmetry in everyday objects.
Scenario 1: The Butterfly’s Wings
In a lush garden, Maya and Ethan marveled at the intricate patterns on a butterfly’s wings. They noticed that the wings had a line of symmetry running through the center, creating a mirror-image effect on both sides. This discovery inspired them to observe other symmetrical patterns in nature, such as flower petals and snowflakes.
Scenario 2: The Architect’s Blueprint
As they ventured into the city, Maya and Ethan visited a construction site where they observed the blueprint of a new building. They learned that architects and engineers use the concept of symmetry, including lines of symmetry, to design structures that are visually appealing and structurally sound. The blueprint revealed the use of vertical and horizontal lines of symmetry in the building’s design.
Scenario 3: The Kaleidoscope of Colors
In an art gallery, Maya and Ethan were captivated by a kaleidoscope that created mesmerizing symmetrical patterns. They realized that artists often incorporate lines of symmetry in their artwork to achieve balance and harmony. The kaleidoscope’s ever-changing designs showcased the beauty of symmetry in a creative and colorful way.
Scenario 4: The Reflection in the Lake
During a peaceful walk by the lake, Maya and Ethan noticed the reflection of trees and clouds on the water’s surface. They observed that the reflection created a mirror image, demonstrating the presence of a horizontal line of symmetry. This natural phenomenon highlighted the prevalence of symmetry in the environment.
Scenario 5: The Mirror’s Reflection
Back at home, Maya and Ethan experimented with a mirror and discovered that their own faces had a vertical line of symmetry. They had fun creating playful symmetrical poses and realized that symmetry is not only found in nature and art but also in everyday reflections.
FAQ's
Identifying the lines of symmetry in geometric figures helps in understanding the balance, proportion, and visual appeal of shapes. It is essential in art, architecture, and design, as well as in recognizing patterns in nature and everyday objects.
The number of lines of symmetry in geometric figures varies based on their shape and structure. Regular polygons such as squares and circles have multiple lines of symmetry, while irregular shapes may have fewer or no lines of symmetry.
Yes, lines of symmetry are commonly used in art and architecture to create visually appealing and harmonious designs. Artists and architects often incorporate symmetrical patterns and structures to evoke a sense of balance and beauty.
Yes, lines of symmetry are prevalent in nature and everyday objects. Examples include the symmetry of butterfly wings, flower petals, architectural designs, reflections in water, and artistic patterns, showcasing the widespread presence of symmetry in the world around us.
The concept of lines of symmetry can be applied in problem-solving by identifying balanced and symmetrical solutions. In creative endeavors, it can be used to create aesthetically pleasing designs, patterns, and structures that exhibit harmony and balance. By recognizing and leveraging lines of symmetry, one can achieve equilibrium and visual appeal, whether in artwork, architecture, or even in the arrangement of elements within a composition.
Like? Share it with your friends
Facebook
Twitter
LinkedIn