Understanding Lines and Their Properties in Geometry
Table of Contents
Introduction
Line Geometry
Lines are fundamental elements in the study of geometry, serving as the building blocks for understanding spatial relationships and shapes. Let’s delve into the realm of line geometry and explore its significance in the field of mathematics.
Analogy of Definition
Points
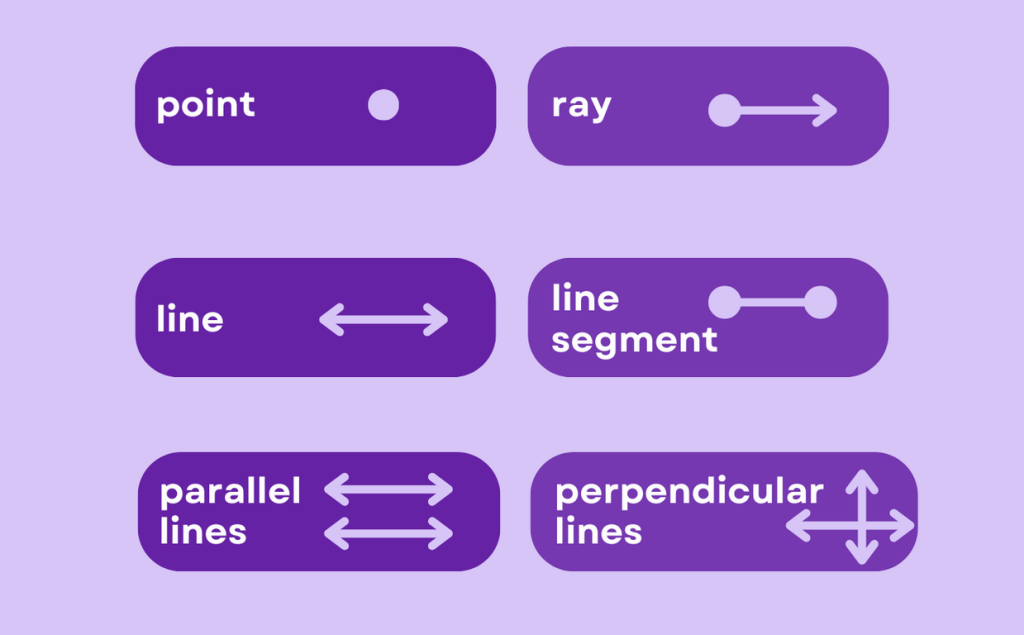
In geometry, a point is a fundamental object that represents a precise location in space. It has no length, width, or thickness and is often denoted by a dot. Points are considered to be dimensionless and are used as building blocks to define other geometric objects such as lines, planes, and shapes.
Properties of Points
- a position or location in space
Lines
In geometry, a line is a straight path that extends infinitely in both directions. It is one-dimensional and has no thickness or width. A line is composed of an infinite number of points. It is characterized by its length and direction, forming the basis for understanding the properties and relationships of geometric figures.
Properties of Lines
- never ends
- has two arrows
- goes forever in both directions
Ray
In geometry, a ray is a part of a line that consists of a single point (called the endpoint) and extends infinitely in one direction. Rays are one-dimensional geometric objects and can be thought of as “half-lines.” They have a starting point (the endpoint) and continue indefinitely in the specified direction.
Properties of Ray
- part of a line
- has 1 endpoint
- goes forever in one direction
Line Segment
A line segment is a part of a line that is bounded by two distinct endpoints. Unlike a line, which extends infinitely in both directions, a line segment has a finite length and is considered a one-dimensional object. A line segment is represented by a straight path connecting the two endpoints and does not continue beyond them.
Properties of Line Segment
- part of a line
- has 2 endpoints
Method
Types of Lines
The properties of lines in geometry encompass various types, including parallel lines, perpendicular lines, verticle line and horizontal line. Understanding these properties is essential for solving geometric problems.
Horizontal Lines
A horizontal line is a straight line that goes from left to right or right to left on a flat surface. It’s like the horizon you see when you look out at the sea or across a plain. Imagine drawing a line on a piece of paper without lifting your pencil, and that line goes perfectly straight from one side of the paper to the other, that’s a horizontal line. A horizontal line doesn’t go up or down at all, it just stretches straight across.
Vertical Line
A vertical line is a straight line that goes straight up and down, just like a tree trunk or a flagpole. It’s the opposite of a horizontal line, which goes left and right. If you imagine drawing a line on a piece of paper without moving your pencil to the left or right, but only up or down, that’s a vertical line.
Parallel Lines
Parallel lines are two or more straight lines that are always the same distance apart and never meet, no matter how far they are extended. They are like train tracks that run alongside each other but never intersect.
Perpendicular Lines
Perpendicular lines are two lines that intersect each other at a right angle or at 90°.
Examples
Quiz
Tips and Tricks
1. Rays
Tip: Remember that rays have one endpoint and extend infinitely in one direction. Think of rays as “starting from a point and going forever in a specific direction.”
2. Line Segments
Tip: Line segments have two distinct endpoints. Visualize them as a straight path with a clear beginning and end, like a section of a straight road.
3. Perpendicular Lines
Tip: Perpendicular lines intersect at a right angle, forming four 90-degree angles where they meet. Think of them as forming a square corner or “L” shape at their intersection.
4. Parallel Lines
Tip: Parallel lines never intersect and maintain a constant distance apart. Look for lines that appear to run side by side without converging or diverging.
5. Visualize and Compare
Tip: Draw diagrams or sketches to visualize the lines and their relationships. Use geometric shapes and angles to help identify perpendicular and parallel lines.
Real life application
Scenario: Architectural Design
Architects utilize the principles of line geometry to design structures, determine angles, and create spatial configurations that optimize space and aesthetics.
Scenario: Engineering Drawings
Engineers employ line geometry to create technical drawings, define the boundaries of components, and establish the relationships between different parts of a system.
Scenario: Cartography and Mapmaking
Cartographers use line geometry to represent geographic features, delineate boundaries, and create accurate maps that convey spatial information effectively.
FAQ's
The basic elements of line geometry include points, lines, and planes. A line is a straight path that extends infinitely in both directions and is represented by a straight line with two arrowheads.
In geometry, there are various types of lines, including horizontal lines, vertical lines, parallel lines, perpendicular lines, and intersecting lines. Each type of line exhibits unique properties and characteristics.
Lines play a crucial role in solving geometric problems by defining the boundaries of shapes, determining angles, and identifying the relationships between different geometric elements. They provide a framework for understanding the spatial relationships within a geometric system.
Parallel lines are lines that are always the same distance apart and never intersect. They have the property that corresponding angles are equal, alternate angles are equal, and the sum of interior angles on the same side of the transversal is 180 degrees.
Perpendicular lines intersect at right angles, forming 90-degree angles at the point of intersection. They have the property that the product of the slopes of two perpendicular lines is -1.
Like? Share it with your friends
Facebook
Twitter
LinkedIn