Converting Mixed Numbers to Improper Fractions

Introduction

Mixed Numbers and Improper Fractions

When dealing with fractions, the conversion of mixed numbers to improper fractions is a fundamental concept that plays a crucial role in simplifying mathematical operations and representing quantities in a standardized format. Let’s delve into the process of converting mixed numbers to improper fractions and explore its significance in various contexts.

Mixed Numbers

A mixed number is a number that combines a whole number and a fraction. For example, $3\frac{1}{2}$ is a mixed number where 3 is the whole number and $\frac{1}{2}$ is the fractional part. Mixed numbers are often used to express quantities that are more than one whole but not complete whole numbers, making them useful in everyday contexts like measurements, recipes, and time.

Improper Fractions

An improper fraction is a fraction where the numerator (the top number) is greater than or equal to the denominator (the bottom number). This means the fraction represents a value equal to or greater than one whole. For example, $\frac{7}{4}$ is an improper fraction because 7 is greater than 4.

Analogy of Definition

Mixed Numbers to Improper Fractions

Converting mixed numbers to improper fractions involves transforming a quantity expressed as a whole number and a proper fraction into a single fraction with a numerator that is greater than or equal to the denominator. This conversion allows for uniform representation and facilitates mathematical computations.

Method

How to Convert Mixed Fractions to Improper Fractions

There are several methods to convert a mixed number to an improper fraction. One approach involves multiplying the whole number by the denominator of the fraction and adding the numerator to obtain the new numerator, while retaining the original denominator.

Let’s convert $2\frac{3}{4}$ to an improper fraction.

Step 1: Multiply the whole number (2) by the denominator (4)

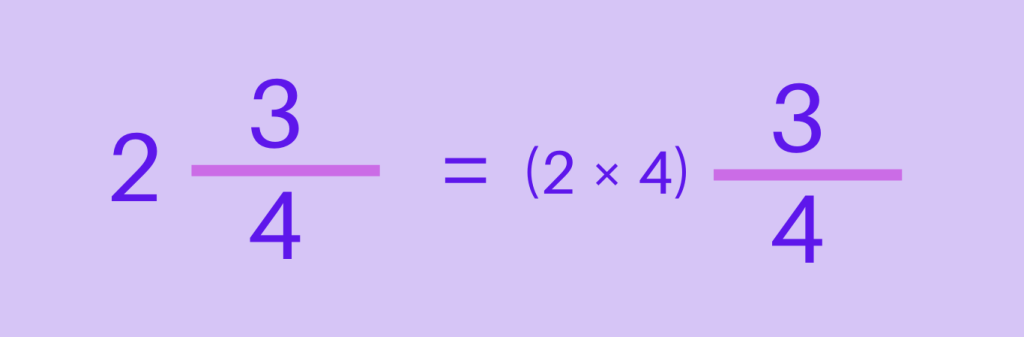
Step 2: Add the numerator (3) to this product.

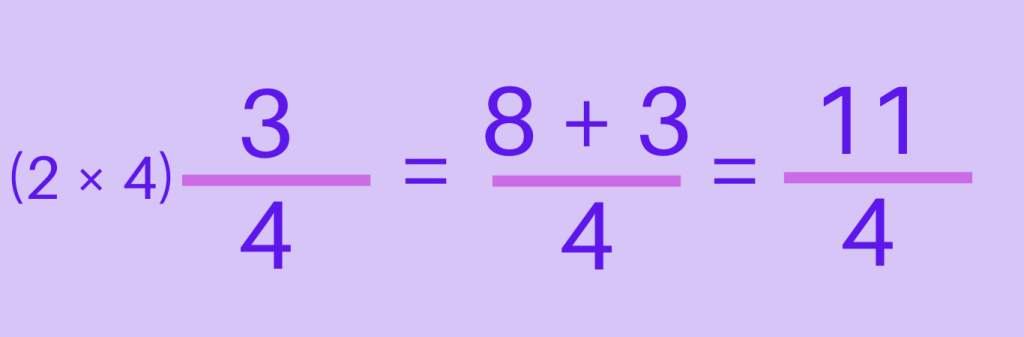
Step 3: Write the result as a fraction with the original denominator.

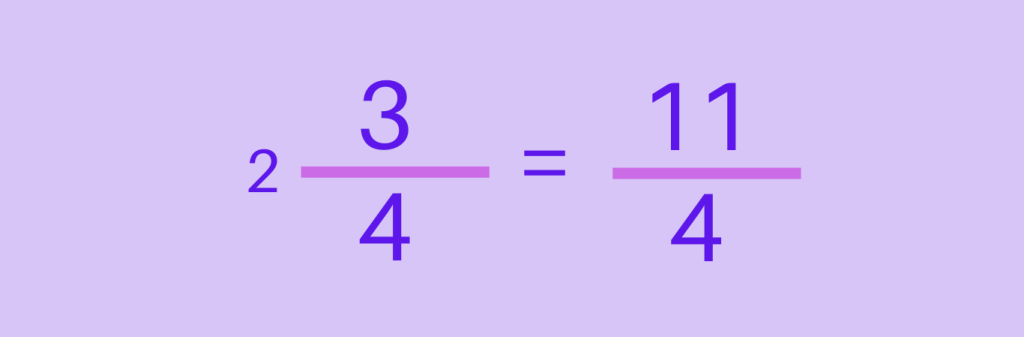
Examples

Converting $5\frac{2}{3}$ to an Improper Fraction:

Step 1: Multiply the whole number (5) by the denominator (3) and add the numerator (2) to obtain the new numerator: 3 × 5 + 2= 17.
Step 2: Retain the original denominator (3).
Therefore, $5\frac{2}{3}$ as an improper fraction is $\frac{17}{3}$ .

Summary:
This example illustrates the process of converting the mixed number 2 3/4 to an improper fraction. By multiplying the whole number by the denominator and adding the numerator, the mixed number is transformed into the improper fraction 11/4. This conversion simplifies the representation of the quantity and enables seamless mathematical operations.

Quiz

Tips and Tricks

1. Multiplication Method

Tip: To convert a mixed number to an improper fraction using the multiplication method, multiply the whole number by the denominator and add the numerator to obtain the new numerator. Retain the original denominator.

2. Addition Method

Tip: Utilize the addition method by adding the product of the whole number and the denominator to the numerator to obtain the new numerator. Retain the original denominator.

3. Visual Representation

Tip: Use number lines or area models to visually represent the conversion of a mixed number to an improper fraction.

Real life application

Scenario: Baking a Cake

When following a baking recipe that calls for $2\frac{1}{2}$ cups of flour, converting the mixed number to an improper fraction $\frac{5}{2}$ allows for precise measurement and adjustment of ingredients.

Scenario: Construction Project
In construction projects, converting mixed measurements to improper fractions facilitates accurate calculations and comparisons of dimensions, contributing to the precision and quality of the construction work.

FAQ's

What is the significance of converting mixed numbers to improper fractions?

Converting mixed numbers to improper fractions is important as it allows for easier mathematical operations such as addition, subtraction, multiplication, and division. It also provides a standardized format for comparing and ordering fractions.

How is a mixed number different from an improper fraction?

A mixed number consists of a whole number and a proper fraction, while an improper fraction has a numerator that is greater than or equal to the denominator.

Can you provide an example of converting a mixed number to an improper fraction?

Certainly! Converting the mixed number 3 1/2 to an improper fraction yields the result 7/2. This transformation involves multiplying the whole number by the denominator of the fraction and adding the numerator to obtain the new numerator, while retaining the original denominator.

What methods can be used to convert a mixed number to an improper fraction?

There are multiple methods to convert a mixed number to an improper fraction, including the multiplication method, the addition method, and the visual representation method using number lines or area models.

How is the concept of converting mixed numbers to improper fractions applied in real-life situations?

The concept of converting mixed numbers to improper fractions finds practical applications in various real-life scenarios such as cooking recipes, measurements, and construction projects where precise calculations and comparisons are essential.

Like? Share it with your friends