Mastering the Art of Multiplying Fractions
Table of Contents
Introduction
Multiplying Fractions
Multiplying fractions is a fundamental concept in mathematics that involves combining two or more fractional quantities to find their product. Whether dealing with proper fractions, improper fractions, mixed numbers, or whole numbers, understanding the rules of multiplication for fractions is essential for solving a wide range of mathematical problems.
Analogy of Definition
The Rules of Multiplication
When multiplying fractions, the key rule to remember is to multiply the numerators together to get the new numerator, and multiply the denominators together to get the new denominator. For mixed fractions, we have to first convert it into proper or improper fraction , and then multiply it.
Method
Multiplying Fractions with Same Denominator
To multiply two proper fractions, simply multiply the numerators to get the new numerator, and multiply the denominators to get the new denominator.
For example, lets take \frac{5}{3}and \frac{2}{3} We will begin by multiplying the numerator and the denominator separately. \frac{5*2}{3*3}. We will get the product of \frac{10}{9}.
Multiplying Fractions with Different Denominators
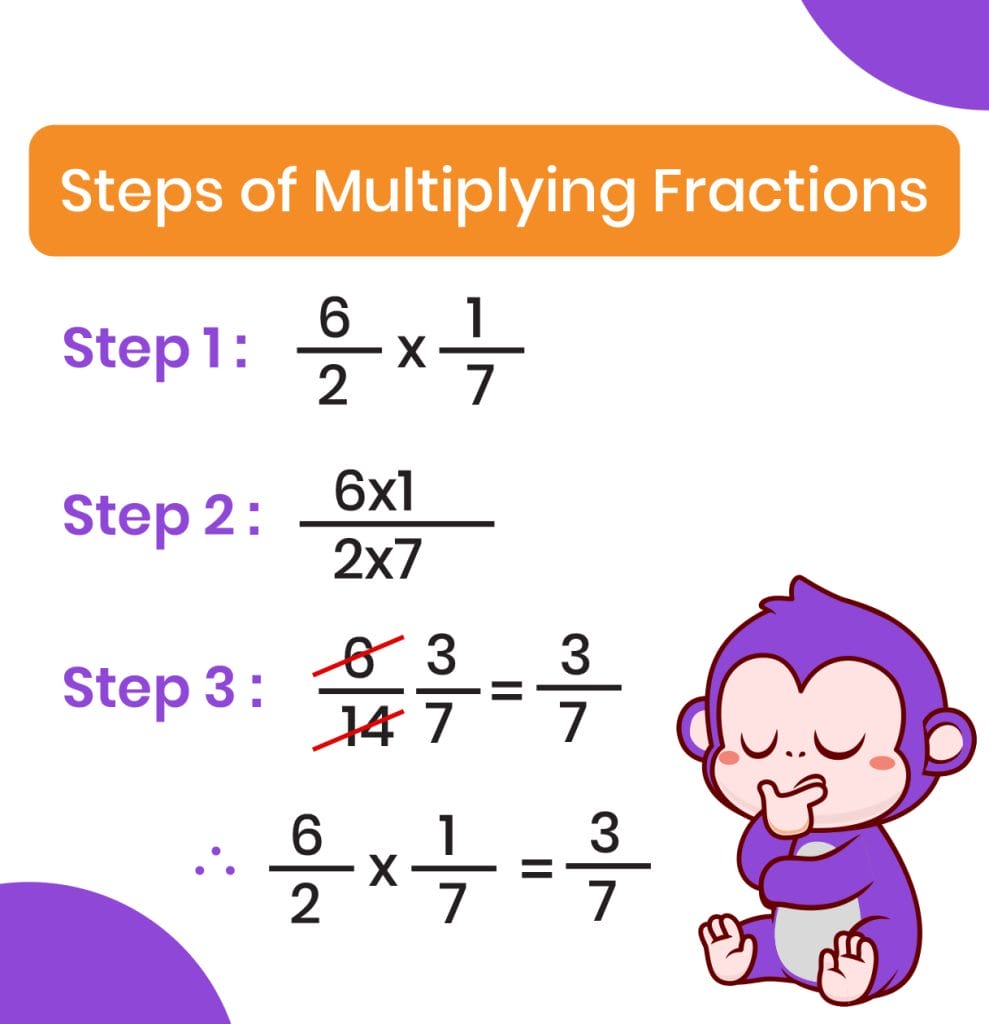
When multiplying two improper fractions, we follow the same rule of multiplying the numerators to get the new numerator, and multiplying the denominators to get the new denominator.
For example, to multiply\frac{6}{2} and \frac{1}{7}, we will multiply the numerators and denominators, \frac{6*1}{2*7}. The product will be \frac{6}{14}. It can be simplified into \frac{3}{7}.
Multiplying Fractions with Mixed Numbers
To multiply a fraction with a mixed number, convert the mixed number to an improper fraction, then follow the rule of multiplying the numerators and denominators.
For example, to multiply 2\frac{1}{4} and \frac{3}{5}, first we will convert 2\frac{1}{4} into an improper fraction. Converting 2\frac{1}{4} to improper fraction will be \frac{9}{4}. Now, we will multiply \frac{9}{4} and \frac{3}{5}. Thus, the product will be \frac{27}{20}
Multiplying Fractions by Whole Numbers
When multiplying a fraction by a whole number, simply multiply the whole number by the numerator of the fraction, and keep the denominator the same. For example, to multiply 3/4 by 5, the product would be (3*5)/4 = 15/4.
Examples
Multiplying Fractions Examples
Example 1: Multiplying 2/3 and 3/4
Step 1: Multiply the numerators: 2 * 3 = 6
Step 2: Multiply the denominators: 3 * 4 = 12
Product: 6/12, which simplifies to 1/2
Example 2: Multiplying 7/5 and 4/3
Step 1: Multiply the numerators: 7 * 4 = 28
Step 2: Multiply the denominators: 5 * 3 = 15
Product: 28/15
Quiz
Tips and Tricks
1. Multiplying fraction and whole number.
Tip: To multiply a fraction by a whole number, simply multiply the whole number by the numerator of the fraction, and keep the denominator the same.
Calculation: (2/3) * 4 = (2*4)/3 = 8/3
2. Multiplying mixed fraction with wh0le number.
Tip: To multiply a mixed number by a whole number, convert the mixed number to an improper fraction, then multiply the numerators and denominators.
Calculation: 2\frac{1}{2} * 3 = (5/2) * 3 = 15/2 = 7 1/2
3. Multiplying fractions after simplifying
Tip: We can first simply the fractions and then go along with the multiplication.
Calculation: \frac{1}{4} * \frac{8}{4} = \frac{1}{1} * \frac{2}{4} = \frac{2}{4} = \frac{1}{2}
Real life application
Story: “The Fractional Adventures of Emma and Noah”
Emma and Noah were two adventurous friends who loved exploring the world of fractions. As they encountered various real-life scenarios, they applied their knowledge of multiplying fractions to solve practical problems and make informed decisions.
Challenge 1: The Pizza Party Planning
Emma and Noah were planning a pizza party for their friends. Each person would eat 2/3 of a pizza, and they had 4 pizzas. To calculate the total number of pizzas needed, they multiplied (2/3) * 4, which resulted in 8/3, indicating that 8/3 pizzas would be consumed.
Challenge 2: The Baking Extravaganza
As they prepared to bake a special recipe, Emma and Noah needed to calculate the total amount of flour required. With each batch needing 3/4 cup of flour, and 4 batches to be made, they multiplied (3/4) * 4, resulting in 12/16 cups of flour needed.
Challenge 3: The Gardening Project
In their gardening project, Emma and Noah had to determine the total length of the rows in their garden. Each row was 1/2 feet long, and there were 3 rows. By multiplying (1/2) * 3, they found that the total length of the rows would be 3/2 feet.
FAQ's
The key rule for multiplying fractions is to multiply the numerators together to get the new numerator, and multiply the denominators together to get the new denominator. This rule applies to proper fractions, improper fractions, mixed numbers, and whole numbers.
To multiply two proper fractions, simply multiply the numerators to get the new numerator, and multiply the denominators to get the new denominator.
The rule for multiplying improper fractions is the same as for proper fractions. Multiply the numerators to get the new numerator, and multiply the denominators to get the new denominator.
To multiply a fraction with a mixed number, convert the mixed number to an improper fraction, then follow the rule of multiplying the numerators and denominators.
Common mistakes when multiplying fractions include forgetting to simplify the result, multiplying the denominators instead of the numerators, and not converting mixed numbers to improper fractions before multiplication. Hence, one should be mindful about these mistakes while multiplying fractions.
Like? Share it with your friends
Facebook
Twitter
LinkedIn