Mastering the Art of Multiplying Mixed Fractions
Table of Contents
Introduction
Mixed Fractions
In the realm of mathematics, mixed numbers are a combination of whole numbers and fractions. They are represented as a whole number followed by a fraction, such as 3\frac{1}{2}. When it comes to multiplication, understanding how to multiply mixed fractions is a crucial skill that can be applied in various mathematical scenarios.
Analogy of Definition
Multiplying Mixed Fraction by a Fraction
When multiplying a mixed number by a fraction, the process involves converting the mixed number into an improper fraction, multiplying the two fractions, and then simplifying the result. Let’s explore the step-by-step method of multiplying a mixed number by a fraction to achieve accurate solutions.
Multiplying Two Mixed Numbers
When faced with the task of multiplying two mixed numbers, the approach involves converting each mixed number into an improper fraction, multiplying the two fractions, and simplifying the resulting product. This process allows for the accurate calculation of the product of two mixed numbers.
Method
Multiplying Mixed Fractions
Step 1: Convert the mixed numbers to improper fractions
Let’s multiply the numbers: 3\frac{1}{2} with 2\frac{2}{3}
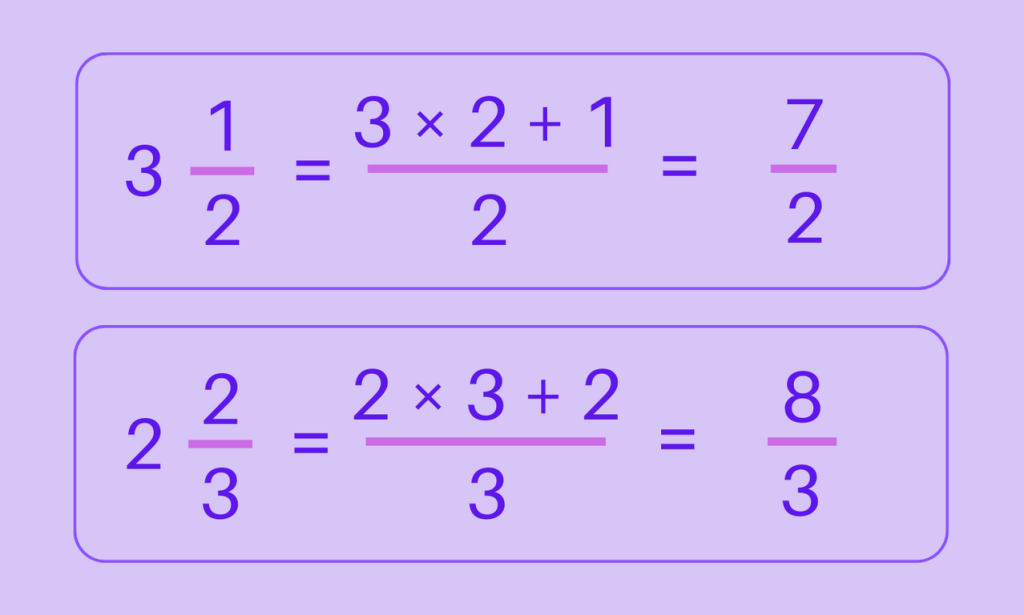
Step 2: Multiply the two fractions
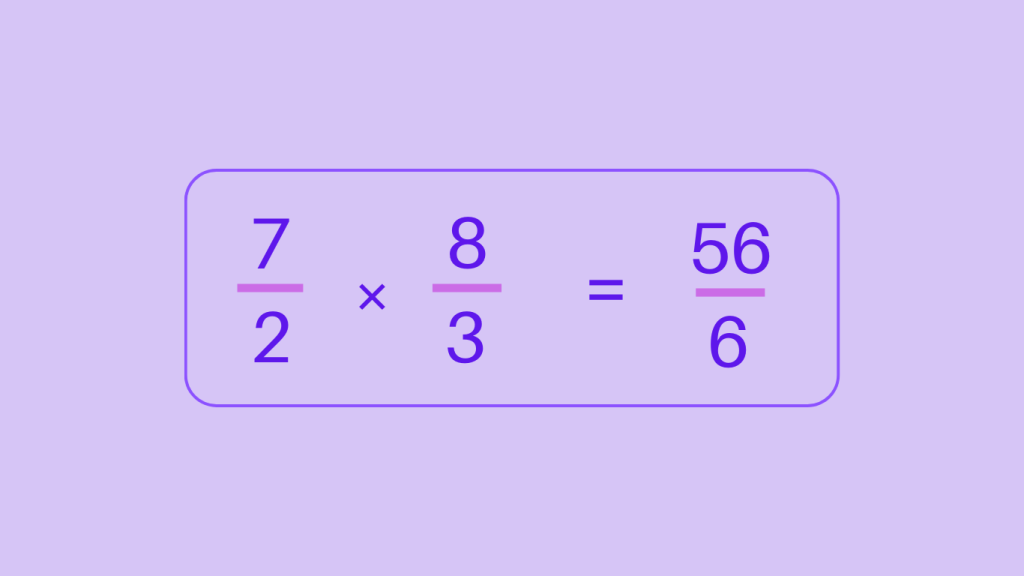
Step 3: Simplify the resulting product
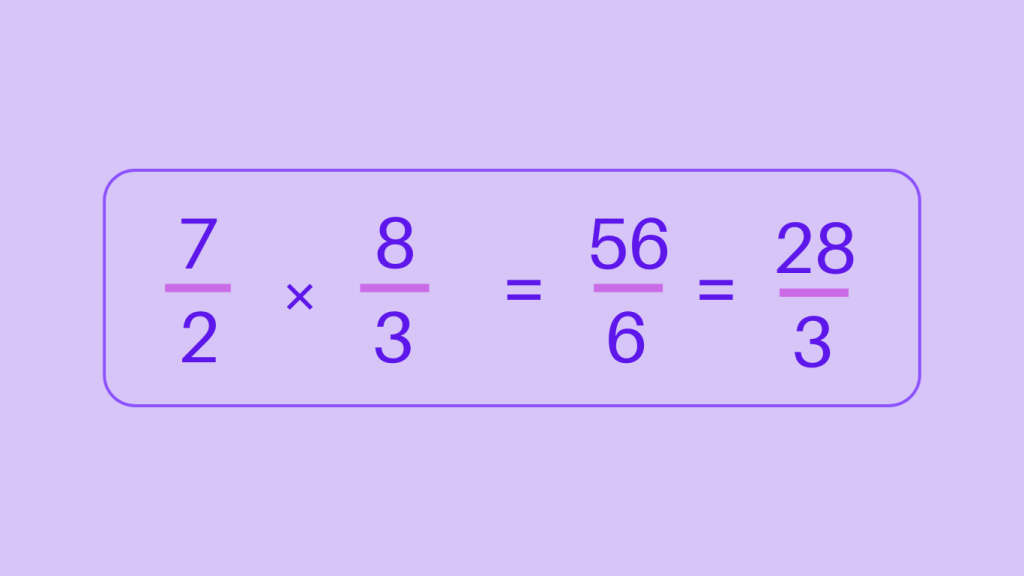
So, the product of 3\frac{1}{2} and 2\frac{2}{3} is \frac{28}{3}.
Examples
Multiplying Mixed Fractions Example
Example 1: Multiply 4\frac{1}{4} and 3\frac{3}{5}
Step 1: Convert the mixed numbers to improper fractions
4\frac{1}{4} = \frac{(4 × 4 + 1)}{4} = \frac{(17}{4}
3\frac{3}{5} = \frac{(3 × 5 + 3)}{5} = \frac{(18}{5}
Step 2: Multiply the two fractions
\frac{17}{4} × \frac{18}{4} = \frac{306}{20}
Step 3: Simplify the resulting product
\frac{306}{20} = \frac{153}{10}
Hence, the product is \frac{153}{10}
Quiz
Tips and Tricks
1. Convert to Improper Fractions
Tip: Before multiplying, convert the mixed fractions to improper fractions. Multiply the whole number by the denominator and add the numerator, then keep the same denominator.
2. Multiply Numerators and Denominators
Tip: Once you have two improper fractions, simply multiply the numerators together to get the new numerator, and multiply the denominators together to get the new denominator.
3. Simplify if Possible
Tip: After multiplying, simplify the resulting fraction if possible by reducing it to its simplest form.
4. Use Common Denominators for Addition or Subtraction
Tip: If you’re adding or subtracting mixed fractions after multiplication, ensure they have a common denominator.
5. Practice with Examples
Tip: Practice multiplying mixed fractions with different examples to get comfortable with the process.
Real life application
Story: “The Multiplication Adventures of Maya and Ethan”
Maya and Ethan, two young mathematicians, embarked on a series of multiplication adventures that showcased the practical applications of multiplying mixed fractions in real-life scenarios.
Adventure 1: The Cooking Challenge
Maya and Ethan were tasked with preparing a special recipe that required 3 1/2 cups of flour. To cater to a larger group, they needed to triple the recipe. By applying the concept of multiplying a mixed number by a fraction, they accurately calculated that 3 1/2 cups of flour would triple to 10 1/2 cups, ensuring the success of their culinary endeavor.
Adventure 2: The Construction Project
In another adventure, Maya and Ethan were involved in a construction project that required 4 1/2 tons of gravel per day. By multiplying the mixed number representing the amount of gravel needed by the number of days, they determined the total amount of gravel required for the project, showcasing the practicality of multiplying two mixed numbers in real-world applications.
Adventure 3: The Art of Baking
As part of a baking challenge, Maya and Ethan were tasked with creating a series of pizzas, each requiring 1 3/4 cups of cheese. By multiplying the mixed number representing the amount of cheese per pizza by the total number of pizzas, they accurately calculated the total amount of cheese needed, demonstrating the relevance of multiplying mixed fractions in culinary endeavors.
FAQ's
The key steps to multiply mixed fractions involve converting each mixed number into an improper fraction, multiplying the two fractions together, and simplifying the resulting product to obtain the accurate solution.
When multiplying a mixed number by a fraction, the mixed number is first converted into an improper fraction. The resulting improper fraction is then multiplied by the given fraction, and the product is simplified to obtain the final result.
Multiplying two mixed numbers is essential in various real-life scenarios, such as cooking, construction, and crafting, where accurate calculations of quantities and measurements are required for successful outcomes.
Yes, the concept of multiplying mixed fractions has practical applications in everyday tasks, including cooking, baking, construction projects, and artistic endeavors, where accurate measurements and calculations are essential for achieving desired results.
Understanding the process of multiplying mixed fractions enhances problem-solving skills by enabling individuals to accurately calculate quantities, measurements, and proportions in various real-life and mathematical scenarios, leading to effective solutions.
Like? Share it with your friends
Facebook
Twitter
LinkedIn