Understanding Parallel Lines: Definition and Properties
Table of Contents
Introduction
Parallel Lines
Parallel lines are a fundamental concept in geometry, playing a crucial role in various mathematical and real-world contexts. Let’s delve into the realm of parallel lines, exploring their definition, properties, and practical significance.
Analogy of Definition
What are Parallel Lines?
Parallel lines refer to two or more lines that maintain a constant distance from each other and never intersect. They extend infinitely in both directions and have the same slope. Parallel lines are represented by the symbol “//”.
In the figure below, line “AB” is parallel to the line”CD”, it can also be represented as AB // CD.
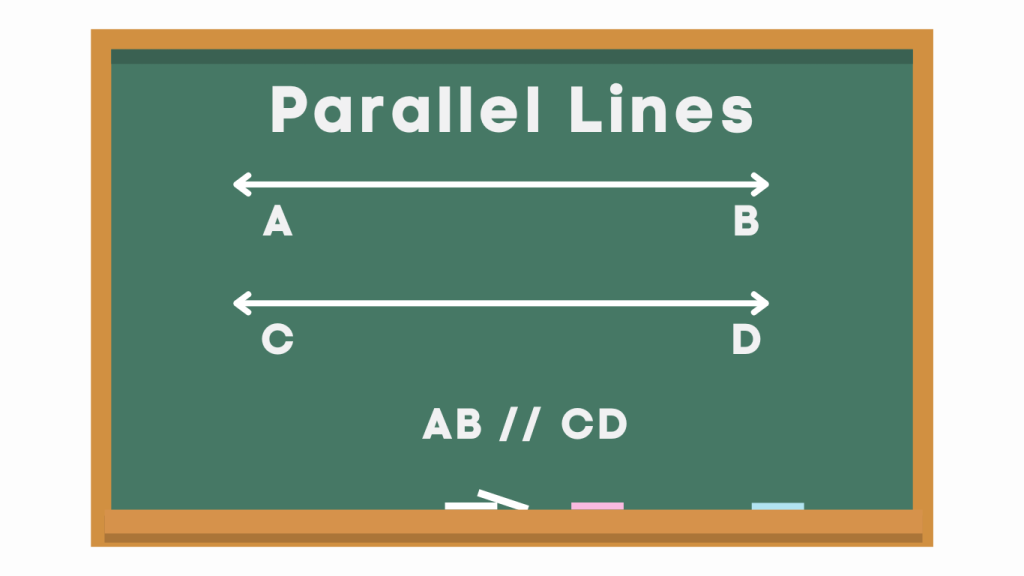
We can also identify parallel lines in different shapes. Typically, within a shape, if the lines are parallel, it is denoted by an arrow like symbol.
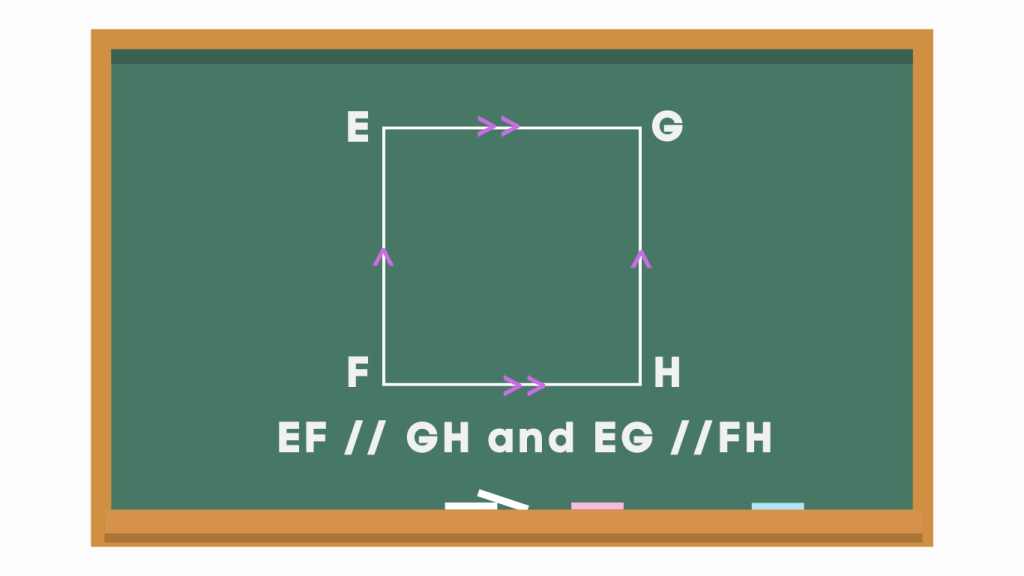
Method
Properties of Parallel Lines
1. Never Intersect: Parallel lines are lines that are always the same distance apart and never intersect, even if extended infinitely in both directions.
2. Constant Distance: The distance between parallel lines remains constant throughout their length. This property is essential for various applications, such as constructing shapes and determining distances.
3. Equal Slopes: Parallel lines have equal slopes. In other words, if the slope of one line is 𝑚, then the slope of the other parallel line is also 𝑚.
4. No Common Points: Parallel lines do not share any common points. They maintain a consistent distance apart from each other along their entire length.
5. Transitive Property: If two lines are parallel to the same line, they are parallel to each other. This property allows for the identification of parallel lines based on their relationship to a third line.
Transversal Line
A transversal line is a line that intersects two or more other lines at distinct points. Imagine you have two or more straight lines, and then you draw another line that crosses them. That line you drew is called a transversal line. It’s like a bridge that goes over two roads or rivers.
Transversal lines are important in geometry because they help us study the relationships between angles formed by intersecting lines. They create various types of angles like corresponding angles, alternate interior angles, alternate exterior angles, and consecutive interior angles, which have specific properties and relationships.
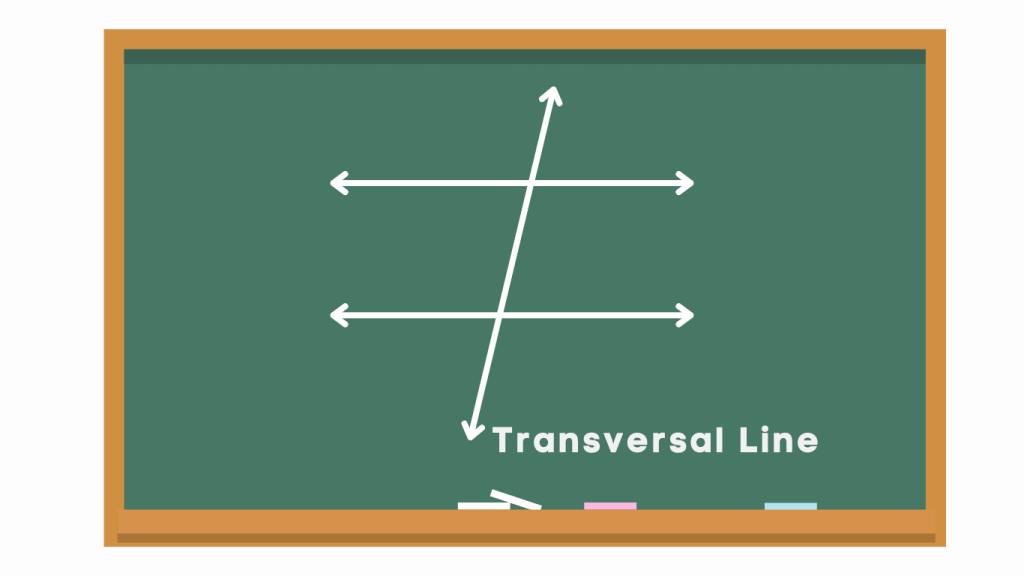
Parallel Lines and Transversal
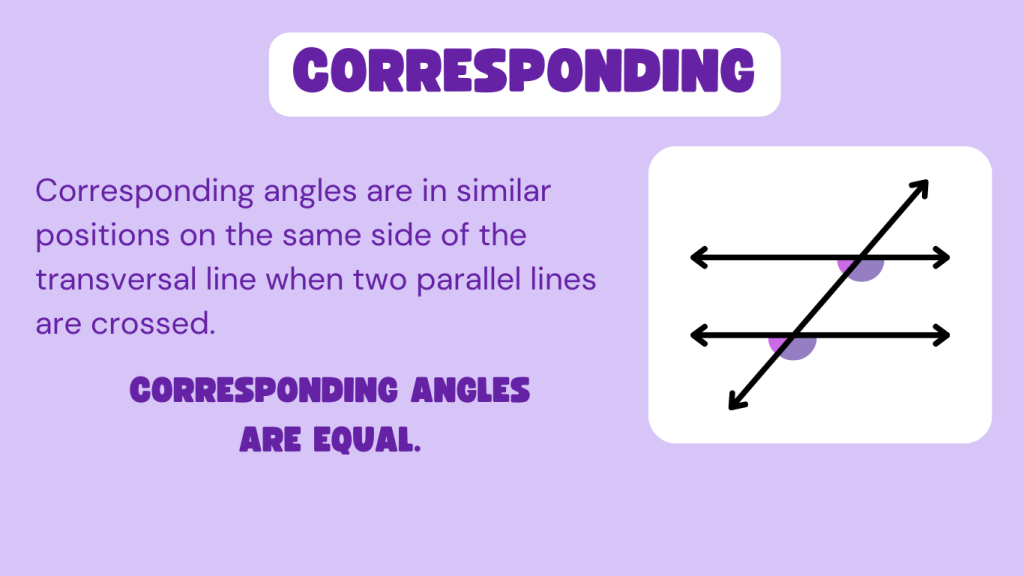
1. Corresponding Angles
Corresponding angles are in matching positions on the same side of the transversal. They are equal in measure if the lines are parallel.
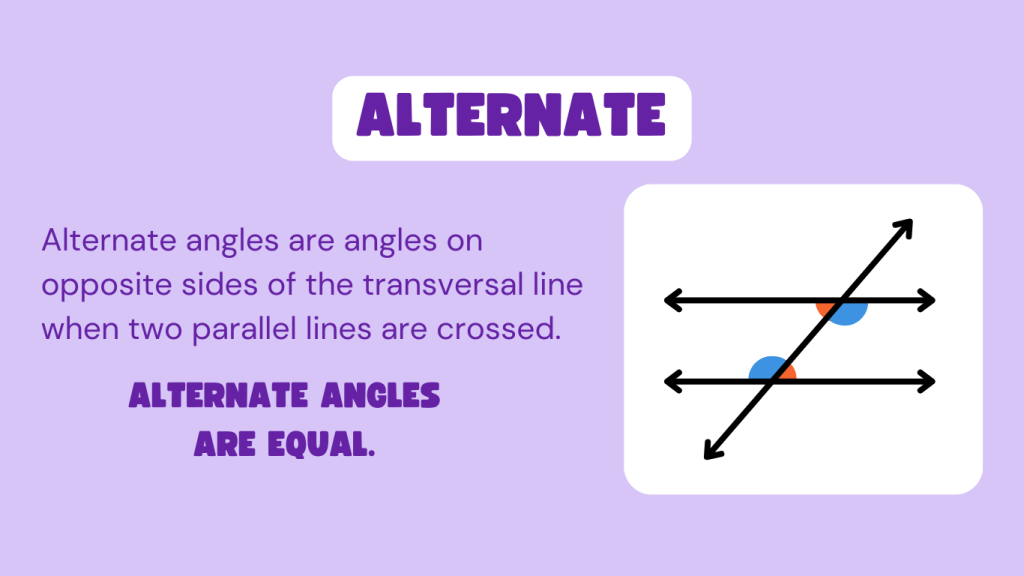
2. Alternate Angles
Alternate interior angles are on opposite sides of the transversal and inside the parallel lines. They are equal in measure if the lines are parallel.
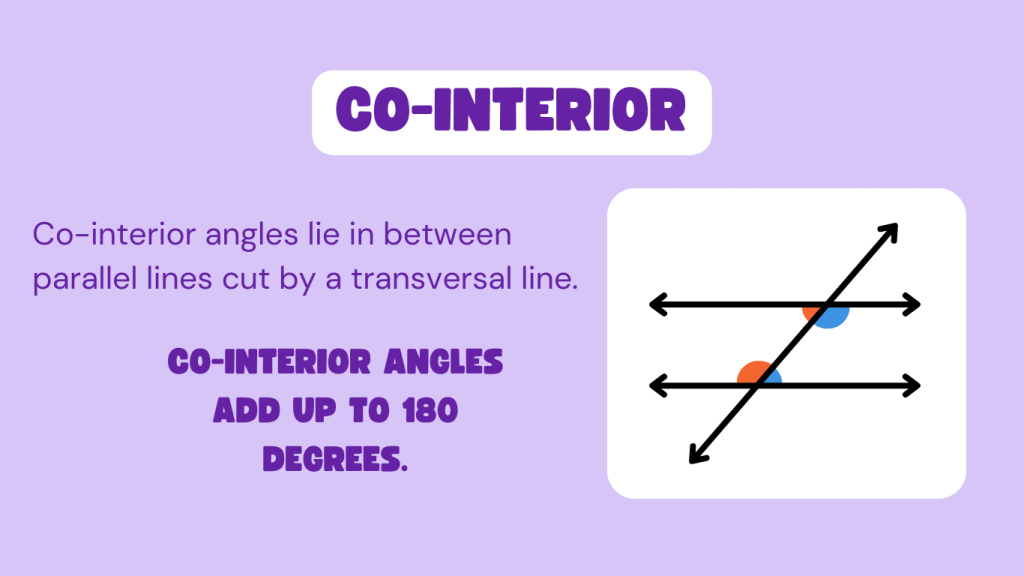
3. Consecutive Interior Angles:
Co-interior angles are also on the same side of the transversal and inside the parallel lines, but they are adjacent to each other rather than being across from each other. Co-interior angles are supplementary, meaning their measures add up to 180 degrees if the lines are parallel.
Examples
Summary: This example illustrates the process of identifying parallel lines by comparing their slopes. In this scenario, the equations y = 2x + 3 and y = 2x – 1 are found to be parallel due to their equal slopes of 2.
Quiz
Tips and Tricks
1. Equal Angles
Tip: When a transversal intersects two parallel lines, corresponding angles are equal. So, if you can identify a pair of corresponding angles, you can determine if the lines are parallel.
2. Identify Transversals
Tip: Look for lines that intersect two or more other lines. These are transversal lines, and they can help you identify parallel lines and determine angle relationships.
3. Check for Equal Slopes
Tip: If you have the equations of two lines and want to know if they are parallel, compare their slopes. Parallel lines have equal slopes.
4. Use a Protractor
Tip: If you can measure angles, look for pairs of alternate interior angles or corresponding angles. If they are equal, the lines are parallel.
Real life application
Scenario: In architecture, parallel lines are utilized to create precise floor plans and structural designs. Engineers use the concept of parallel lines to ensure accurate alignments and measurements in construction projects.
FAQ's
Parallel lines are two or more lines that are always the same distance apart and never intersect. They have the same slope and will never converge.
Understanding parallel and perpendicular lines is crucial in geometry and real-world applications. It helps in solving problems related to angles, shapes, and spatial relationships.
Parallel lines can be identified by checking if they have the same slope. If the slopes are equal, the lines are parallel.
The properties of parallel lines include never intersecting, having the same slope, and always being equidistant from each other.
Parallel lines have practical applications in architecture, engineering, and design, where precise measurements and alignments are essential.
Like? Share it with your friends
Facebook
Twitter
LinkedIn