How to Find the Perimeter of Polygons? – Formulas and Examples
Table of Contents
Introduction
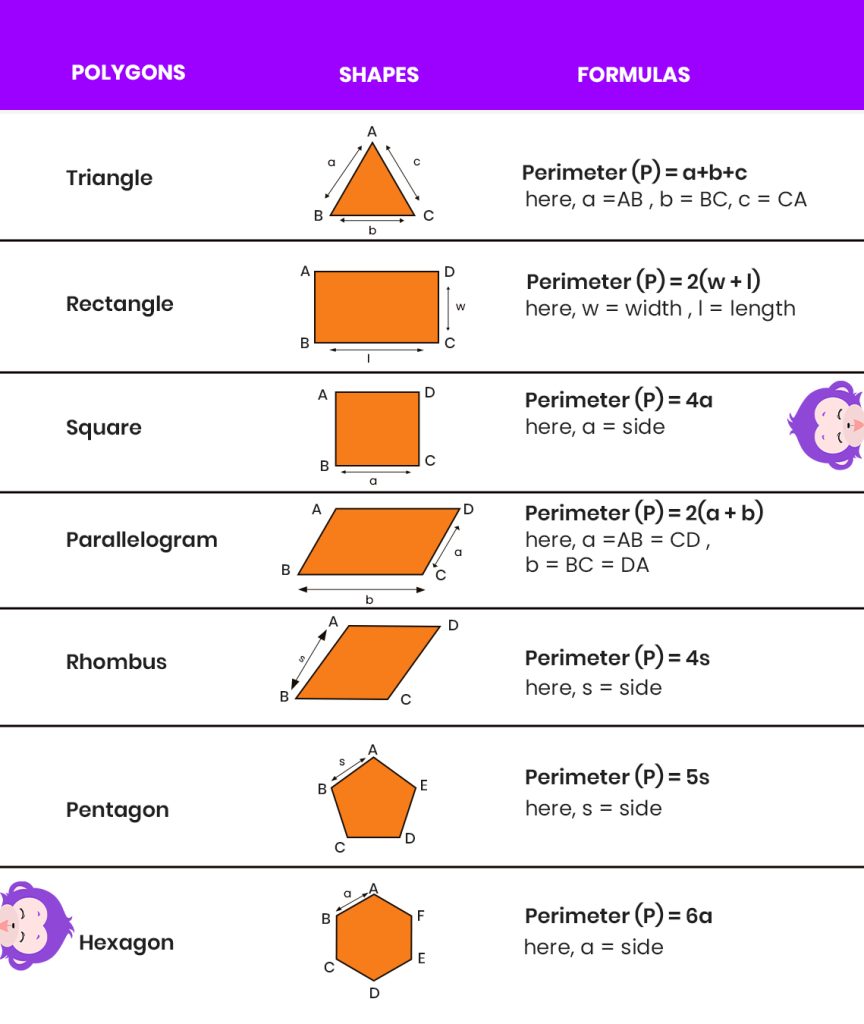
Perimeter of Polygons
In the realm of geometry, the concept of perimeter of polygons plays a crucial role in determining the total length of the boundary of a shape. When it comes to polygons, the calculation of perimeter of polygins becomes essential in various mathematical and real-world scenarios. Let’s delve into the world of polygons and understand the significance of their perimeters.
Analogy of Definition
What is Perimeter of Polygons?
The perimeter of a polygon is the total distance around the outside of the shape. It is calculated by adding the lengths of all the sides of the polygon. Whether it’s a regular polygon with equal sides and angles or an irregular polygon with varying side lengths and angles, the perimeter provides a comprehensive measure of the shape’s boundary.
Method
Calulating Perimeter of Polygons
The formula for finding the perimeter of a polygon depends on the type of polygon. For a regular polygon, the perimeter can be calculated by multiplying the number of sides (n) by the length of each side (s). The formula is given as:
For an irregular polygon, the perimeter is determined by adding the lengths of all the sides together. Irregular Polygons refer to those polygons in which neither are the lengths equal nor the angles.
Some common formulas for finding out the perimeter of polygons are given below.
Examples
Finding the Perimeter of Polygon
Example 1 – Finding the perimeter of Hexagon with lenggth of each side equal to 8 cm.
Step 1: Identify the number of sides (n) and the length of each side (s)
For a regular hexagon, n = 6 (number of sides) and given length of side (s) = 8 cm
Step 2:Apply the formula for the perimeter of a regular polygon
Perimeter = n * s
Perimeter = 6 * 8
Perimeter = 48 cm
So, the perimeter of the regular hexagon is 48 cm.
Example 2: Perimeter of Irregular Polygon
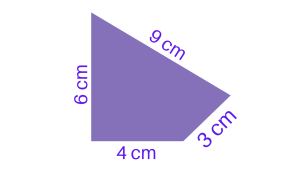
To find out the perimeter of the figure, we will have to add the length of all sides,
Perimeter of polygon = (6 + 4 + 3 + 9) cm = 22 cm
Quiz
Tips and Tricks
- Formula of Perimeter of Polygon
Tip: For a regular polygon, use the formula Perimeter = n * s, where n is the number of sides and s is the length of each side.
Calculation: Perimeter of a regular pentagon with n = 5 and s = 12
Perimeter = 5 * 12
Perimeter = 60 units - The Irregular Polygon Perimeter Calculation
Tip: For an irregular polygon, add the lengths of all the sides to find the perimeter.
Calculation: Perimeter of an irregular hexagon with side lengths 8, 10, 12, 15, 18, and 20
Perimeter = 8 + 10 + 12 + 15 + 18 + 20
Perimeter = 83 units - The Perimeter of a Regular Octagon
Tip: For a regular octagon, calculate the perimeter by multiplying the number of sides by the length of each side.
Calculation: Perimeter of a regular octagon with n = 8 and s = 14
Perimeter = 8 * 14
Perimeter = 112 units - The Perimeter of an Irregular Quadrilateral
Tip: For an irregular quadrilateral, simply add the lengths of all the sides to determine the perimeter.
Calculation: Perimeter of an irregular quadrilateral with side lengths 6, 8, 10, and 12
Perimeter = 6 + 8 + 10 + 12
Perimeter = 36 units - The Perimeter of a Regular Decagon
Tip: For a regular decagon, use the formula Perimeter = n * s, where n is the number of sides and s is the length of each side.
Calculation: Perimeter of a regular decagon with n = 10 and s = 9
Perimeter = 10 * 9
Perimeter = 90 units
Real life application
Story: “Maya and Ethan Find the Perimeter of Polygon”
Maya and Ethan, two young explorers, embarked on a quest that led them to various challenges where the concept of perimeter of polygon played a crucial role in their success.
Challenge 1: The Maze Escape
In their adventure, Maya and Ethan encountered a mysterious maze with irregular polygon-shaped walls. To find their way out, they had to calculate the perimeter of the maze and identify the shortest path. By adding the lengths of the sides, they determined the total perimeter and successfully navigated through the maze.
Challenge 2: The Treasure Map
As they ventured further, Maya and Ethan discovered a treasure map that led them to a hidden cave. The map indicated the location of the treasure within a regular hexagon-shaped area. By calculating the perimeter of the hexagon, they determined the boundary of the treasure site and uncovered the hidden riches.
Challenge 3: The Bridge Crossing
In their final challenge, Maya and Ethan encountered a series of bridges with irregular polygon-shaped arches. To cross safely, they needed to calculate the perimeter of each bridge arch and identify the sturdiest path. By applying their knowledge of perimeter, they successfully crossed the bridges and completed their quest.
FAQ's
The formula for the perimeter of polygon is given by Perimeter = n * s, where n is the number of sides and s is the length of each side.
To find the perimeter of an irregular polygon, simply add the lengths of all the sides together to determine the total boundary length of the shape.
Calculating the perimeter of polygons is essential in various real-life scenarios such as measuring the boundary of land plots, designing fences, determining the length of paths, and navigating through mazes or obstacle courses.
Yes, the perimeter of polygon can also be calculated using the formula Perimeter = n * a, where n is the number of sides and a is the apothem (distance from the center to the midpoint of a side).
In architecture and construction, the concept of perimeter is used to determine the total length of building structures, the layout of rooms, the design of pathways, and the allocation of materials for construction projects.
By exploring the concept of perimeter of polygons, we gain a deeper understanding of how this fundamental geometric measure influences various aspects of our lives. Whether it’s solving mathematical puzzles, navigating through challenges, or designing real-world structures, the concept of perimeter remains an essential tool in our journey of exploration and discovery.
Like? Share it with your friends
Facebook
Twitter
LinkedIn