Perimeter of Triangle – Formulas and Examples
Table of Contents
Introduction
Perimeter of Triangle
The concept of perimeter of triangle is svery important which we must understand. The concept of perimeter is a fundamental aspect of geometry, and when it comes to triangles, understanding the perimeter is essential. In this article, we will delve into the world of triangles and explore the various methods for calculating their perimeters.
Analogy of Definition
What is Perimeter of Triangle?
The perimeter of a triangle is the total distance around the outside of the triangle. It is calculated by adding the lengths of all three sides of the triangle. The perimeter is a crucial measurement that helps determine the total length of the boundary of a polygon.
Method
Calculating Perimeter of Triangle
There are different types of triangles, such as equilateral, isosceles, and scalene, and each type has its own formula for calculating the perimeter.
Perimeter of Triangle: Equilateral Triangle: In an equilateral triangle, all three sides are of equal length. The formula to calculate the perimeter of an equilateral triangle is P = 3s, where P is the perimeter and s is the length of one side.
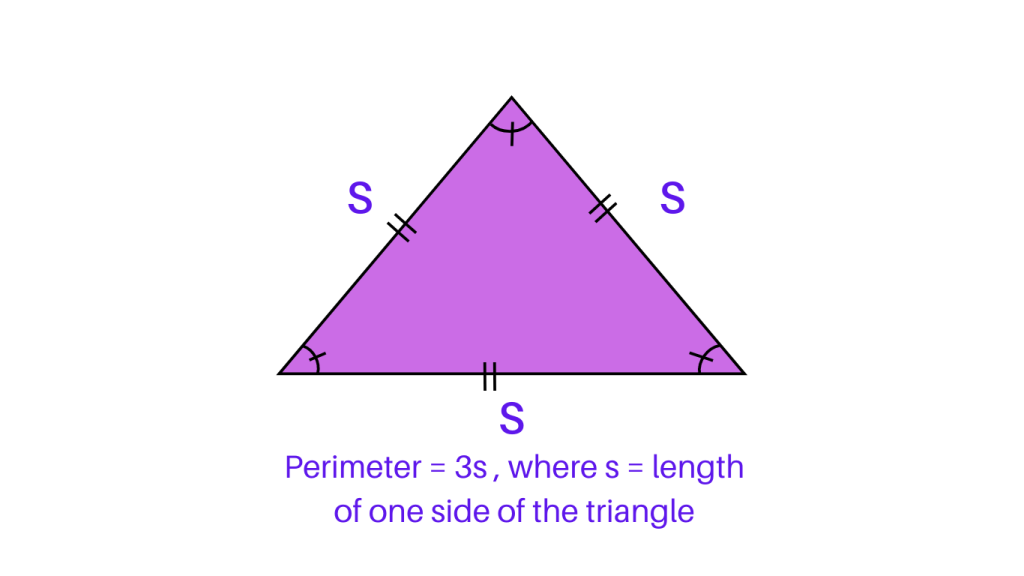
Perimeter of Triangle: Isosceles Triangle: An isosceles triangle has two sides of equal length. To find the perimeter of an isosceles triangle, the formula is P = 2a + b, where P is the perimeter, a is the length of the equal sides, and b is the length of the unequal side.
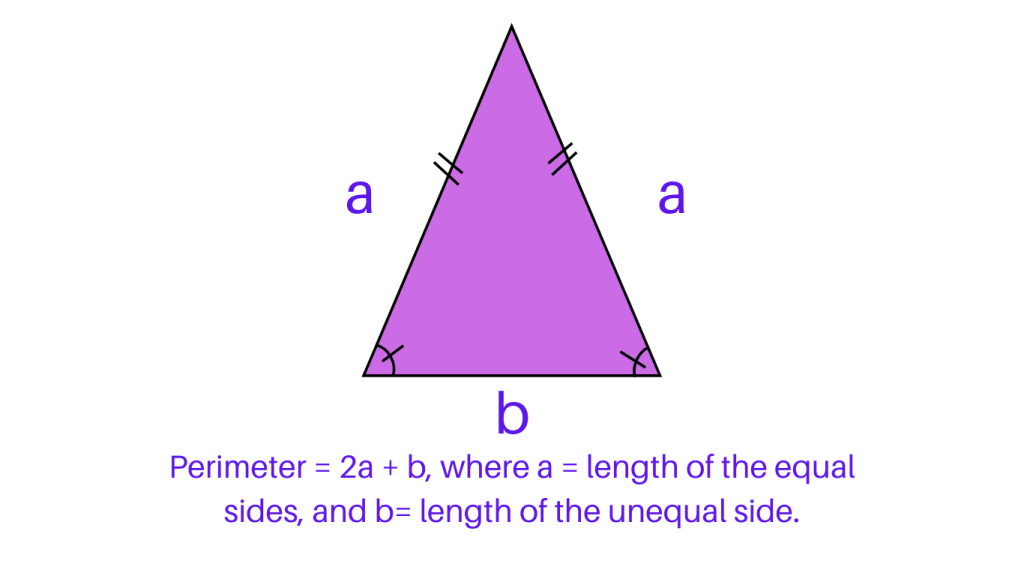
Perimeter of Triangle: Scalene Triangle: A scalene triangle has all three sides of different lengths. The perimeter of a scalene triangle is calculated by adding the lengths of all three sides, using the formula P = a + b + c, where P is the perimeter, and a, b, and c are the lengths of the three sides.
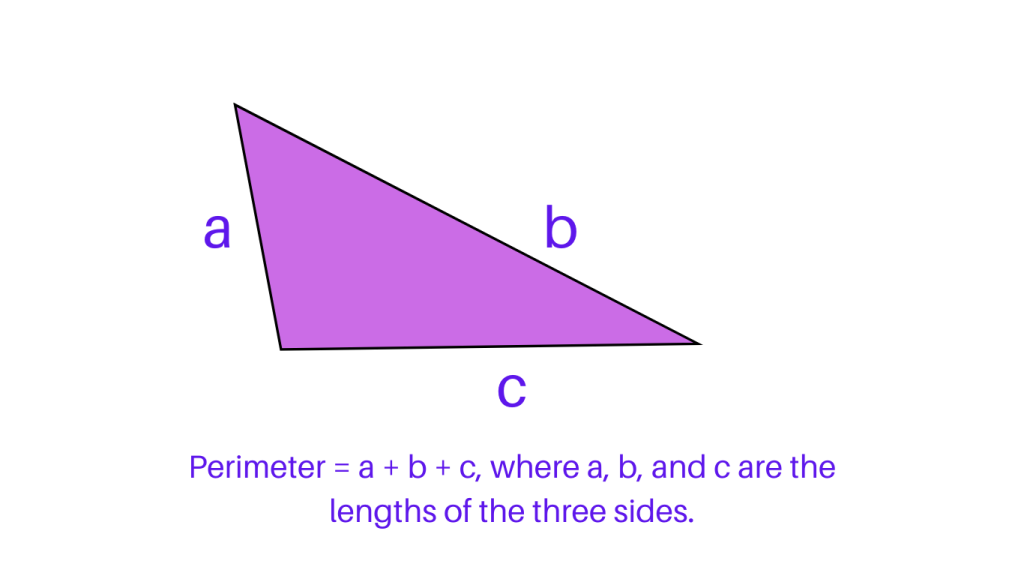
Want to learn more about triangle? Visit our site ChimpVine for interactive content related to triangles.
Examples
Finding the Perimeter of Triangles
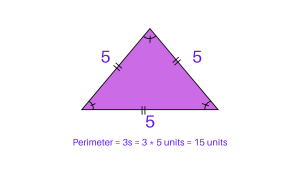
Example 1: Equilateral Triangle
Given the side length of an equilateral triangle as 5 units.
Using the formula P = 3s, where s = 5
P = 3 * 5
P = 15 units
The perimeter of the equilateral triangle is 15 units.
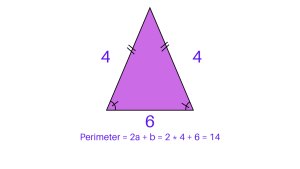
Example 2: Isosceles Triangle
Given the lengths of the equal sides as 4 units each and the length of the unequal side as 6 units.
Using the formula P = 2a + b, where a = 4 and b = 6
P = 2 * 4 + 6
P = 8 + 6
P = 14 units
The perimeter of the isosceles triangle is 14 units.
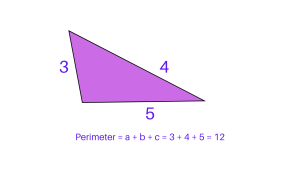
Example 3: Scalene Triangle
Given the lengths of the three sides as 3 units, 4 units, and 5 units.
Using the formula P = a + b + c, where a = 3, b = 4, and c = 5
P = 3 + 4 + 5
P = 12 units
The perimeter of the scalene triangle is 12 units.
Quiz
Tips and Tricks
1. Equilateral Triangle
Tip: To find the perimeter of an equilateral triangle, use the formula P = 3s, where s is the length of one side.
2. Isosceles Triangle
Tip: When calculating the perimeter of an isosceles triangle, use the formula P = 2a + b, where a is the length of the equal sides, and b is the length of the unequal side.
3. Scalene Triangle
Tip: For a scalene triangle, the perimeter is found by adding the lengths of all three sides, using the formula P = a + b + c, where a, b, and c are the lengths of the three sides.
4. Perimeter of Triangle
Tip: Remember that the perimeter of a triangle is the sum of the lengths of all three sides, regardless of the type of triangle.
5. Real Life Application of Perimeter of Triangle
Tip: Understanding the perimeter of a triangle is crucial in various real-life scenarios, such as construction, landscaping, and design projects.
Real life application
Story: “The Perimeter Quest of Maya and Ethan”
Maya and Ethan, two young explorers, embarked on a quest to uncover the real-life applications of the perimeter of a triangle. Their journey led them to various challenges that showcased the practical significance of this geometric concept.
Challenge 1: The Garden Planning
Maya and Ethan visited a botanical garden where they encountered a triangular flower bed. The gardener explained that the perimeter of the flower bed determined the length of fencing needed to enclose it. By understanding the perimeter formula for each type of triangle, Maya and Ethan were able to assist the gardener in planning the fencing requirements for the garden.
Challenge 2: The Roof Construction
As they ventured into a construction site, Maya and Ethan observed the installation of a triangular roof. The construction workers emphasized the importance of calculating the perimeter to ensure the accurate placement of roofing materials. Maya and Ethan applied their knowledge of the perimeter formula for isosceles triangles to assist the workers in measuring the required materials.
Challenge 3: The Artistic Endeavor
In an art studio, Maya and Ethan encountered a triangular mural being created by a local artist. The artist explained that understanding the perimeter of the mural was crucial in determining the amount of paint needed to cover the entire surface. By utilizing the perimeter formula for scalene triangles, Maya and Ethan were able to assist the artist in estimating the paint requirements for the mural.
FAQ's
The formula for the perimeter of an equilateral triangle is P = 3s, where P is the perimeter and s is the length of one side.
The perimeter of an isosceles triangle is calculated using the formula P = 2a + b, where P is the perimeter, a is the length of the equal sides, and b is the length of the unequal side.
The perimeter of a scalene triangle is calculated by adding the lengths of all three sides, using the formula P = a + b + c, where P is the perimeter, and a, b, and c are the lengths of the three sides.
Understanding the perimeter of triangle is crucial in real-life applications such as construction, landscaping, design projects, and measurement of boundaries. It helps in determining the total length of fencing, roofing materials, and other resources required for various projects.
Yes, each type of triangle has its own formula for calculating the perimeter. Whether it’s an equilateral, isosceles, or scalene triangle, the perimeter can be determined using the specific formula for each type of triangle.
Like? Share it with your friends
Facebook
Twitter
LinkedIn