Understanding Perpendicular Lines: Definition and Properties
Table of Contents
Introduction
Perpendicular Lines
Perpendicular lines play a crucial role in geometry and spatial relationships. Let’s delve into the concept of perpendicular lines, explore their properties, and uncover their significance in various contexts.
Analogy of Definition
What are Perpendicular lines?
Perpendicular lines are a fundamental concept in geometry, representing lines that intersect at right angles. This intersection forms four right angles, each measuring 90 degrees.
Method
Properties of Perpendicular Lines
Perpendicular lines are lines that intersect each other at a right angle or 90°, forming a square corner where they meet. It’s like the corners of a piece of paper or the edges of a book.
If you imagine drawing two lines that cross each other and create a perfect “L” shape at their intersection, those lines are perpendicular. They stand straight up and down or straight across from each other.
Perpendicular lines are important in geometry because they help define right angles, which are essential for many geometric concepts and constructions.
If two lines EF and GF are perpendicular to one another, then we can write it as EF ⊥ GH. The symvole ‘⊥’ represents that the lines are perpendicular
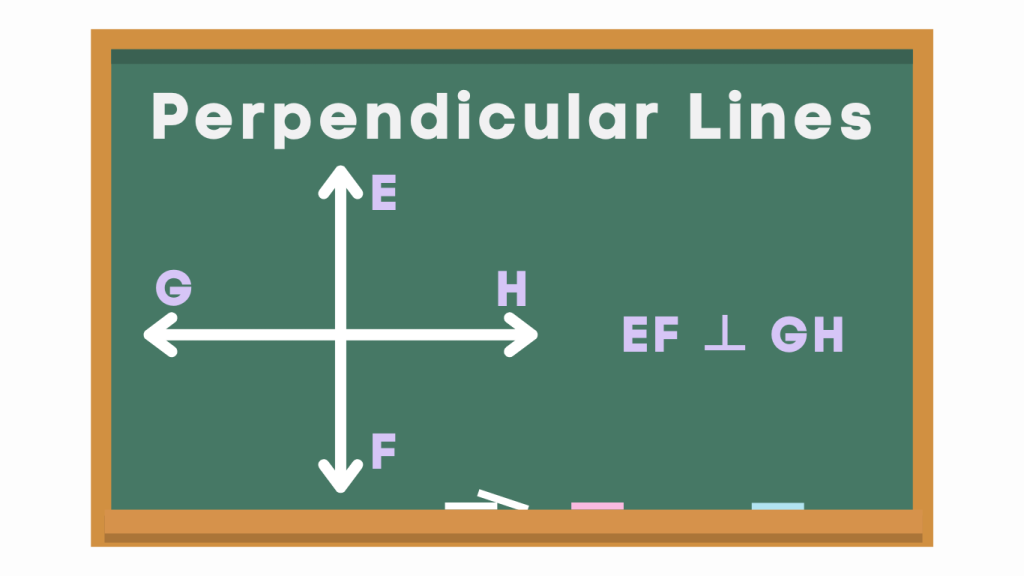
1. Right Angle: Perpendicular lines intersect each other at a right angle, which measures 90 degrees. This means that the angle formed where the lines meet is a right angle.
2. Form Right Triangles: Perpendicular lines create right triangles when extended. The side opposite the right angle (the hypotenuse) is formed by the segment connecting the endpoints of the perpendicular lines.
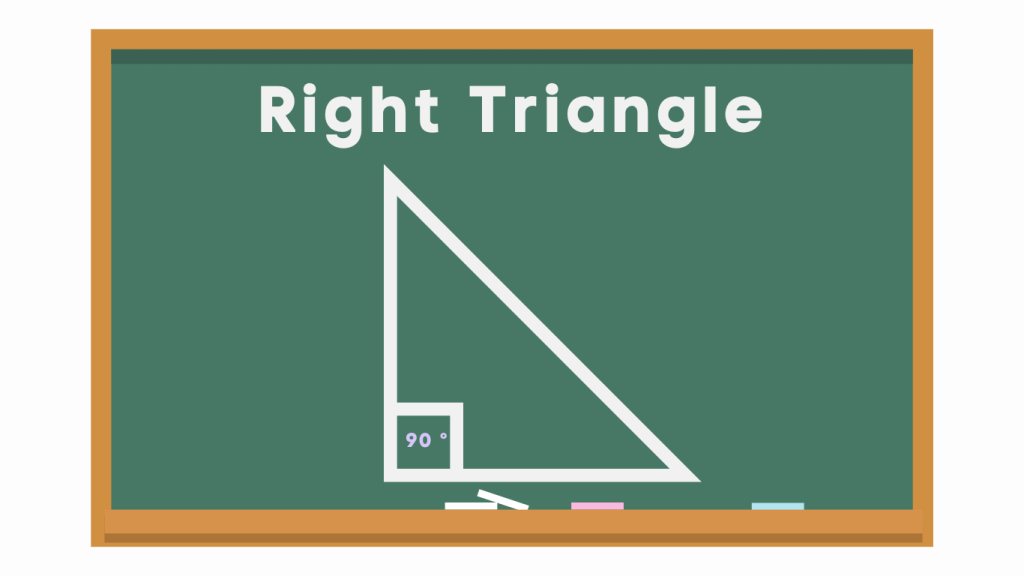
3. Symmetry: Perpendicular lines exhibit symmetry across their point of intersection. This means that if you reflect one line across the intersection point, you will get the other line.
4.Equidistant: Points on one perpendicular line are equidistant from the other perpendicular line. This property is useful for constructing perpendicular bisectors and finding the midpoint of line segments.
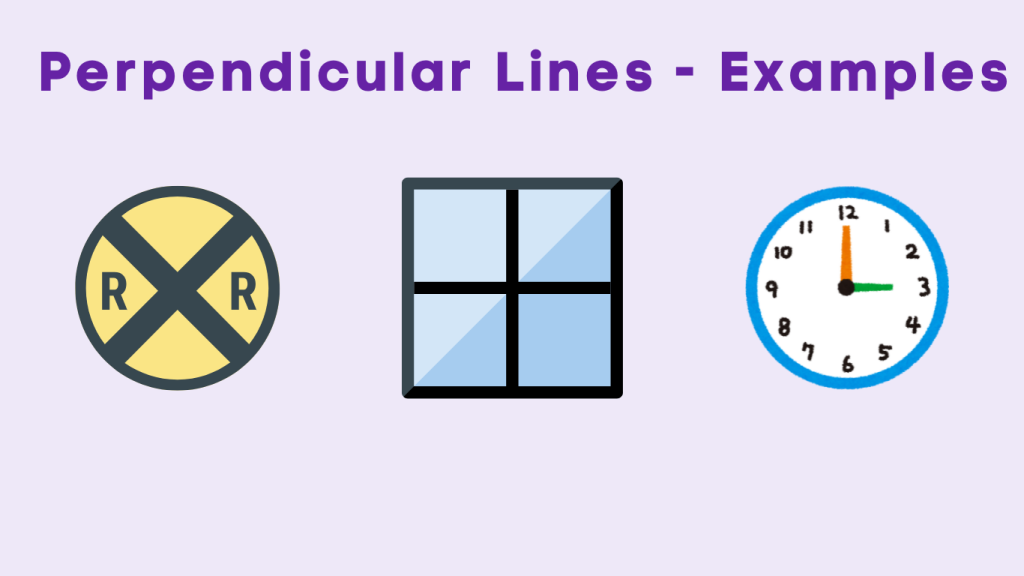
Examples
Summary: This example demonstrates the process of identifying perpendicular lines in a coordinate plane based on the product of their slopes. By calculating the product of the slopes and determining that it equals -1, the perpendicular nature of the lines is established.
Quiz
Tips and Tricks
1. Visualize Right Angles
Tip: When you see two lines intersecting and forming a perfect square corner, you can quickly identify them as perpendicular lines because they create right angles.
2. Use a Protractor
Tip: If you have a protractor handy, you can measure the angles where two lines intersect. If the angle measures exactly 90 degrees, then the lines are perpendicular.
3. Look for Symmetry
Tip: Perpendicular lines exhibit symmetry across their point of intersection. If you reflect one line across the point of intersection and it matches up with the other line, they are perpendicular.
4. Find Right Triangles
Tip: Perpendicular lines create right triangles when extended. If you can identify a right triangle formed by extending the lines, then they are perpendicular.
5. Check Equidistance
Tip: Points on one perpendicular line are equidistant from the other perpendicular line. If you can identify points that are equidistant from both lines, then they are perpendicular.
Real life application
Scenario: Architectural Design
In architectural design, the construction of perpendicular walls and the placement of right-angled corners are essential for structural stability and spatial organization.
Scenario: Urban Planning
In urban planning, the intersection of roads at right angles ensures efficient traffic flow and delineates distinct zones within a city.
FAQ's
Perpendicular lines are two lines that intersect at a 90-degree angle, forming right angles. They are often denoted by the symbol ⊥.
Perpendicular lines intersect at right angles, while parallel lines never intersect and maintain a constant distance from each other.
The properties of perpendicular lines include forming right angles at their point of intersection, having slopes that are negative reciprocals of each other, and exhibiting symmetry about the point of intersection.
In a coordinate plane, perpendicular lines can be identified by their slopes. If the product of the slopes of two lines is -1, they are perpendicular.
Real-life examples of perpendicular lines include the corners of a room, the intersection of roads at right angles, and the construction of perpendicular walls in buildings.
Like? Share it with your friends
Facebook
Twitter
LinkedIn