Understanding Quadrilaterals: Definition, Properties, Types, and Examples
Table of Contents
Introduction
Quadrilaterals
In the realm of geometry, the concept of quadrilaterals holds significant importance. From their definition and properties to their various types and real-life examples, exploring the world of quadrilaterals unveils a multitude of intriguing aspects.
Analogy of Definition
What is a Quadrilateral?
A quadrilateral is a polygon with four sides, four vertices, and four angles. It is a fundamental geometric shape that forms the basis for further exploration into the realm of polygons and their properties.
Method
Properties of Quadrilateral
Understanding the properties of quadrilaterals involves delving into their unique characteristics, including the sum of interior angles, the classification based on sides and angles, and the application of these properties in real-world scenarios.
1. Four Sides and Four Angles
A quadrilateral is a polygon with exactly four sides (edges) and four angles (vertices).
2. Sum of Interior Angles
The sum of the interior angles of a quadrilateral is always 360 degrees. This can be shown by dividing the quadrilateral into two triangles, each of which has interior angles summing to 180 degrees.
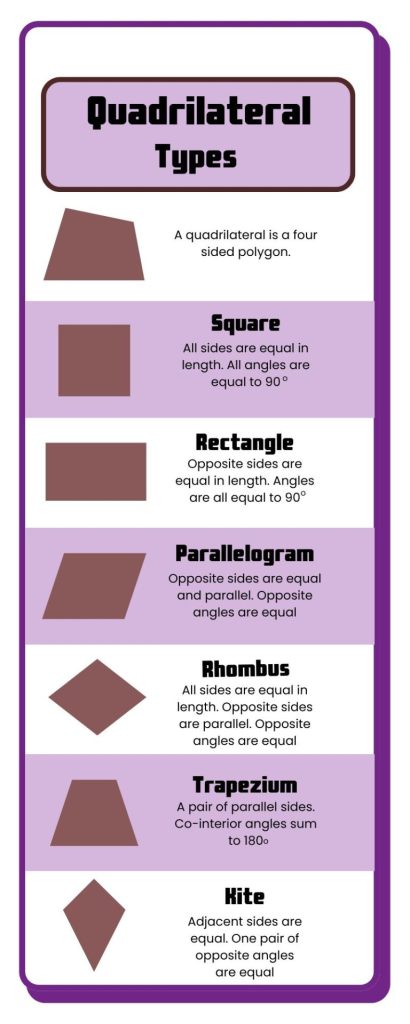
3. Types of Quadrilaterals
There are various specific types of quadrilaterals (such as squares, rectangles, rhombuses, parallelograms, trapezoids, and kites), each with its own unique properties, but all share the general properties listed here.
4. Diagonals
A quadrilateral has two diagonals. The properties of these diagonals (whether they bisect each other, are equal, etc.) depend on the specific type of quadrilateral.
Concave and Convex Quadrilaterals
Convex Quadrilaterals
A convex quadrilateral is a four-sided polygon where all interior angles are less than 180 degrees. In a convex quadrilateral, all vertices point outward, creating a shape that is “bulging” outward. The diagonals of a convex quadrilateral always lie inside the shape. Common examples of convex quadrilaterals include squares, rectangles, and parallelograms. One key property of convex quadrilaterals is that the sum of their interior angles is always 360 degrees. This property, along with the outward-pointing vertices and internal diagonals, helps in distinguishing convex quadrilaterals from other types of four-sided polygons.
Concave Quadrilaterals
A concave quadrilateral, on the other hand, has at least one interior angle greater than 180 degrees, giving it a “caved-in” appearance. This means that one of the vertices points inward, creating a notch or indentation in the shape. In concave quadrilaterals, at least one diagonal will lie outside the polygon. Despite this inward-pointing vertex, the sum of the interior angles in a concave quadrilateral is still 360 degrees. An example of a concave quadrilateral is an arrowhead shape. The distinctive inward angle and the external diagonal are key characteristics that set concave quadrilaterals apart from convex ones.
Types of Quadrilateral
Examples
Summary: This example highlights the fundamental properties of a quadrilateral, emphasizing its four sides, the sum of interior angles, and the diverse classification based on its unique attributes. Understanding these properties is essential for comprehending the nature of quadrilaterals and their significance in geometry.
Quiz
Tips and Tricks
1. Identifying Quadrilateral Type
Tip: Examine the number of sides, vertices, and angles to determine if the shape meets the criteria of a quadrilateral.
2. Calculating Quadrilateral Angles
Tip: Utilize the formula (n-2) * 180 degrees, where n represents the number of sides, to calculate the sum of interior angles.
3. Constructing Quadrilateral Shapes
Tip: Utilize the knowledge of quadrilateral properties and types to construct the desired shape accurately.
Real life application
Scenario: Architectural Design
Architects and designers utilize quadrilateral shapes in creating floor plans, building layouts, and structural frameworks, where the understanding of their properties and types is crucial for ensuring stability and aesthetic appeal.
Scenario: Engineering Blueprints
Engineers employ quadrilaterals in designing bridges, roadways, and infrastructure, where the analysis of their properties and angles is essential for determining structural integrity and load-bearing capacity.
FAQ's
A quadrilateral is a polygon with four sides, four vertices, and four angles. It is a closed figure formed by connecting four line segments.
The properties of a quadrilateral include having four sides, four angles, the sum of interior angles equaling 360 degrees, and the ability to be classified based on its angles and sides.
Quadrilaterals can be classified into various types such as parallelograms, rectangles, squares, rhombuses, trapezoids, and kites, based on their unique properties and characteristics.
Quadrilateral shapes find practical applications in architecture, engineering, design, and construction, where the understanding of their properties and types is essential for creating and analyzing structures and layouts.
The key characteristics of a quadrilateral include having four sides, four vertices, four angles, and the ability to be classified based on its properties and attributes.
Like? Share it with your friends
Facebook
Twitter
LinkedIn
