Subtracting Fractions – Rules and Examples
Table of Contents
Introduction
What is subtracting fractions?
Fractions are an essential part of mathematics, and understanding how to subtract them is a crucial skill. There are different types of fractions such as like fractions, unlike fractions, mixed fractions, and it is essential that we understand the various ways of subtracting. Let’s explore the methods and scenarios for subtracting fractions to master this fundamental mathematical operation.
Analogy of Definition
Subtracting Fractions Explained
Subtracting fractions involves finding the difference between two or more fractions. This process requires careful attention to the denominators and numerators of the fractions to ensure accurate results. Whether the fractions have like denominators, unlike denominators, whole numbers, or mixed fractions, the subtraction process follows specific rules and methods.
Method
Approaches to Subtracting Fractions
There are different approaches to subtracting fractions based on the nature of the fractions involved. When subtracting fractions with like denominators, the process is straightforward. However, when dealing with fractions with unlike denominators, whole numbers, or mixed fractions, additional steps and techniques are required to perform the subtraction accurately.
Subtracting Fractions with Same Denominators
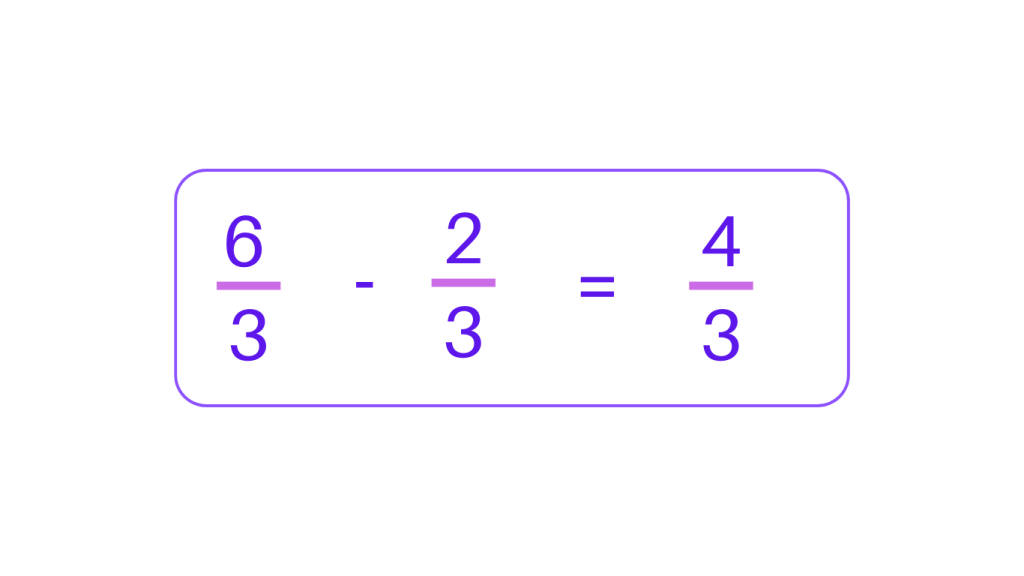
We can simply subtract like fractions by subtracting the numerators of the fraction.
For example, let’s take 6/3 and 2/3. As we just subtract the numerators the solution will be as illustrated below:
Subtracting Fractions with Different Denominators
For subtracting unlike fractions, we will first have to find out the LCM of the denominators so that we can get the same denominators. Then, we can subtract the fractions in a similar manner like fractions with same denominator.
Let’s take an example, \frac{4}{2} and \frac{1}{3}
Step 1: Find out the LCM of the denominators, i.e 2 and 3. The LCM of 2 and 3 is 2 × 3 = 6
Step 2: Make both the denominators same.
\frac{4 × 3}{2 × 3} = \frac{12}{6} and \frac{1 × 2}{3 × 2} = \frac{2}{6}
Step 3: Subtract the numerators of the converted fractions.
\frac{12}{6} – \frac{2}{6} = \frac{10}{6} = \frac{5}{3}
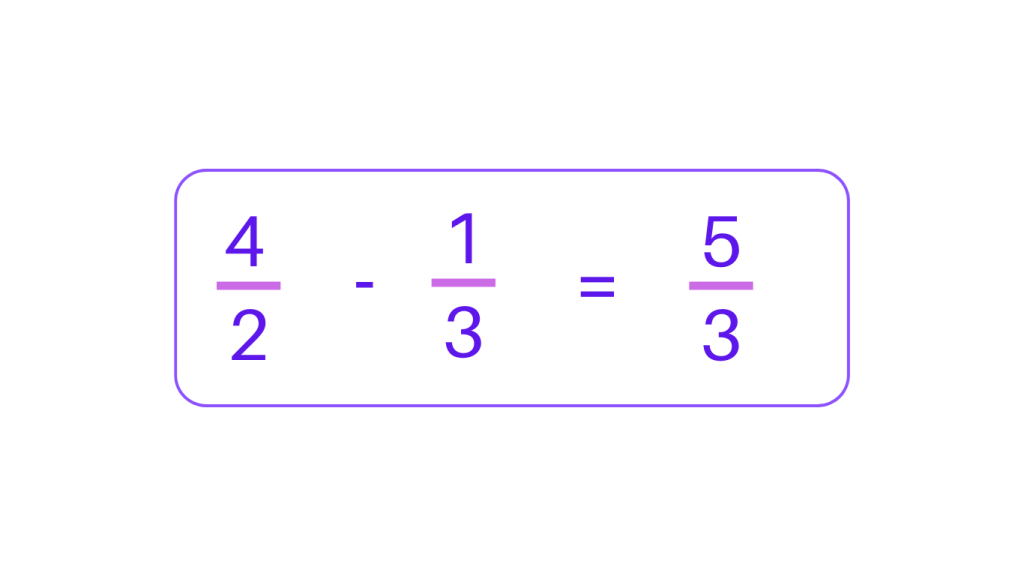
Subtracting Fractions with Whole Numbers
We can subtract fractions with whole numbers by writing the whole numbers in the form of fraction. To write the whole number as fraction, we will put 1 as the denominator. Then, we will subtract the fraction by the applying the same rules as subtracting unlike fractions.
For example: Lets take \frac{5}{2} and 1
Step 1: Convert 1 into a fraction, by putting 1 as the denominator as \frac{1}{1}
Step 2: Subtract \frac{5}{2} and \frac{1}{1}
Step 3: Find out the LCM of 2 and 1, to convert the fractions into like fractions. The LCM is 2
Step 4: Make both the denominators same. \frac{5}{2} and \frac{1 × 2}{1 × 2} = \frac{5}{2} – \frac{2}{2}
Step 5: Subtract \frac{5}{2} – \frac{2}{2}, which will be \frac{3}{2}
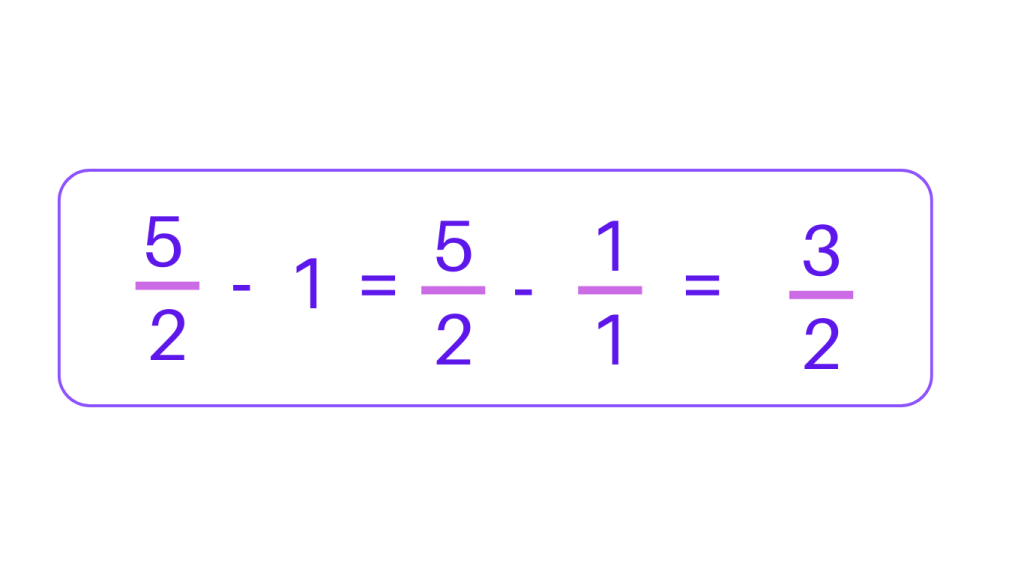
Subtracting fractions is more or less the same as adding fractions, just the process of operation differs a little. To learn more on fractions, visit our site ChimpVine.
Examples
Subtracting Fractions with Like Denominators
Example 1: Subtracting \frac{3}{5} from \frac{4}{5}
Step 1: Since the denominators are the same, subtract the numerators directly.
\frac{4}{5} – \frac{3}{5}
So, the result is\frac{1}{5}
Subtracting Fractions with Unlike Denominators
Example 2: Subtracting 1/3 from 2/5
Step 1: Find the least common multiple (LCM) of the denominators, which is 15.
Step 2: Convert the fractions to equivalent fractions with the common denominator.
2/5 becomes 6/15 and 1/3 becomes 5/15.
Step 3: Subtract the fractions with the common denominator.
6/15 – 5/15 = 1/15
So, the result is 1/15
Subtracting Mixed Fractions
Example 3: Subtracting 2\frac{1}{4}from 3\frac{3}{8}
Step 1: Convert the mixed fractions to improper fractions.
3\frac{3}{8} becomes \frac{27}{8} and 2\frac{1}{4} becomes \frac{9}{4}
Step 2: Find a common denominator, which is 8.
Step 3: Subtract the fractions with the common denominator.
\frac{27}{8} – \frac{9}{4} = \frac{27}{8} – \frac{18}{8}= \frac{9}{8}
So, the result is \frac{9}{8}
Quiz
Tips and Tricks
1. Subtracting Fractions with Like Denominators
Tip: When subtracting fractions with same denominators, simply subtract the numerators and keep the denominator unchanged.
Calculation: 4/5 – 3/5 = 1/5
2. Subtracting Fractions with Unlike Denominators
Tip: Find the least common multiple (LCM) of the denominators and convert the fractions to equivalent fractions with the common denominator before subtracting.
Calculation: 2/5 – 1/3 = 6/15 – 5/15 = 1/15
3. Subtracting Mixed Fractions
Tip: Convert the mixed fractions to improper fractions, find a common denominator, and then subtract the fractions.
Calculation: 3\frac{5}{2} – 1\frac{1}{2} = \frac{11}{2} – \frac{3}{2}= \frac{8}{2} = 4
4. Subtracting Fraction with Whole Numbers
Tip: Convert the whole number to a fraction with the same denominator as the other fraction before performing the subtraction.
Calculation: 5 – 2 1/3 = 15/3 – 7/3 = 8/3
5. Simplifying the Result
Tip: After subtracting the fractions, simplify the result if possible to express it in its simplest form.
Calculation: 9/3 can be simplified to 3
Real life application
Story: How Subtracting Fractions Helped Ethan and Maya
Maya and Ethan, two young math enthusiasts, embarked on a series of adventures that required them to apply their knowledge of subtracting fractions in real-life scenarios.
Challenge 1: The Pizza Party Planning
Maya and Ethan were planning a pizza party and needed to calculate how much pizza would be left after serving a certain number of slices. By subtracting the consumed slices from the total, they determined the remaining pizza accurately.
Challenge 2: The Baking Experiment
In their baking experiment, Maya and Ethan had to adjust the recipe by subtracting a portion of the ingredients to achieve the desired flavor and texture. Their understanding of subtracting fractions helped them modify the recipe effectively.
Challenge 3: The Art of Sharing
When sharing toys and treats with their friends, Maya and Ethan used fraction subtraction to ensure fair distribution and determine the remaining items after sharing.
FAQ's
When subtracting fractions with like denominators, simply subtract the numerators and keep the denominator unchanged to find the result.
To subtract fractions with unlike denominators, find the least common multiple (LCM) of the denominators, convert the fractions to equivalent fractions with the common denominator, and then subtract the fractions.
Yes, you can subtract whole numbers from fractions by converting the whole number to a fraction with the same denominator as the other fraction before performing the subtraction.
To subtract mixed fractions, convert the mixed fractions to improper fractions, find a common denominator, and then subtract the fractions to obtain the result.
It is recommended to simplify the result after subtracting fractions to express it in its simplest form, especially when dealing with mixed fractions or improper fractions.
Like? Share it with your friends
Facebook
Twitter
LinkedIn