Understanding the Different Types of Fractions
Table of Contents
Introduction
Fractions
Fractions are a fundamental concept in mathematics, representing a portion of a whole or a group of objects. They are expressed as a numerator over a denominator, where the numerator signifies the number of parts being considered, and the denominator indicates the total number of equal parts or objects in the whole.
For instance, imagine a pizza sliced into eight equal pieces. Each slice, or part of the pizza, represents \frac{1}{8} of the whole. Here, the numerator is 1, indicating one slice, and the denominator is 8, representing the total number of slices in the pizza. So, \frac{1}{8} reads as “one eighth.”
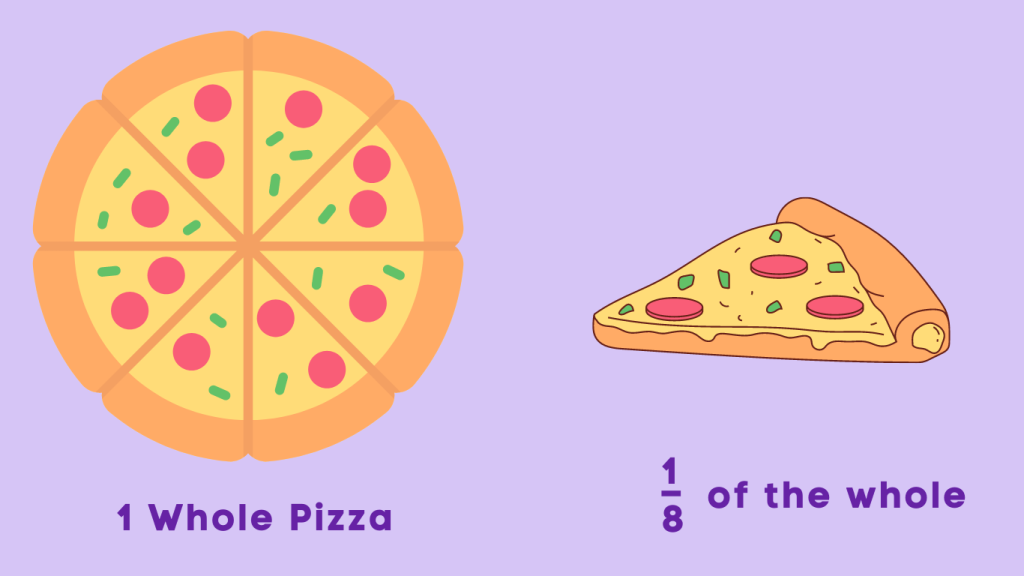
Understanding fractions is crucial for various mathematical operations, such as addition, subtraction, multiplication, and division. They allow us to represent and work with parts of a whole in a precise and systematic manner, making them indispensable in many real-world applications and problem-solving scenarios.
In this article, we will explore the various types of fractions and understand their unique characteristics.
Analogy of Definition
Types of Fractions
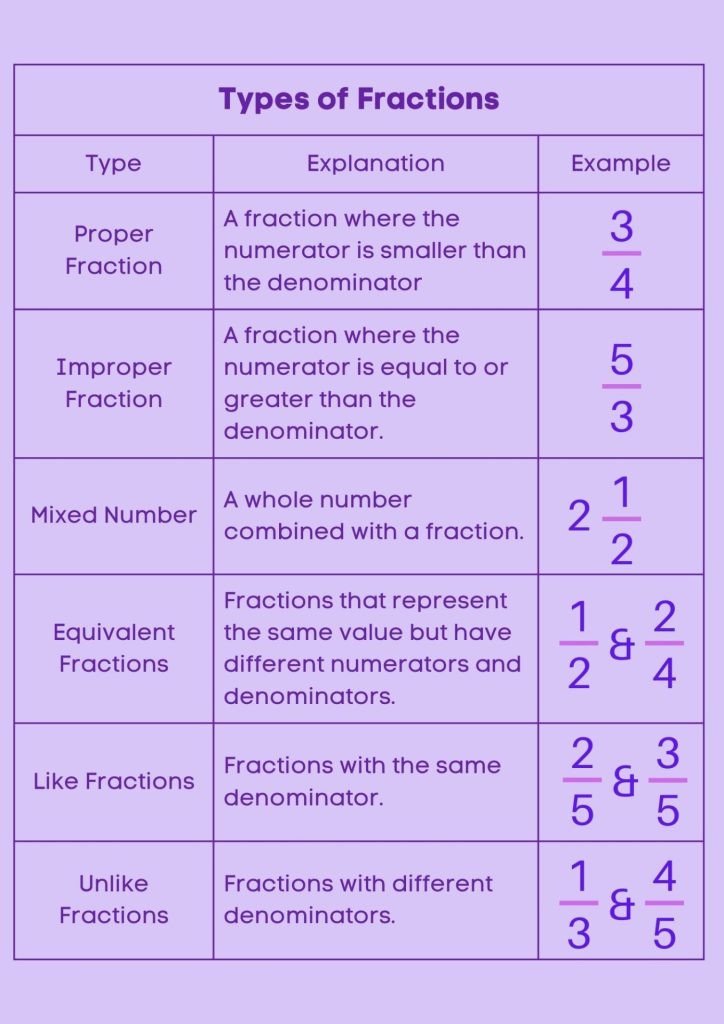
Fractions can be classified into different types based on their properties and structure. The main types of fractions include proper fractions, improper fractions, mixed fractions, like fractions, unlike fractions, and equivalent fractions.
Method
Proper Fraction
A proper fraction is a fraction in which the numerator (the top number) is less than the denominator (the bottom number). In other words, the value of the fraction is less than 1. For example, \frac{3}{4} and \frac{5}{8} are proper fractions.
Improper Fraction
An improper fraction is a fraction in which the numerator is greater than or equal to the denominator. This means that the value of the fraction is equal to or greater than 1. For example, \frac{7}{4} and \frac{11}{3} are improper fractions.
Mixed Fraction
A mixed fraction is a combination of a whole number and a proper fraction. It is written in the form of a whole number followed by a proper fraction. For example, 2\tfrac{1}{3} and 5\tfrac{2}{5}are mixed fractions.
Like Fractions
Like fractions are fractions that have the same denominator. When adding or subtracting like fractions, you simply add or subtract the numerators while keeping the common denominator unchanged. For example, \frac{1}{4} and \frac{3}{4} are like fractions.
Unlike Fractions
Unlike fractions are fractions that have different denominators. When adding or subtracting unlike fractions, you need to find a common denominator before performing the operation. For example, \frac{1}{3} and \frac{2}{5} are unlike fractions.
Equivalent Fractions
Equivalent fractions are fractions that represent the same value, even though they may look different. They have different numerators and denominators, but when simplified, they are equal. For example, \frac{1}{2} ,\frac{2}{4} , and \frac{3}{6} are equivalent fractions.
Examples
1. Proper Fraction: \frac{3}{5}
2. Improper Fraction: \frac{7}{2}
3. Mixed Fraction: 4\tfrac{1}{2}
4. Like Fractions: \frac{2}{3} and \frac{4}{3}
5. Unlike Fractions: \frac{1}{4} and \frac{3}{5}
6. Equivalent Fractions: \frac{2}{4} and \frac{3}{6}
Quiz
Tips and Tricks
1. Proper Fraction
Tip: A proper fraction has a numerator that is less than the denominator, representing a value less than 1.
2. Improper Fraction
Tip: An improper fraction has a numerator that is greater than or equal to the denominator, representing a value equal to or greater than 1.
3. Mixed Fraction
Tip: A mixed fraction is a combination of a whole number and a proper fraction, written in the form of a whole number followed by a proper fraction.
4. Like Fractions
Tip: Like fractions have the same denominator, making it easier to add or subtract them without changing the denominator.
5. Unlike Fractions
Tip: Unlike fractions have different denominators, requiring the determination of a common denominator before performing addition or subtraction.
Real life application
Scenario: “Sharing Pizza Slices”
When dividing a pizza among friends, you may encounter different types of fractions. Proper fractions represent the individual slices each person receives, while mixed fractions can be used to represent the total number of whole pizzas and remaining slices.
Scenario: “Baking Recipes”
Baking recipes often require measurements in fractions, such as 1/2 cup of flour or 3 1/4 teaspoons of sugar. Understanding the different types of fractions is essential for accurate measurements and successful baking.
Scenario: “Construction Projects”
In construction projects, measurements and dimensions are often expressed in fractions. Proper and improper fractions are used to represent lengths, widths, and heights, ensuring precise and detailed construction plans.
Scenario: “Financial Calculations”
Financial calculations, such as interest rates and loan payments, may involve working with fractions. Understanding equivalent fractions is important for comparing different financial terms and making informed decisions.
Scenario: “Art and Design”
In art and design, fractions are used to determine proportions, measurements, and dimensions of various elements. Like and unlike fractions are utilized to ensure accurate and harmonious compositions in artistic creations.
FAQ's
The main difference between a proper fraction and an improper fraction lies in the relationship between the numerator and the denominator. In a proper fraction, the numerator is less than the denominator, while in an improper fraction, the numerator is greater than or equal to the denominator.
Mixed fractions are different from proper and improper fractions in that they consist of a whole number and a proper fraction combined. They are written in the form of a whole number followed by a proper fraction, representing a value greater than 1.
Like fractions have the same denominator, making it easier to add or subtract them without changing the denominator. Unlike fractions have different denominators, requiring the determination of a common denominator before performing addition or subtraction.
Understanding equivalent fractions is important as it allows us to represent the same value in different ways. It helps in simplifying fractions, comparing quantities, and performing operations with fractions more efficiently.
Fractions have practical applications in various real-life scenarios, such as sharing food, measuring ingredients, calculating dimensions, managing finances, and creating artistic compositions. They are essential for accurate representation and communication of quantities and proportions in everyday life.
Like? Share it with your friends
Facebook
Twitter
LinkedIn