Angles – Meaning, Types, Measurement and Examples
Table of Contents
Introduction
Angles
Angles are fundamental elements in mathematics that play a crucial role in various geometric and trigonometric concepts. Understanding the concept of angles is essential for solving problems related to shapes, lines, and measurements. Let’s dive into the world of angles and explore their properties and applications.
Analogy of Definition
What is an Angle?
In geometry, an angle is formed by two rays or line segments that share a common endpoint, known as the vertex. The two rays are referred to as the sides of the angle. Angles are typically measured in degrees and are used to describe the amount of rotation between the two sides.
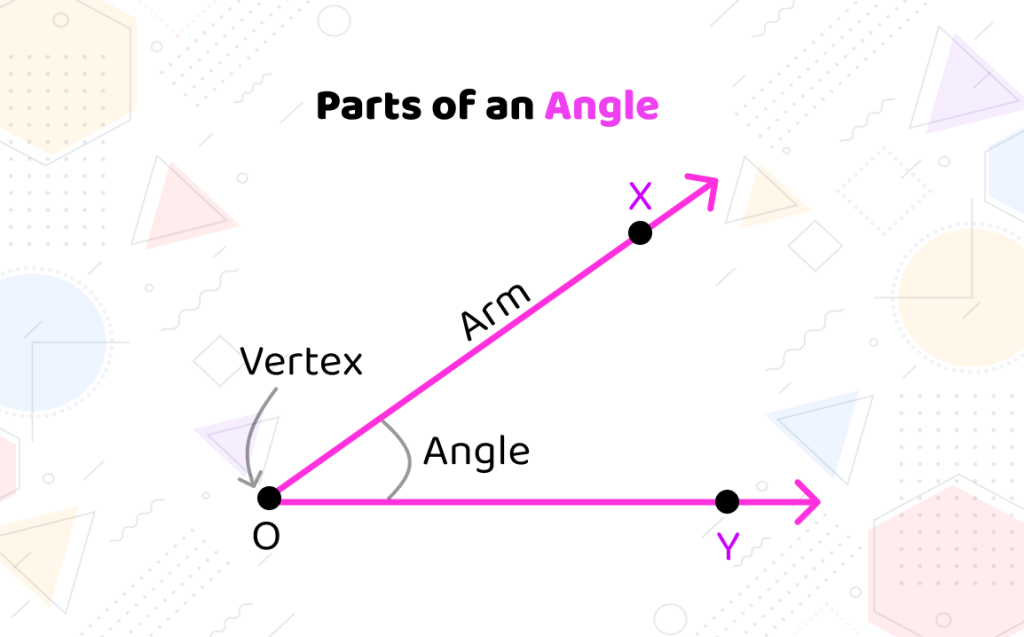
Parts of an Angle
An angle consists of several components, including the vertex, arms, and interior. The vertex is the common endpoint of the two rays, while the rays themselves are known as the arms of the angle. The space between the arms, known as the interior of the angle, determines the angle’s measurement.
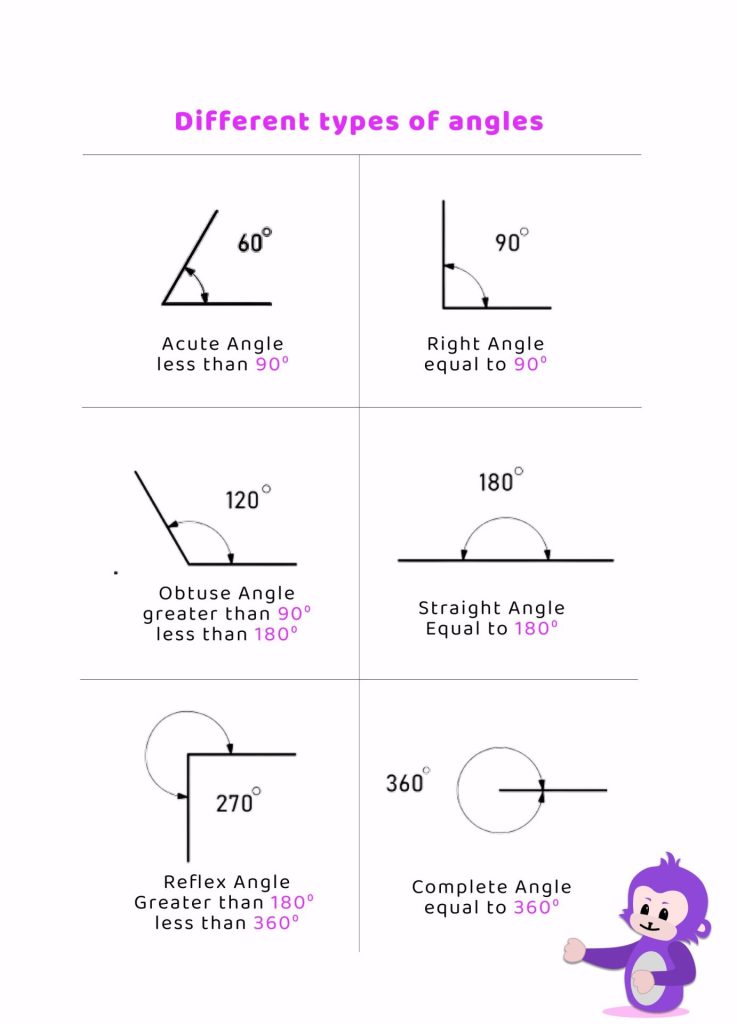
Types of Angles
There are several types of angles based on their measurements and characteristics. These include:
1. Acute Angle: An angle that measures less than 90 degrees.
2. Obtuse Angle: An angle that measures more than 90 degrees but less than 180 degrees.
3. Right Angle: An angle that measures exactly 90 degrees.
4. Straight Angle: An angle that measures exactly 180 degrees, forming a straight line.
5. Reflex Angle: An angle that measures more than 180 degrees but less than 360 degrees.
6. Complete Angle: An angle that measures exactly 360 degrees, forming a complete circle.
Interior and Exterior Angles
In geometric figures such as polygons, the interior angles are the angles formed inside the shape, while the exterior angles are formed outside the shape. The sum of the interior angles of a polygon depends on the number of sides, while the sum of the exterior angles is always 360 degrees.
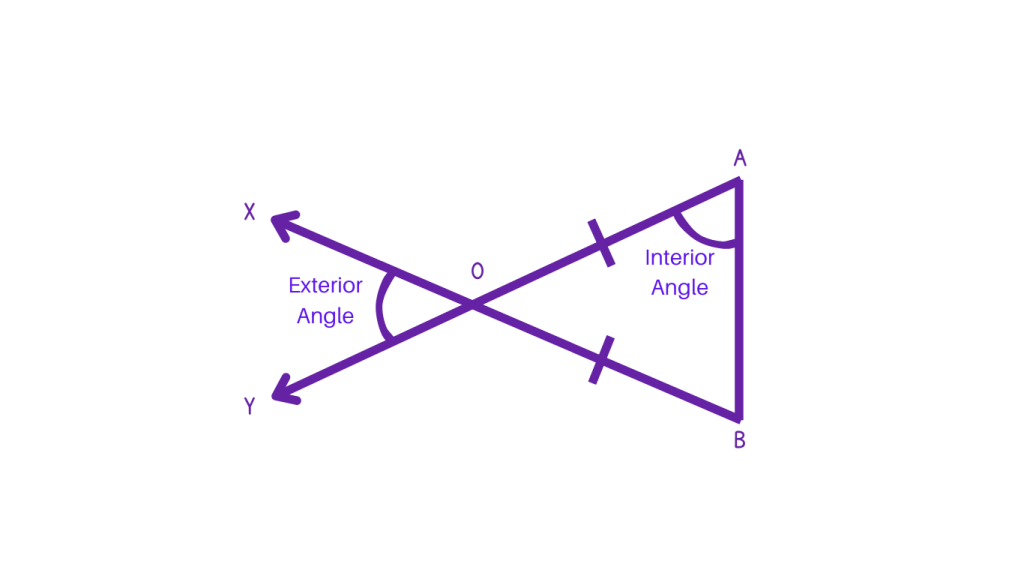
In the given figure, ∠OAB, ∠OBA and ∠AOB, are interior angles while ∠XOY is exterior angle.
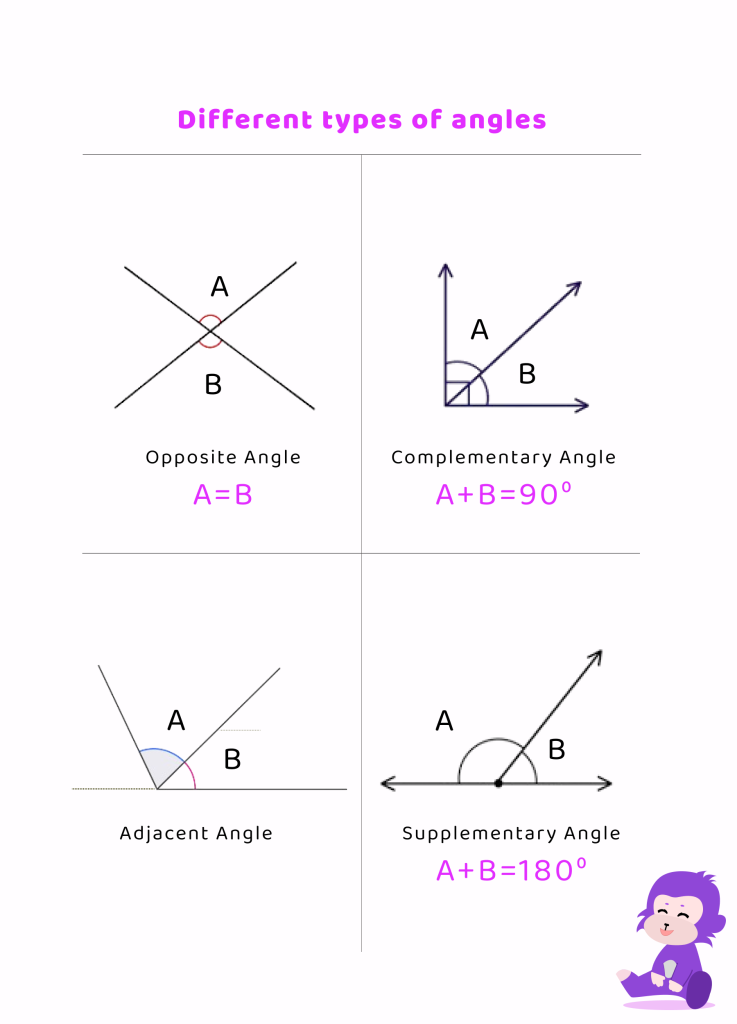
Complementary and Supplementary Angles
Complementary angles are two angles that add up to 90 degrees, while supplementary angles are two angles that add up to 180 degrees. Understanding these relationships is essential for solving problems involving angle measurements and calculations.
Find more fun activites related to angles on our site, ChimpVine.
Method
How to Draw and Measure Angles
Drawing and measuring angles can be done using various tools such as a protractor or a compass. To draw an angle, you can use a protractor to measure the desired angle and then use a ruler to draw the lines accordingly. Measuring angles involves aligning the protractor with the vertex and reading the measurement from the scale.
Steps to Measure Angles
Step 1: Place the center of the protractor on the vertex of the angle and align the bottom of the protractor with the ray.
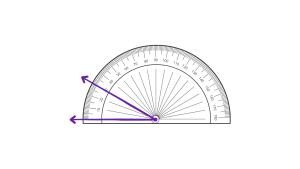
Step 2: Read where the second arm of the angle intersects the protractor.
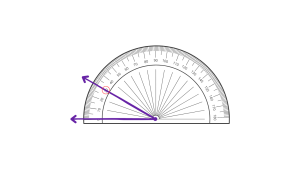
The angle is 30° .
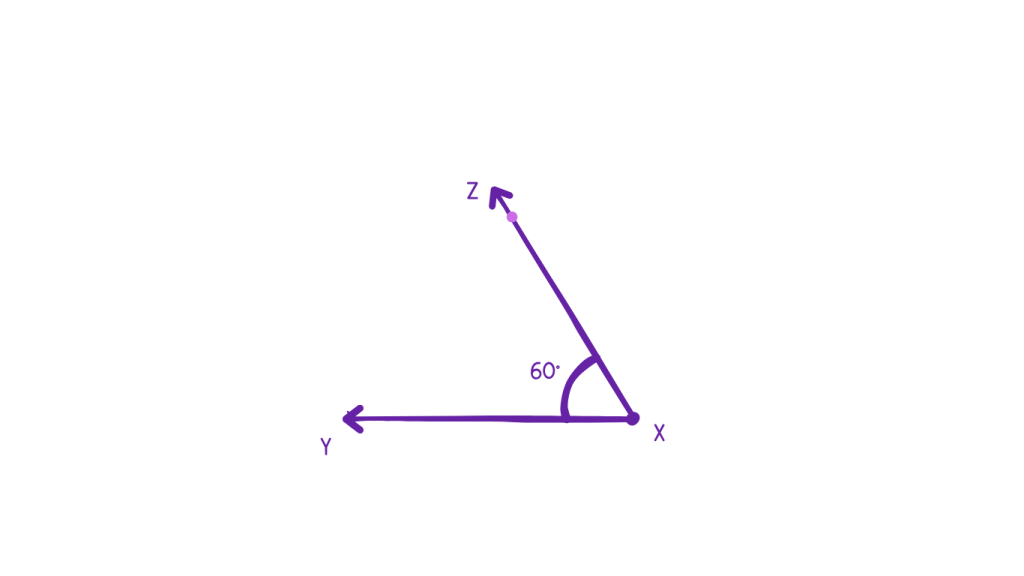
Steps to Draw an Angle
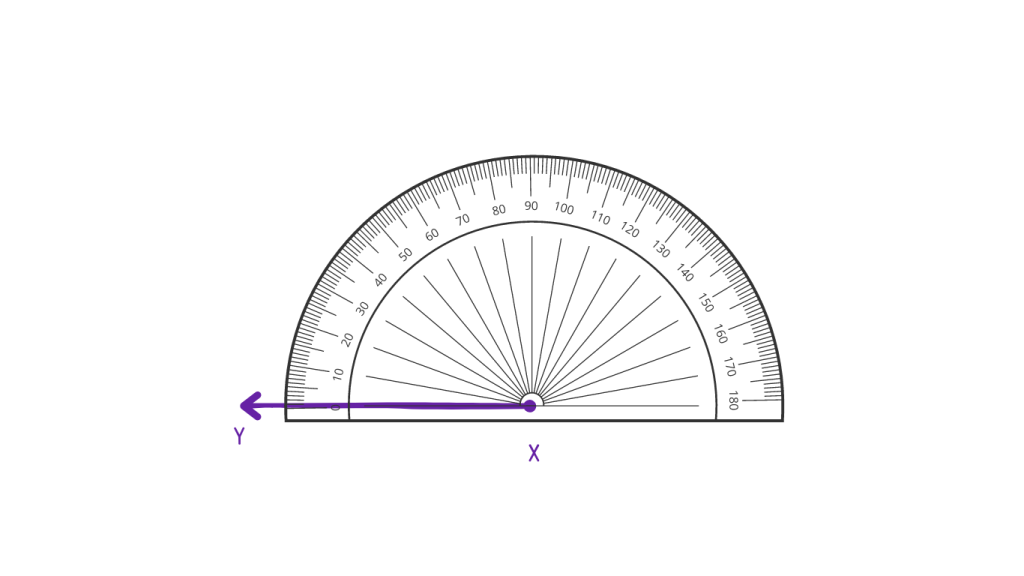
Step 1: Draw a ray and place the center of the protractor on one point of the ray like so.
Step 2: To make an angle of 60°, find 60 on te protractor and mark a point named Z above it.
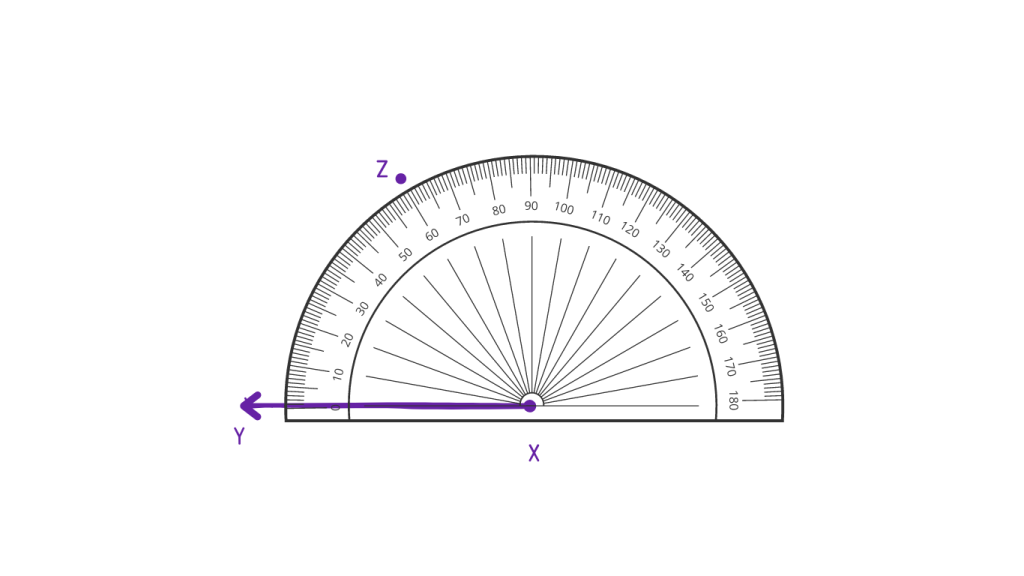
Step 3: Remove the protractor and draw a line beginning at X using a ruler. Hence, ∠XYZ = 60° .
Examples
Identifying Angle Types
Example 1: Identify the type of angle formed by the hands of a clock at 3:00.
Answer: Right Angle (90°)
Example 2: Identify the type of angle formed by the hands of a clock at 6:00.
Answer: Straight Angle (180°)
Quiz
Tips and Tricks
1. Angle Identification Tip
Tip: Remember that a right angle measures 90 degrees, a straight angle measures 180 degrees, and an acute angle measures less than 90 degrees.
2. Interior and Exterior Angle Calculation
Tip: For a polygon with n sides, the sum of the interior angles can be calculated using the formula (n-2) * 180 degrees.
3. Complementary and Supplementary Angle Identification
Tip: Complementary angles add up to 90 degrees, while supplementary angles add up to 180 degrees. Look for angle pairs that satisfy these conditions.
4. Drawing and Measuring Angles Technique
Tip: Place the center of the protractor on the vertex of the angle, align one arm with the 0-degree mark, and read the measurement from the scale.
5. Angle Properties Understanding
Tip: The Triangle Sum Property states that the sum of the interior angles of a triangle is always 180 degrees, regardless of the triangle’s size or shape.
Real life application
Story: “The Angle Adventures of Maya and Ethan”
Maya and Ethan, two curious students, embarked on a series of adventures that required them to apply their knowledge of angles to solve real-life challenges.
Challenge 1: The Architect’s Blueprint
Maya and Ethan visited an architect’s office, where they were tasked with analyzing the blueprints of a new building. They had to identify the types of angles formed by the intersecting lines and determine the measurements of the interior angles of the rooms. By understanding the properties of angles, they were able to assist the architect in creating accurate designs.
Challenge 2: The Geocaching Quest
As part of a geocaching adventure, Maya and Ethan encountered a series of clues that required them to calculate the exterior angles of various geometric shapes hidden in the park. By applying their knowledge of angle properties, they were able to decipher the clues and locate the hidden treasures.
Challenge 3: The Surveyor’s Mission
In their final challenge, Maya and Ethan joined a team of surveyors to map out a new hiking trail. They had to measure the angles of the trail’s turns and calculate the complementary and supplementary angles to ensure the trail’s safety and accessibility. Their understanding of angle relationships proved to be invaluable in completing the surveying mission.
FAQ's
The different types of angles include acute, obtuse, right, straight, reflex, and complete angles. Each type has specific characteristics based on its measurement and relationship with other angles.
Interior angles are the angles formed inside a geometric figure, such as a polygon, while exterior angles are formed outside the figure. The sum of the interior angles depends on the number of sides, while the sum of the exterior angles is always 360 degrees.
Complementary angles add up to 90 degrees, while supplementary angles add up to 180 degrees. Understanding these angle relationships is important for solving problems involving angle measurements and calculations.
Drawing and measuring angles can be done using tools such as a protractor or a compass. To draw an angle, you can use a protractor to measure the desired angle and then use a ruler to draw the lines accordingly. Measuring angles involves aligning the protractor with the vertex and reading the measurement from the scale.
Angles have practical applications in various professions such as architecture, engineering, surveying, and design. They are used to create accurate blueprints, map out structures, and solve spatial problems in real-world scenarios.
Like? Share it with your friends
Facebook
Twitter
LinkedIn