Number Properties – Definition, Types and Examples
Table of Contents
Introduction
Exploring Number Properties
Number properties play a crucial role in understanding the behavior of numbers and their operations. From the associative and commutative properties to the distributive and identity properties, each concept offers valuable insights into the relationships between numbers and their operations.
Analogy of Definition
What are Number Properties?
Number properties are the rules that govern the behavior of numbers and their operations. These properties include the associative property, commutative property, distributive property, and identity property, each of which provides fundamental principles for performing mathematical operations such as addition and multiplication.
Method
Understanding the Number Properties
To comprehend the various number properties, it is essential to explore each concept in detail and understand how they influence mathematical operations. By examining the properties through examples and applications, one can gain a deeper understanding of their significance in mathematics.
Commutative Property
The commutative property asserts that the order in which numbers are added or multiplied does not change the result. As per this number property, moving the order of a number in either addition or multiplication, doesn’t change the result.
In addition, this means that changing the order of the addends does not affect the sum, and for multiplication, changing the order of the factors does not alter the product.
Commutative Property of Addition
According to the commutative property of addition, while adding two numbers, the order of the addends does not affect the sum
Let us take two numbers, 3 and 5.
To add those numbers, we can write it as 3 + 5
or, we can also write its as 5 + 3
In both the cases we get the same answers, or in other words,
3 + 5 = 5 + 3 = 8
Commutative Property of Multiplication
When two numbers are mutiplied, the order in which we multiply doesn’t have any impact on the answer.
For example: The product of 2 and 5 is 10. Similarly, the product of 5 and 2 is also 10.
Hence, 2 × 5 = 5 × 2 = 10
Associative Property
The associative property states that the way in which numbers are grouped or associated in an addition or multiplication expression does not affect the result.
Associative Property in Addition
When adding three or more numbers, the grouping of the numbers can be changed without altering the sum.
For example: We can group the numbers 4, 7, and 2 as either (4 + 7) + 2 or 4 + (7 + 2). In both the ways, we get the same sum, i.e. 13.
Associative Property in Multiplication
When multiplying three or more numbers, the grouping of the numbers can be changed without affecting the product.
For example: We can group the numbers 3, 2, and 6 as either (3 × 2 ) × 6 or 3 × (2 × 6). In both the ways, we get the same product, i.e. 36.
Distributive Property
The distributive property describes the relationship between addition and multiplication. It states that when a number is multiplied by the sum of two other numbers, the result is the same as if the number were multiplied by each of the two numbers separately, and then the products were added together. The multiplication distributes over addition.
For example: We can take the numbers 7, 2 and 5
According to the number property, 7 × ( 2 + 5 ) = (7 × 2) + ( 7 × 5) = 49
Identity Property
The identity property refers to the existence of an element in a set that, when combined with another element using a specific operation, leaves the other element unchanged.
Identity Property of Addition
In addition, when we add 0 to any number, the number remains unchanged, or we get the same number as the sum. 0 is called additive identity.
Let’s add 6 to 0, we get 6 + 0 = 6
Identity Property of Multiplication
In case of multiplication, if we multiply 1 to any number, the product will be the same number. Thus, we call 1 a multiplicative identity.
Let’s multiply 4 and 1, we get 4 × 1 = 4
We can understand number properties better with a chart. Let’s assume a, b and c are three numbers.
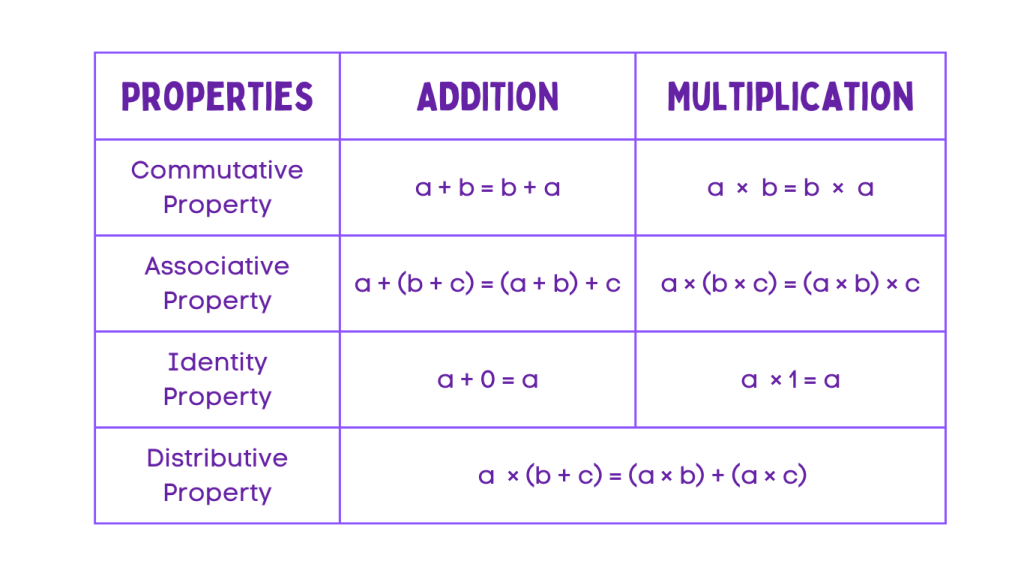
If you want to learn more about number properties, do visit our site Chimpvine.
Examples
Illustrating Number Properties
Example 1: Associative Property
Addition: (2 + 3) + 4 = 2 + (3 + 4) = 9
Multiplication: (2 × 3) × 4 = 2 × (3 × 4) = 24
Example 2: Commutative Property
Addition: 2 + 3 = 3 + 2 = 5
Multiplication: 2 × 3 = 3 × 2 = 6
Example 3: Distributive Property
5 × (6 + 3) = (5 × 6) + (5 × 3) = 45
Example 4: Identity Property
Addition: 5 + 0 = 5
Multiplication: 6 × 1 = 6
Quiz
Tips and Tricks
1. The Associative Property
Tip: When using the associative property, remember that the grouping of numbers can be changed without affecting the result.
Calculation: (2 + 3) + 4 = 2 + (3 + 4) = 9
2. The Commutative Property
Tip: When applying the commutative property, remember that the order of numbers can be changed without altering the result.
Calculation: 7 + 8 = 8 + 7 = 15
3. The Distributive Property
Tip: When using the distributive property, remember that a number multiplied by the sum of two other numbers is equal to the sum of the products of the number with each of the two numbers separately.
Calculation: 3 × (6 + 2) = (3 × 6) + (3 × 2) = 24
4. The Identity Property
Tip: When using the identity property, remember that the identity element for addition is 0, and for multiplication is 1.
Calculation: 9 + 0 = 9
Real life application
Story: “The Number Properties Adventure of Maya and Ethan”
Maya and Ethan, two young mathematicians, embarked on an adventure to explore the real-life applications of number properties. As they encountered various challenges, they discovered how number properties played a crucial role in solving everyday problems.
Challenge 1: The Group Project
Maya and Ethan were assigned a group project that required them to calculate the total cost of purchasing multiple items. By applying the distributive property, they were able to simplify the process by distributing the cost of each item and then adding the products together, saving time and effort.
Challenge 2: The Game of Numbers
In a friendly game of numbers, Maya and Ethan utilized the commutative property to rearrange the order of their moves without changing the outcome. This allowed them to strategize and adapt their gameplay based on the changing sequence of moves, showcasing the practicality of the commutative property.
Challenge 3: The Puzzle of Patterns
As they explored the concept of patterns in nature, Maya and Ethan observed the repetitive nature of certain phenomena. By recognizing the associative property in action, they were able to group and analyze patterns in a more organized and efficient manner, enhancing their understanding of natural phenomena.
FAQ's
The associative property is significant in mathematics as it allows for the grouping of numbers in addition and multiplication expressions without affecting the result. This property simplifies calculations and provides flexibility in performing operations.
The commutative property influences mathematical operations by allowing the order of numbers to be changed in addition and multiplication without altering the result. This property offers versatility in performing calculations and analyzing numerical relationships.
The distributive property is applicable to real-life scenarios, particularly in situations involving the distribution of resources, costs, or quantities. By simplifying the process of distributing and combining values, the distributive property streamlines calculations and problem-solving.
The identity property serves as a foundational element in mathematical operations by providing a neutral element for addition and multiplication. It ensures that the result of an operation remains unchanged when combined with the identity element, contributing to the consistency of mathematical processes.
Number properties contribute to problem-solving and critical thinking by offering fundamental principles for analyzing and manipulating numerical relationships. By understanding and applying number properties, individuals can approach mathematical challenges with enhanced efficiency and adaptability.
Like? Share it with your friends
Facebook
Twitter
LinkedIn