What is a fraction? – Definition, Types & Examples
Table of Contents
Introduction
What is a Fraction?
Fractions are an essential part of mathematics and are used to represent parts of a whole. Understanding fractions is crucial in various mathematical operations and real-life scenarios. Let’s explore the world of fractions and delve into their significance in solving problems.
Analogy of Definition
The Basics of Fractions
A fraction represents a part of a whole or a collection. It consists of two numbers separated by a line, where the number above the line is called the numerator, and the number below the line is called the denominator.
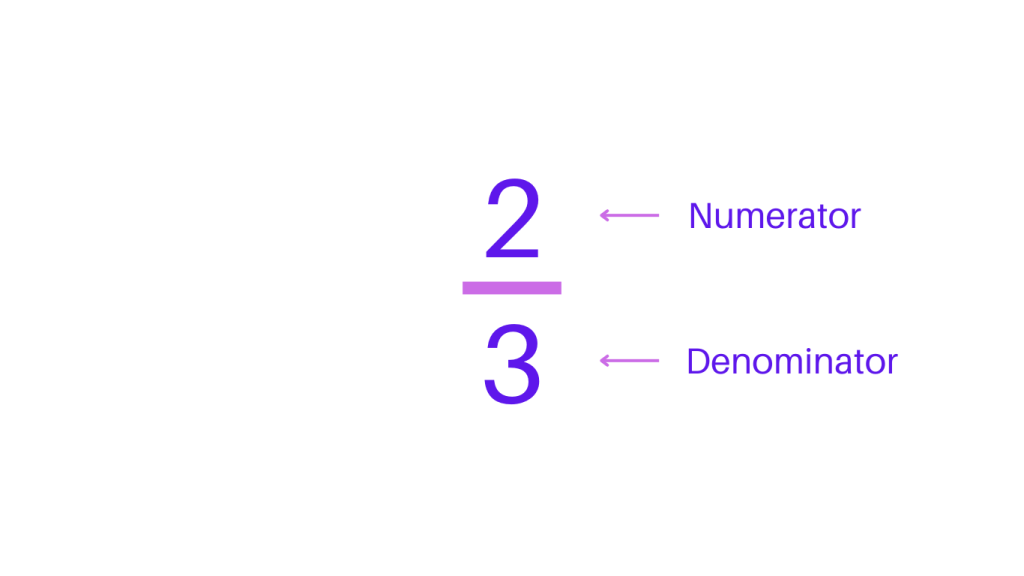The numerator indicates the number of parts being considered, while the denominator represents the total number of equal parts that make up a whole.
Types of Fractions
1. Proper Fraction: A proper fraction is a fraction where the numerator is less than the denominator. For example, 3/4, 2/5, and 5/8 are proper fractions.
2. Improper Fraction:An improper fraction is a fraction where the numerator is greater than or equal to the denominator. For example, 7/4, 9/5, and 11/8 are improper fractions.
3. Mixed Number: A mixed number is a combination of a whole number and a proper fraction. For example, 2\frac{1}{3}, 3\frac{2}{5}, and 4\frac{3}{8} are mixed numbers.
4. Unit Fraction: A unit fraction is a fraction where the numerator is 1. For example, 1/2, 1/3, and 1/4 are unit fractions.
5. Equivalent Fraction: Equivalent fractions are different fractions that represent the same value after reduction. For example, 1/2, 2/4, and 3/6 are equivalent fractions.
Method
Representing Fractions
Fractions can be represented in various ways, including on a number line, in decimal form, and as part of a whole. Understanding these representations is essential in comprehending the concept of fractions and their applications in different contexts.
Fraction as a part of whole
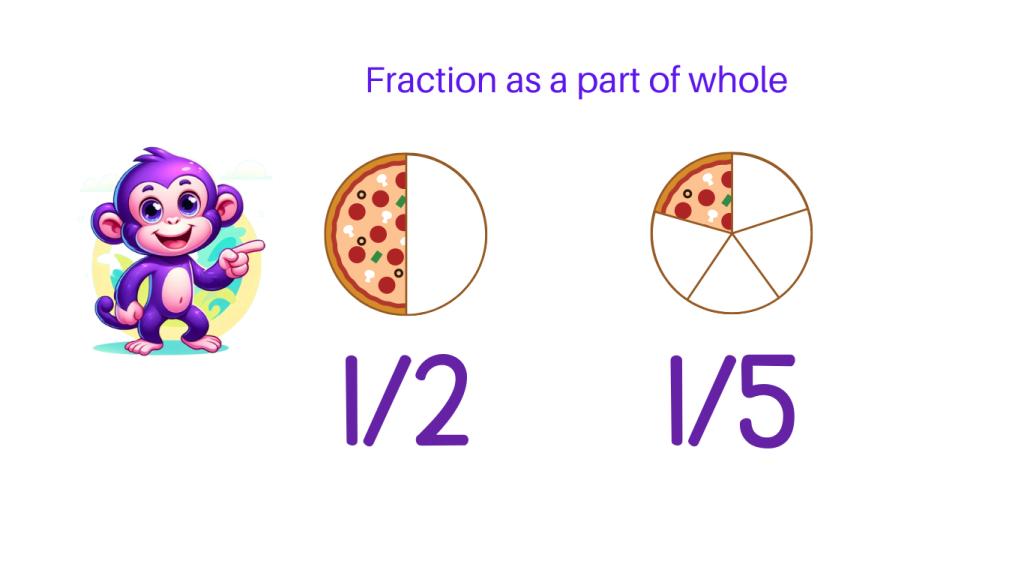
Fractions are generally represented as numerator on top of the denominator. The fraction 1/2 represents 1 part when a whole is divided into 2. Similarly, 1/5 represents 1 part when the whole is divided by 5.
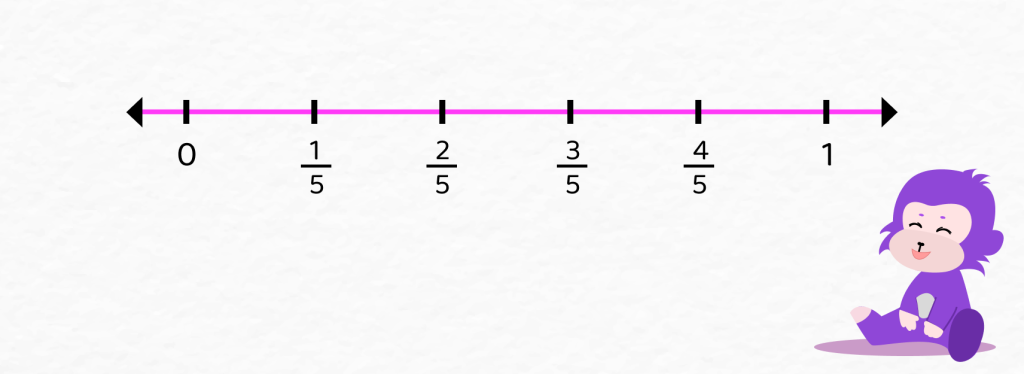
Fractions on a Number Line
Fractions can also be represented on a number line.
Fractions as Decimal
We can also represent fractions in the form of decimals by dividing the numerator by the denominator.
Do you want to make learning fun? Visit our site ChimpVine to learn and play.
Examples
Example 1: Represent 2/3 in the form of decimal
To convert 2/3 into decimal, we will have to divide 2 by 3, 2 ÷ 3 = 0.67
Example2: Segregate the fractions into proper and improper
2/3, 1/2, 2/7. 6/8, 3/2, 7/5, 8/3, 9/2
Proper Fractions: 2/3. 1/2, 6/8, 2/7
Impoper Fractions: 3/2, 7/5, 9/2, 8/3
Quiz
Tips and Tricks
1. Understanding Proper and Improper Fractions
Tip: A proper fraction has a numerator that is less than the denominator, while an improper fraction has a numerator that is greater than or equal to the denominator.
2. Converting Fractions to Decimals
Tip: To convert a fraction to a decimal, divide the numerator by the denominator. For example, 3/5 is equal to 0.6 when converted to a decimal.
3. Identifying Unit Fractions
Tip: A unit fraction has a numerator of 1. It represents the quantity of one part out of the total number of equal parts.
4. Comparing Mixed Numbers
Tip: When comparing mixed numbers, first compare the whole numbers. If the whole numbers are equal, compare the fractions to determine the greater value.
5. Exploring Equivalent Fractions
Tip: Equivalent fractions represent the same value, but they may look different. To find equivalent fractions, multiply or divide the numerator and denominator by the same number.
Real life application
Real-Life Applications
Scenario: “Sharing Pizza Slices”
In a real-life scenario, fractions are used to divide and share items equally among a group of people. For example, when sharing a pizza, each person may receive 1/4 of the pizza, representing an equal portion of the whole.
Scenario: “Measuring Ingredients in Recipes”
In cooking and baking, fractions are used to measure ingredients accurately. For instance, a recipe may require 1/2 cup of flour or 3/4 teaspoon of salt, where the fractions represent specific quantities.
Scenario: “Distance on a Map”
When using a map, fractions are used to represent distances. For example, if a map scale indicates 1 inch represents 10 miles, a distance of 2.5 inches on the map represents 25 miles in real life.
FAQ's
The different types of fractions include proper fractions, improper fractions, mixed numbers, and equivalent fractions.
A fraction consists of two parts: the numerator, which represents the number of parts being considered, and the denominator, which represents the total number of equal parts that make up a whole.
A unit fraction is a fraction where the numerator is 1. It represents the quantity of one part out of the total number of equal parts.
Fractions can be represented on a number line by dividing the line into equal parts based on the denominator and marking the position of the numerator.
To convert a fraction to a decimal, divide the numerator by the denominator. For example, 3/5 is equal to 0.6 when converted to a decimal.
By understanding the concept of fractions, their types, representations, and real-life applications, individuals can develop a strong foundation in mathematics and problem-solving skills. Fractions play a crucial role in various mathematical operations and are essential in everyday activities, making them a fundamental aspect of learning and understanding mathematics.
Like? Share it with your friends
Facebook
Twitter
LinkedIn