Understanding Ascending Order: Sorting Numbers in Ascending Order
Table of Contents
Introduction
Ascending Order
When dealing with numbers, especially in mathematics, the concept of ascending order plays a crucial role in sorting and organizing numerical values. Ascending order refers to the arrangement of numbers from the smallest to the largest. Let’s explore the significance of ascending order and its applications in various numerical contexts.
Analogy of Definition
What is Ascending Order?
Ascending order is a mathematical arrangement of numbers in increasing magnitude, from the smallest value to the largest value. It is denoted by the symbol “→” and is used to represent the order of integers, decimals, and fractions.
Method
Arranging Integers in Ascending Order
The order of integers differ in positive and negative integers. Let’s understand how they differ.
Positive Integers in Ascending Order
Arranging positive integers in ascending order involves considering their place values and magnitude. Here’s a simplified guide:
- Place Value Comparison: Begin by comparing the integers based on their place values. The number with fewer digits is smaller, while the one with more digits is larger.
- Leftmost Digit Comparison: If the number of digits is the same, compare the leftmost (highest place value) digits.
- Iterative Comparison: Continue this process for all integers until they are arranged from smallest to largest.
For example: Given integers: 245, 79, 1632, 512
79 is the smallest (two digits), and 8001 is the largest (four digits). Comparing 245 and 512, we compare their leftmost digits to determine their order. Finally, comparing 512 and 1632, we consider their digit count. Thus, the ascending order is: 79 < 245 < 512 < 1632
Negative Integers in Ascending Order
Organizing negative integers in ascending order requires understanding their behavior on the number line:
- Comparison Principle: If integer a is greater than integer b (a > b), then the opposite of a, denoted as (-a), is less than the opposite of b, (-b). This is because moving left on the number line (subtracting) results in a smaller value.
- Application of Rule: Conversely, if a is less than b (a < b), then (-a) is greater than (-b). This aligns with the concept that a smaller negative integer (-a) is positioned to the right of a larger negative integer (-b) on the number line.
By adhering to these principles, we can effectively arrange negative integers in ascending order.
For instance: Given negative integers: -17, -5, -31, -68
Comparing -5 and -17, -17 is smaller, indicating -5 > -17. Similarly, comparing -31 and -68, -68 is smaller, showing -31 > -68. Thus, arranging them in ascending order yields: -68 < -31 < -17 < -5.
Ascending Order on a Number Line
A number line is a visual representation of numbers, and arranging numbers in ascending order on a number line involves plotting the values from left to right in increasing order. It is the easiest way to understand the concept of ascending order.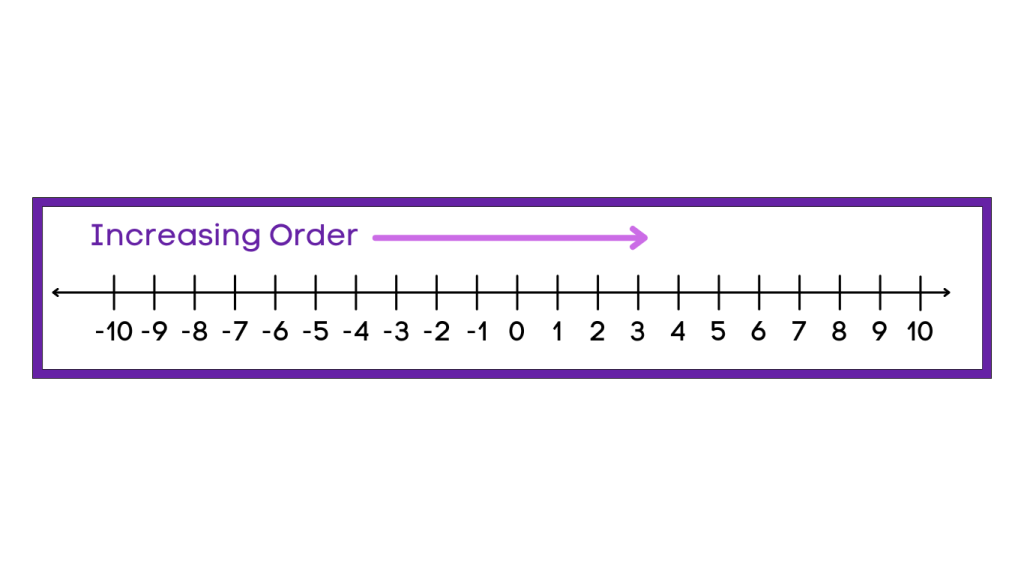 
Ascending Order for Decimals
When arranging decimals in ascending order, you compare the place values to determine the order from the smallest to the largest decimal. We begin from checking from the left-most digit and if they match we move to the next digit, and if one digit is greater than the other in the same place value, we know that the number is greater.
Arranging 0.32, o.54, 0.25, 0.12
Step 1: Comparing the left-most digit, i.e. 0, which is the same in all the numbers.
Step 2: Comparing the next digit, 5 is the greatest, so 0.54 is the highest number.
Step 3: After 5, the greatest one is 3, so 0.34 is the second highest number.
Step 4: In the similar manner, we check the other digits, and get the order 0.12 < 0.25 < 0.32 < 0.54
Ascending Order for Fractions
To arrange fractions in ascending order, you compare the numerical values of the fractions and place them in increasing order based on their magnitudes.
Ascending Order for Like fractions
The fractions whose denominator are same are known as like fractions. Such fractions can be put in ascending order by comparing the numerators.
For example: Arranging the fractions \frac{1}{3}, \frac{5}{3}, \frac{2}{3}, \frac{7}{3}
Let’s arrange the numerators in ascending order, 1 → 2 → 5 → 7, which will be \frac{1}{3}, \frac{2}{3}, \frac{5}{3}, \frac{7}{3}
Ascending Order for Unlike Fractions
The fractions with diferent denominators are known as unlike fractions. To arrange such fractions in ascending order, we will have to convert them into like fractions by finding out the LCM of the denominators. Then, we will compare the numerators to arrange in ascending order.
For example: Arranging the fractions \frac{1}{2}, \frac{5}{4}, \frac{2}{6}, \frac{7}{8}
Step 1: We need to find the LCM of the numbers 2, 4, 6 and 8, which is 24.
Step 2: Converting the fractions to like we get \frac{12}{24}, \frac{30}{24}, \frac{8}{24}, \frac{21}{24}
Step 3:We will then arrange the numerator in ascending order 8 → 12 → 21 → 30
Step 4: Now will we put the numbers in their fraction forms, which will give us \frac{8}{24}, \frac{12}{24}, \frac{21}{24}, \frac{30}{24}
Examples
Example 1: Arranging the integers 8, 3, 6, and 10 in ascending order.
Arranged in ascending order: 3, 6, 8, 10
Example 2: Plotting the integers 1, 4, 7, and 10 in ascending order on a number line.
Number line: 1 → 4 → 7 → 10
Example 3: Arranging the decimals 0.25, 0.1, 0.5, and 0.75 in ascending order.
Arranged in ascending order: 0.1, 0.25, 0.5, 0.75
Quiz
Tips and Tricks
1. Start with the smallest
Tip: When arranging items in ascending order, always begin with the smallest item and then proceed to the next smallest one. This ensures that you’re building up the order correctly.
2. Compare adjacent items
Tip: If you’re arranging a list manually, compare each item with the one next to it. If the current item is smaller than the next one, they’re in the right order. If not, swap their positions.
3. Understand numerical order
Tip: Remember that in ascending order, numbers go from the smallest to the largest. Keep this in mind when arranging numerical data.
4. Consider alphabetical order
Tip: When dealing with text or strings, ascending order follows alphabetical order. A helpful tip is to remember that lowercase letters come before uppercase letters.
5. Double-check your work
Tip: After arranging items, take a moment to double-check your work. Scan through the list to ensure that everything is in the correct order, especially if you sorted the data manually.
Real life application
Story: “The Ascending Order Adventure of Sam and Maya”
Sam and Maya were two adventurous friends who loved exploring the world of mathematics. They encountered various real-life scenarios where the concept of ascending order played a crucial role in solving everyday challenges.
Challenge 1: The Grocery Shopping Quest
Sam and Maya went grocery shopping and needed to arrange the prices of different items in ascending order to compare and budget their expenses. By arranging the prices from the smallest to the largest, they were able to make informed decisions and manage their shopping list effectively.
Challenge 2: The Travel Itinerary Puzzle
As they planned a trip, Sam and Maya had to arrange the departure times of flights and train schedules in ascending order to create a seamless travel itinerary. By organizing the timings from the earliest to the latest, they ensured a smooth and well-coordinated journey.
Challenge 3: The Recipe Ingredient Arrangement
In the kitchen, Sam and Maya arranged the quantities of ingredients in ascending order to follow recipes accurately and maintain a systematic approach to cooking. By organizing the ingredients from the smallest to the largest, they achieved precision and efficiency in their culinary endeavors.
FAQ's
Arranging numbers in ascending order is essential for comparison, organization, and analysis of numerical values. It helps in identifying the smallest and largest values, making it easier to interpret data and make informed decisions.
Yes, the methods for arranging decimals and fractions in ascending order involve comparing the numerical values and placing them in increasing order based on their magnitudes. This allows for a systematic arrangement of decimal and fractional values.
Ascending order facilitates data analysis by providing a structured arrangement of numerical values, making it easier to identify patterns, trends, and outliers. It enables informed decision-making by highlighting the smallest and largest values for comparison and evaluation.
Yes, ascending order can be used for arranging non-numeric items such as words, letters, or objects based on their characteristics or properties. For example, arranging names alphabetically or sorting books by author’s last name.
The opposite of ascending order is descending order, which arranges items or numbers from the largest to the smallest.
Like? Share it with your friends
Facebook
Twitter
LinkedIn