Least Common Multiple (LCM) – Methods and Examples
Table of Contents
Introduction
Least Common Multiple (LCM)
When dealing with numbers, especially in mathematics, you often come across the term “Least Common Multiple” or LCM. But what exactly does it mean? Let’s dive into the world of LCM and understand its significance in solving mathematical problems.
Analogy of Definition
What is Least Common Multiple (LCM)?
The Least Common Multiple (LCM) of two or more numbers is the smallest multiple that is exactly divisible by each of the numbers. In simpler terms, it is the smallest number that is a multiple of all the given numbers.
Method
Methods of Finding Least Common Multiple (LCM)
There are various methods to find the least common multiple (LCM) of numbers.
LCM by Listing Method
One common method is to list the multiples of each number and find the smallest multiple that is common to all the numbers.
Example: Find the LCM of 9 and 12
Muliple of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90
Multiples of 12: 12, 24, 36, 48, 60, 72, 84,96, 108,120
The lowest common mutiple is 26, so LCM = 36
LCM by Prime Factorization
Another method involves using prime factorization to find the LCM. To find the least common multiple (LCM), we write the prime factors of the numbers in the exponent form and the factors with the highest exponent is the LCM.
Example: Find the least common multiple of 18 and 24
Prime factorization of 18: 3*3*2 = 32 * 21
Prime factorization of 24: 2*2*2*3 = 23 *31
Hence, LCM = 32 * 23 = 9 * 8 = 72
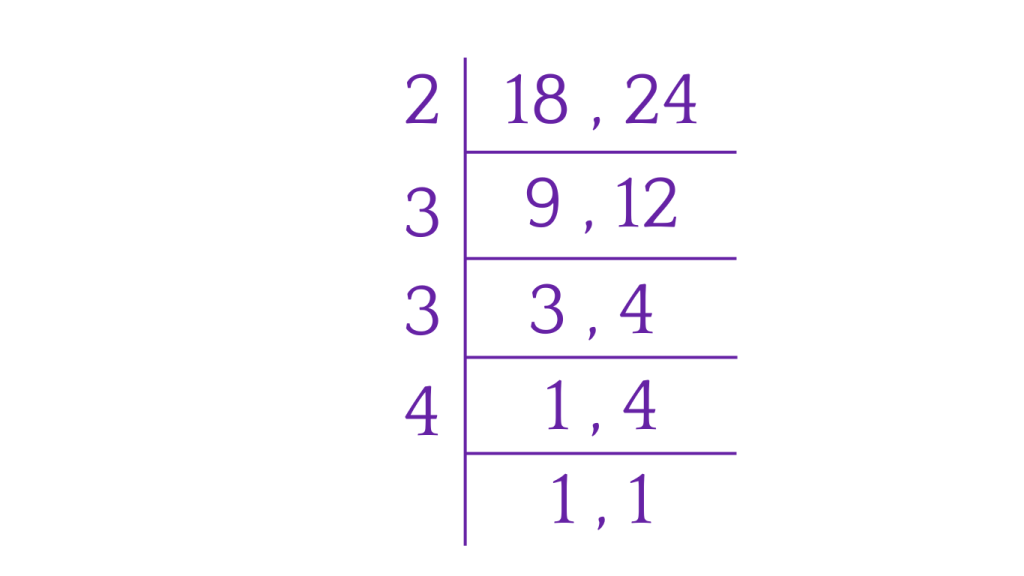
LCM by Division Method
The division method can also be used to find the least common multiple (LCM) of numbers.
Example: Find the LCM of 18 and 24
Step 1: The lowest prime factor of 18 and 24 is 2, so we write 2 on the left and write numbers that divide the numbers on the right below it.
Step 2: 2 divides both 18 and 24. In the next step we look for the lowest prime factor of 6 and 9, which is 3 , we continue to do the same till we get 1 as the quotient in the last row.
Engage in learning LCM in a fun and interesting way with ChimpVine.
Examples
Finding the Least Common Multiple (LCM) of 12 and 15
Step 1: List the multiples of each number
Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, …
Multiples of 15: 15, 30, 45, 60, 75, 90, 105, 120, …
Step 2: Identify the smallest common multiple
The least common multiple of 12 and 15 is 60.
So, the LCM of 12 and 15 is 60.
Quiz
Tips and Tricks
1.Prime Factorization Method
Tip: Break down each number into its prime factors, then identify the highest power of each prime factor that appears in any of the numbers. Multiply these highest powers together to find the LCM.
2.Using GCD (Greatest Common Divisor):
Tip: Utilize the relationship between LCM and GCD, which states that LCM(a, b) = (a * b) / GCD(a, b). First, find the GCD of the numbers using any method, then use this formula to calculate the LCM easily.
3.Listing Multiples
Tip: Write down the multiples of each number until you find a common multiple. The smallest common multiple is the LCM.
4.Using the Prime Factorization Table
Tip: Create a table listing the prime factors of each number and their powers. The LCM is obtained by taking the product of the highest power of each prime factor.
5.Using Prime Numbers
If both numbers are prime, the LCM is simply their product.
Real life application
Story: “The Least Common Multiple (LCM) Adventure of Alex and Lily”
Alex and Lily were two adventurous siblings who loved solving puzzles and riddles. One day, they encountered a series of challenges that required them to use the concept of LCM to overcome obstacles and complete their quests.
Challenge 1: The Treasure Hunt
Alex and Lily embarked on a treasure hunt that led them to a mysterious cave. Inside the cave, they found a locked chest with a riddle written on it. The riddle stated, “To open the chest, find the least number that is a multiple of 4, 6, and 8.” Remembering their lessons on LCM, Alex and Lily quickly calculated the LCM of 4, 6, and 8, which turned out to be 24. They used the number to unlock the chest and discovered a map to the hidden treasure.
Challenge 2: The Magical Bridge
As they continued their adventure, Alex and Lily encountered a magical bridge guarded by a mystical creature. The creature challenged them to find the least number of steps that would cause the bridge to light up. The steps were numbered 5, 7, and 9. Applying their knowledge of LCM, Alex and Lily calculated the LCM of 5, 7, and 9, which turned out to be 315. As they took 315 steps, the bridge lit up, allowing them to cross safely.
Challenge 3: The Enchanted Garden
In the final challenge, Alex and Lily entered an enchanted garden filled with beautiful flowers. They were tasked with arranging the flowers in rows, with each row containing 12, 15, and 18 flowers. Using the concept of LCM, they determined that they needed 180 flowers to fill each row without any flowers left over. The garden bloomed with vibrant colors, and the siblings completed their adventure successfully.
FAQ's
Finding the LCM is important in various mathematical and real-life scenarios. It helps in solving problems related to scheduling, repeating patterns, and resource allocation. In mathematics, the LCM is used in operations involving fractions, simplifying expressions, and solving equations.
The LCM is directly related to the concept of multiples. It represents the smallest common multiple of two or more numbers. Multiples are the result of multiplying a number by an integer, and the LCM is the smallest multiple that is common to all the given numbers.
Yes, the LCM is used to find the common denominator when adding or subtracting fractions. By finding the LCM of the denominators, you can convert the fractions to equivalent fractions with the same denominator, making it easier to perform operations.
There are different methods to find the LCM, including listing multiples, using prime factorization, and using the method of division. Each method has its advantages and can be applied based on the given numbers and the preferred approach.
The concept of LCM has practical applications in various real-life situations, such as scheduling events, planning recurring tasks, and organizing resources. It helps in determining the least amount of time, distance, or quantity needed to fulfill specific requirements, making it a valuable tool in problem-solving.
Like? Share it with your friends
Facebook
Twitter
LinkedIn