Comparing Fractions: Exploring Methods and Applications
Table of Contents
Introduction
Comparing Fractions
In the realm of mathematics, the skill of comparing fractions plays a pivotal role in understanding their relative magnitudes and making informed decisions. Let’s delve into the methods of comparing fractions and explore their practical applications in real-life contexts.
Analogy of Definition
How to Compare Fractions?
Comparing fractions involves determining the relative sizes of two or more fractions and identifying which fraction is larger, smaller, or if they are equal in value.
Method
Methods for Comparing Fractions
There are several methods to compare fractions, including finding a common denominator, converting to decimals, and using visual representations such as fraction bars or circles.
Comparing Fractions with Like Denominator
If the denominators of the fractions are the same, or if the fractions are like fractions, then comparing them becomes simple. All we have to do to compare like fractions are to look at the numerator. The fraction with the higher number numerator will be the greater fraction. Let’s look at an example
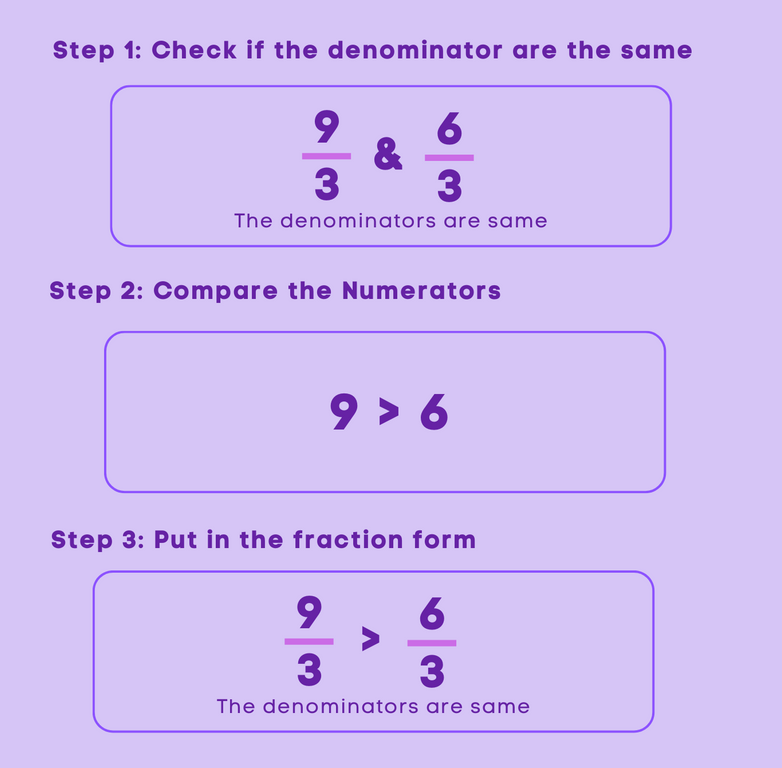
Comparing Unlike Fractions
The fractions with diferent denominators are known as unlike fractions. To compare such fractions, we will have to convert them into like fractions by finding out the LCM of the denominators. Then, we will compare the numerators like we did for like fractions.
For example: Comparing the fractions \frac{2}{6} and \frac{7}{8}

Comparing Decimals
We can compare fractions by converting it into decimals. To convert the fractions to decimal, we need to divide the numerator by the denominator. Then, we compare the decimals.
Let’s compare \frac{2}{6} and \frac{7}{8}
Step 1: Convert the fractions into decimals. \frac{2}{6} = 0.33 and \frac{7}{8} = 0.87
Step 2: Compare the decimal numbers, 0.87 > 0.33
Step 3: Since 0.87 > 0.33, \frac{7}{8} > \frac{2}{6}
Examples
Example 1:
Scenario: Comparing 3/4 and 5/8
Method: Finding a common denominator
Calculation: 3/4 = 6/8, 5/8
Comparison: 6/8 > 5/8
Conclusion: 3/4 is greater than 5/8.
Example 2:
Scenario: Comparing 1/3 and 2/5
Method: Converting to decimals
Calculation: 1/3 ≈ 0.333, 2/5 = 0.4
Comparison: 0.333 < 0.4
Conclusion: 1/3 is less than 2/5.
Example 3:
Scenario: Comparing 2/7 and 3/9
Method: Visual representation using fraction bars
Comparison: 2/7 is visually smaller than 3/9
Conclusion: 2/7 is less than 3/9.
These examples illustrate the methods of comparing fractions, including finding a common denominator, converting to decimals, and using visual representations. By applying these methods, the relative sizes of fractions can be determined, enabling informed comparisons and decision-making in various mathematical contexts and real-life scenarios.
Quiz
Tips and Tricks
1. Common Denominator Method
Tip: Find a common denominator for both fractions, then compare the numerators. For example, to compare \frac{1}{3} and \frac{2}{5} , find a common denominator (15 in this case), then compare \frac{5}{15} and \frac{6}{15} . Since \frac{6}{15} is greater than \frac{5}{15} , \frac{2}{5} is greater than \frac{1}{3} .
2. Cross Multiplication Method
Tip: Multiply the numerator of the first fraction by the denominator of the second fraction, and vice versa. Then compare the results. For example, to compare \frac{1}{3} and \frac{2}{5} , cross multiply to get 5 × 1 = 5 and 3 × 2 = 6. Since 6 is greater than 5, \frac{2}{5} is greater than \frac{1}{3} .
3. Visualize on a Number Line
Tip: Represent each fraction on a number line. This can help visualize which fraction is greater. For example, if you represent \frac{1}{3} and \frac{2}{5} on a number line from 0 to 1, you’ll see that \frac{2}{5} is closer to 1 than \frac{1}{3} , making it greater.
4. Convert to Decimals
Tip: Convert both fractions to decimals and then compare them. For example, \frac{1}{3} ≈ 0.333 and \frac{2}{5} ≈ 0.4. Since 0.4 is greater than 0.333, \frac{2}{5} is greater than \frac{1}{3} .
5. Benchmark Fractions
Tip: Know some benchmark fractions (like 1/2, 1/3, 1/4, etc.) and use them as references. For example, if you’re comparing \frac{1}{3} and \frac{3}{4} you know that \frac{1}{3} is smaller than \frac{1}{2} , and \frac{3}{4} is greater than \frac{1}{2} , so \frac{3}{4} must be greater than \frac{1}{3} .
Real life application
Scenario: Recipe Adjustments
When adjusting a recipe to serve a larger or smaller number of people, the skill of comparing fractions is utilized to proportionally increase or decrease ingredient quantities while maintaining the recipe’s integrity.
Scenario: Budget Planning
In budget planning, comparing fractions helps in allocating resources and expenses proportionally, ensuring that each category receives the appropriate share of the budget.
Scenario: Art and Design
In art and design, understanding and comparing fractions is essential for creating visually appealing compositions and determining proportions in various artistic elements.
FAQ's
Like? Share it with your friends






