Decimals – Definition, Types, Properties and Examples
Table of Contents
Introduction
Decimals
Decimals are an essential part of mathematics, representing a way to express numbers that fall between whole numbers. They are used in various real-life scenarios, from measuring quantities to representing parts of a whole. In this article, we will dive into the different types of decimals, their properties, and the operations involved in working with decimals.
Analogy of Definition
What are Decimals?
Decimals are a way of expressing numbers that are not whole. A decimal number has a whole number and a fractional part, which is separated by a dot in between.They can be divided into two main types: recurring decimals, where the digits repeat indefinitely, and non-recurring decimals, where the digits do not repeat. Decimals can also be converted to fractions, and vice versa, providing a versatile way to represent numerical values. Decimal Place Values helps us to understand the value of each digit that follows the decimal.
Method
Types of Decimals
Recurring Decimals (Repeating or Non – Terminating Decimals)
Recurring decimals are numbers that have a repeating pattern of digits after the decimal point. For example, 0.3333… is a recurring decimal, as the digit 3 repeats infinitely. Recurring decimals are often represented using a bar over the repeating digits, such as 0.3̅.
Non – Recurring Decimals (Non – Repeating ot Terminating Decimals)
Non-recurring decimals are numbers that do not have a repeating pattern of digits after the decimal point. For example, 0.275 is a non-recurring decimal, as the digits 2, 7, and 5 do not repeat in a pattern. Non-recurring decimals are also known as terminating decimals, as they have a finite number of decimal places.
Converting Decimals to Fractions
Decimals can be converted to fractions by using their place value. For example, the decimal 0.45 can be expressed as the fraction 9/20, a 4 and 5 represent the tenths and hundredths places, respectively. This conversion allows for easy comparison and manipulation of decimal values. We can convert a decimal number by expanding it based on its decimal place value and simplifying it.
For example: Converting 0.45 to fraction
0.45 = 45 * 1/100 = 45/100 = 9/20
Converting Fractions to Decimals
We can use division to convert fractions to decimlas. We have to divide the numerator by the denominator to get the number in decimal form. We can use the method of long division for the conversion.
For example: Converting 9/20 to decimal
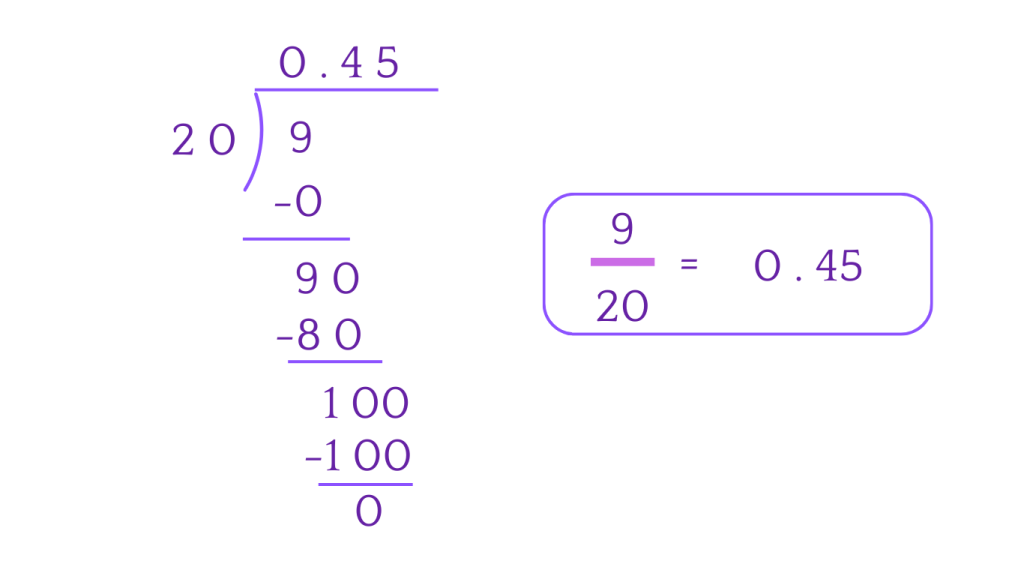
Properties of Decimals
Decimals exhibit various properties that make them unique in mathematical operations. They can be added, subtracted, multiplied, and divided, following specific rules and properties that govern their behavior. Understanding these properties is crucial for working with decimals effectively.
Addition and Subtraction of Decimals
When adding or subtracting decimals, it is important to align the decimal points to ensure accuracy. The digits in the same place value are then added or subtracted accordingly. For example, when adding 3.25 and 1.6, the decimal points are aligned, and the digits are added to yield the sum of 4.85.
Multiplying and Dividing Decimals
In multiplication and division of decimals, the number of decimal places in the product or quotient is determined by the total number of decimal places in the factors or dividend and divisor. The method of dividing and multiplying is same as that of integer numbers. The decimal point is then placed in the result according to the calculated number of decimal places.
Examples
Example 1: Adding Decimals
Add 12.36 and 5.8
Solution:
Multiplying Decimals
Multiply 3.25 and 3
Solution:
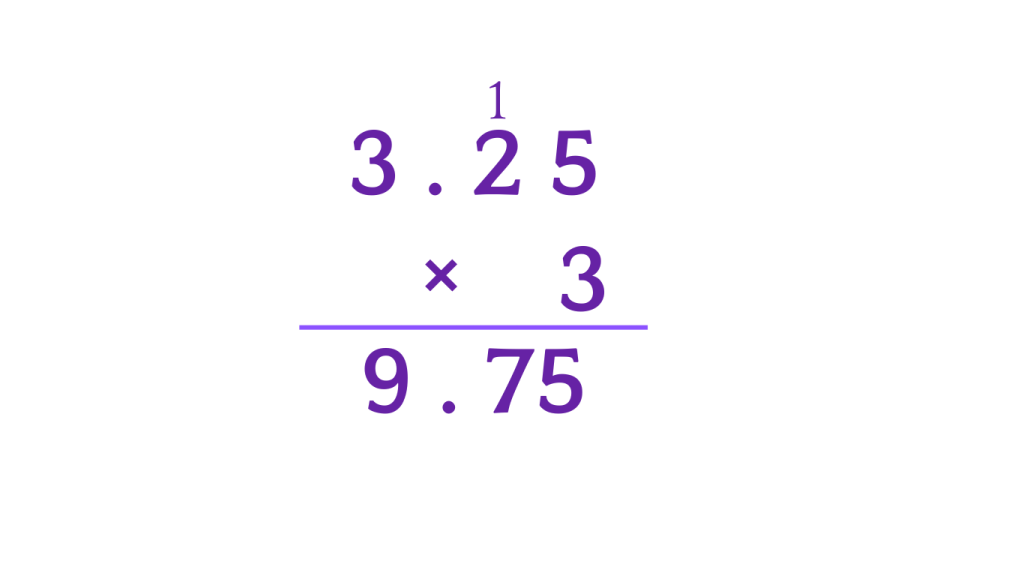
Quiz
Tips and Tricks
1. Subtraction of Decimals
Tip: When subtracting decimals, align the decimal points and subtract the digits in the same place value to get the correct result.
2. Multiplication of Decimals
Tip: When multiplying decimals, count the total number of decimal places in the factors and place the decimal point in the product accordingly.
3. Division of Decimals
Tip: When dividing decimals, determine the number of decimal places in the quotient based on the total decimal places in the dividend and divisor.
Real life application
Story: “The Decimals Adventure of Maya and Ethan”
Maya and Ethan, two curious students, embarked on an adventure to explore the practical applications of decimals in everyday life. They encountered various challenges that required them to apply their knowledge of decimals to solve real-world problems.
Challenge 1: The Money Management Quest
Maya and Ethan were tasked with managing a budget for a school event. They had to calculate the total cost of supplies, including items priced at $3.25, $5.50, and $7.75. By adding and subtracting decimals, they determined the remaining budget for additional expenses.
Challenge 2: The Recipe Experiment
In their next challenge, Maya and Ethan experimented with a recipe that required 1.5 cups of flour. They needed to adjust the recipe to make half the amount, requiring them to multiply decimals and convert fractions to decimals to accurately measure the ingredients.
Challenge 3: The Shopping Spree Puzzle
As part of their adventure, Maya and Ethan went on a shopping spree with a budget of $100. They had to calculate the cost of items priced at $12.50 each and determine the maximum number of items they could purchase, applying the concept of division of decimals.
FAQ's
Decimals can be categorized into recurring decimals, where the digits repeat indefinitely, and non-recurring decimals, where the digits do not repeat. They can also be represented as fractions, providing a versatile way to express numerical values.
When adding or subtracting decimals, it is important to align the decimal points and perform the addition or subtraction of digits in the same place value to obtain the correct result.
Decimals can be converted to fractions by using their place value, while fractions can be converted to decimals by performing the division of the numerator by the denominator. These conversions provide a flexible way to represent numerical values in different forms.
Applications of decimals in daily life are numerous and essential for precise representation of values. Decimals are essential in daily finances, from calculating exact purchase amounts to handling currency conversions and managing account balances. They ensure precision in monetary transactions, enabling accurate financial decisions. Other applications of decimals could be in reading temperatures, health and medicine, academic grading and many more.
A decimal is a numerical system that includes a decimal point to represent parts of a whole, with digits extending to the right of the decimal point.
Like? Share it with your friends
Facebook
Twitter
LinkedIn