Understanding Acute Angles
Table of Contents
Introduction
What are Angles?
In geometry, an angle is a fundamental concept that describes the measure of the amount of rotation needed to bring one line or plane into coincidence with another. Angles are formed when two rays (or line segments) share a common endpoint, known as the vertex. These rays extend outward from the vertex to create the shape of the angle.
Components of an Angle
Vertex: The common endpoint of the two rays that form the angle. It is represented by a single point where the rays meet.
Arms: The two rays that extend outward from the vertex. Each ray contributes to the shape and measure of the angle.
Types of Angles
Angles can be classified based on their measure and characteristics:
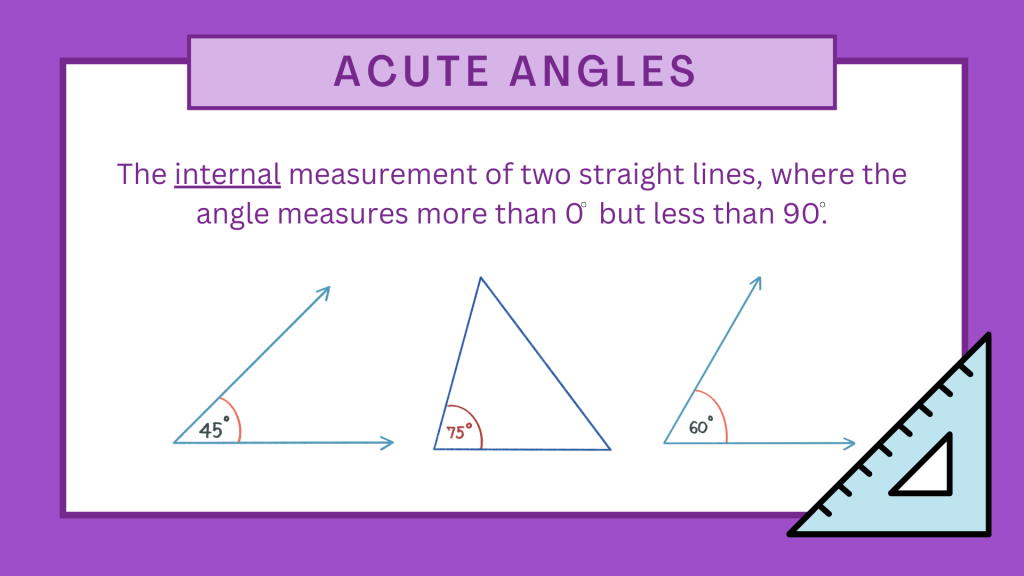
Acute Angle: An angle that measures greater than 0 degrees and less than 90 degrees. It is characterized by its sharpness.
Right Angle: An angle that measures exactly 90 degrees. It forms a perfect “L” shape.
Obtuse Angle: An angle that measures greater than 90 degrees and less than 180 degrees. It is wider than a right angle but narrower than a straight angle.
Straight Angle: An angle that measures exactly 180 degrees. It forms a straight line.
Reflex Angle: An angle that measures greater than 180 degrees and less than 360 degrees. It extends beyond a straight angle.
Full Angle: An angle that measures exactly 360 degrees. It represents a complete revolution.
Analogy of Definition
What are Acute Angles?
Acute Angles are angles that measure less than 90 degrees, and they are commonly found in geometric shapes and trigonometric calculations. In simpler terms, they represent the sharp angles that are less than a right angle.
Method
Properties of Acute Angles
The properties of Acute Angles include their measurement being less than 90 degrees, their presence in right-angled triangles, and their significance in determining the acute triangle. Let’s understand acute angles more clearly.
Size: Acute angles always measure between 0 degrees and 90 degrees. They are characterized by their sharpness and do not extend beyond a right angle (90 degrees).
Shape: Acute angles are characterized by their sharp and narrow appearance. When drawn, they resemble a small “v” shape, with the vertex at the center and the rays extending outward.
Triangle Classification: In a triangle, if all three angles are acute, the triangle is classified as an acute triangle. This means that all angles in the triangle measure less than 90 degrees.
Complementary Angles: Acute angles are complementary to obtuse angles, meaning that when combined, their measures add up to 90 degrees. For example, if one angle measures 30 degrees, its complementary angle measures 60 degrees.
Examples
Example 1: In a triangle with angles measuring 30, 60, and 90 degrees, the angles measuring 30 and 60 degrees is an Acute Angle.
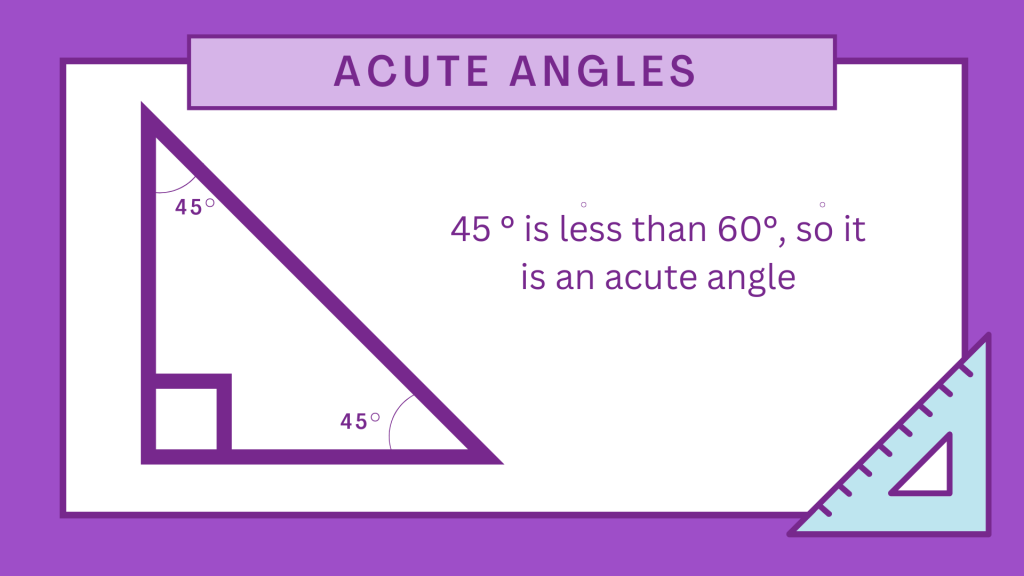
Example 2: In a right-angled triangle with angles measuring 45, 45, and 90 degrees, both angles measuring 45 degrees are Acute Angles.
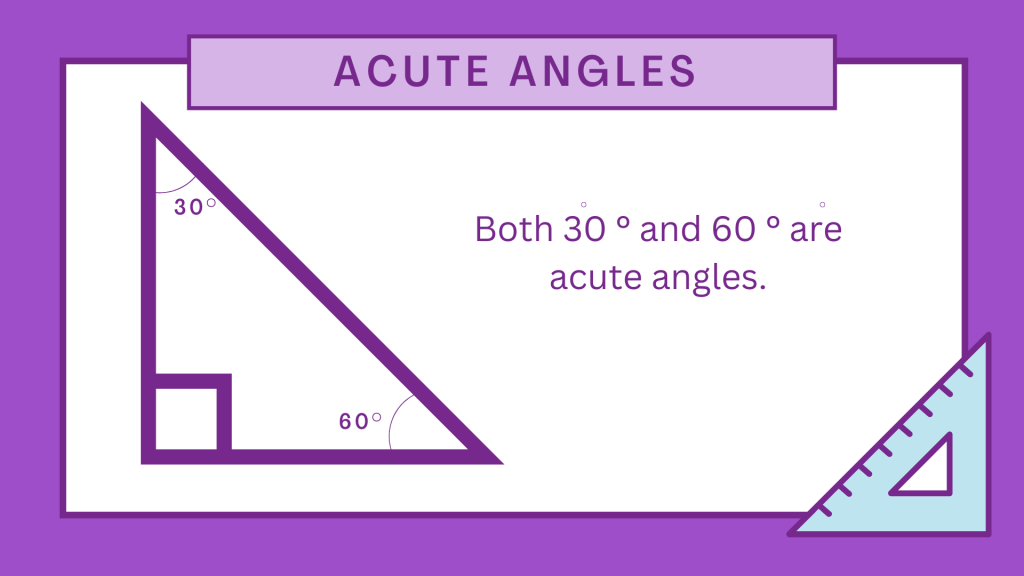
Example 3: In an equilateral triangle with all angles measuring 60 degrees, all angles are Acute Angles.
Summary::
These examples demonstrate the presence of Acute Angles in different types of triangles, showcasing their significance in determining the nature of angles within geometric shapes. By understanding the properties and measurements of Acute Angles, one can effectively analyze and solve various mathematical and real-life problems.
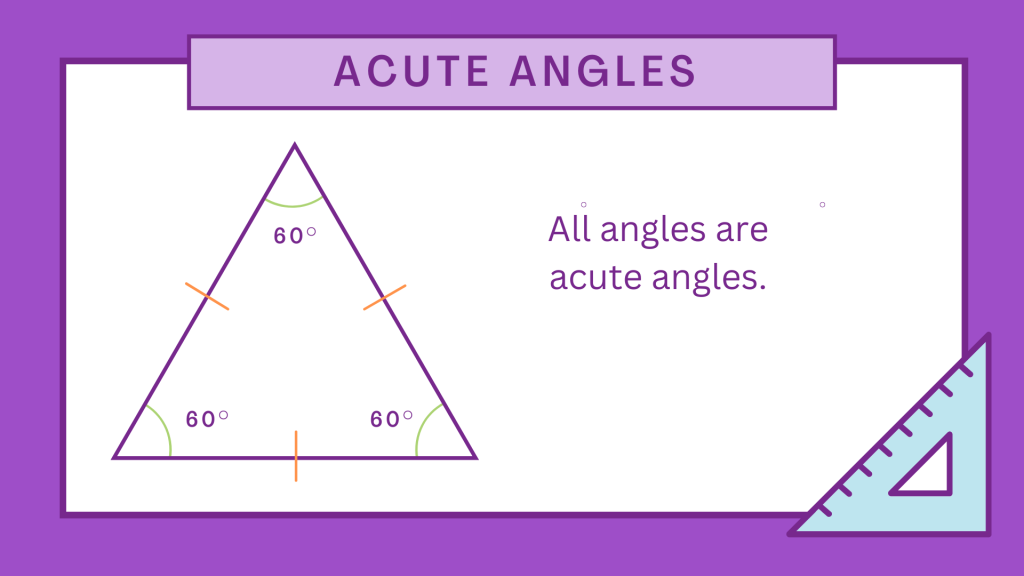
These examples demonstrate the presence of Acute Angles in different types of triangles, showcasing their significance in determining the nature of angles within geometric shapes. By understanding the properties and measurements of Acute Angles, one can effectively analyze and solve various mathematical and real-life problems.
Quiz
Tips and Tricks
1. Identifying Acute Angles
Tip: To identify Acute Angles, look for angles that measure less than 90 degrees within geometric shapes and trigonometric calculations.
2. Calculating Acute Angles in Triangles
Tip: In triangles, identify angles that measure less than 90 degrees to determine the presence of Acute Angles and their significance in the triangle’s properties.
3. Real-Life Applications of Acute Angles
Tip: Explore the application of Acute Angles in architectural design, engineering calculations, and navigation systems to understand their practical significance.
Real life application
Scenario: Architectural Design
Architects utilize the concept of Acute Angles in designing structures with sharp angles and precise measurements, ensuring stability and aesthetic appeal
Scenario: Engineering Calculations
Engineers apply the understanding of Acute Angles in calculating the angles of intersecting beams and trusses, optimizing the structural integrity of buildings and bridges.
Scenario: Navigation Systems
Navigation systems incorporate the concept of Acute Angles in determining the direction and angle of travel, facilitating accurate and efficient navigation for various modes of transportation.
FAQ's
Understanding Acute Angles is crucial as it helps in various mathematical and geometric calculations, as well as in real-life applications such as architecture and engineering.
Acute Angles are defined as angles that measure between 0 and 90 degrees, and they are commonly found in geometric shapes and trigonometric calculations.
The properties of Acute Angles include their measurement being less than 90 degrees, their presence in right-angled triangles, and their significance in determining the acute triangle.
Yes, Acute Angles can be classified into different types based on their measurements, such as acute, right, and obtuse angles, each with distinct characteristics and applications.
The concept of Acute Angles finds practical applications in various real-life scenarios such as architectural design, engineering calculations, and navigation systems.
Like? Share it with your friends
Facebook
Twitter
LinkedIn