Understanding Alternate Interior Angles: Definition and Properties
Table of Contents
Introduction
Alternate Interior Angles
In the realm of geometry, the concept of alternate interior angles holds significant importance. Let’s delve into the definition and properties of alternate interior angles to gain a comprehensive understanding of their role in geometric configurations.
Analogy of Definition
What are Alternate Interior Angles?
Alternate interior angles are a pair of angles that are formed when a transversal intersects two lines. They are located on opposite sides of the transversal and inside the two lines, creating a distinct geometric relationship.
Let’s understand the concept of alternate interior angles in a simple manner.
Alternate interior angles are like secret buddies hiding within parallel lines that get crossed by another line (usually called a transversal).
Imagine two parallel lines with a third line crossing through them. Where the third line cuts through the first two, it creates four angles. Alternate interior angles are the ones on the inside, but opposite sides of the transversal. They’re like a pair of cousins sitting across from each other at a dinner table, but in geometry!
These angles have a special relationship: they’re always equal. So, if you measure one of them, you’ll find that the other one has the same measurement. It’s like they’re twins – whatever one does, the other follows suit.
This concept is super handy because it helps us solve all sorts of geometry problems, from figuring out angles in shapes to understanding how lines intersect.
Method
Identifying Alternate Interior Angles
To identify alternate interior angles, one must recognize the pattern of their positioning when a transversal intersects two lines. Understanding the properties and congruence of these angles is essential in various geometric applications.
Here’s a simple step-by-step guide to spot alternate interior angles:
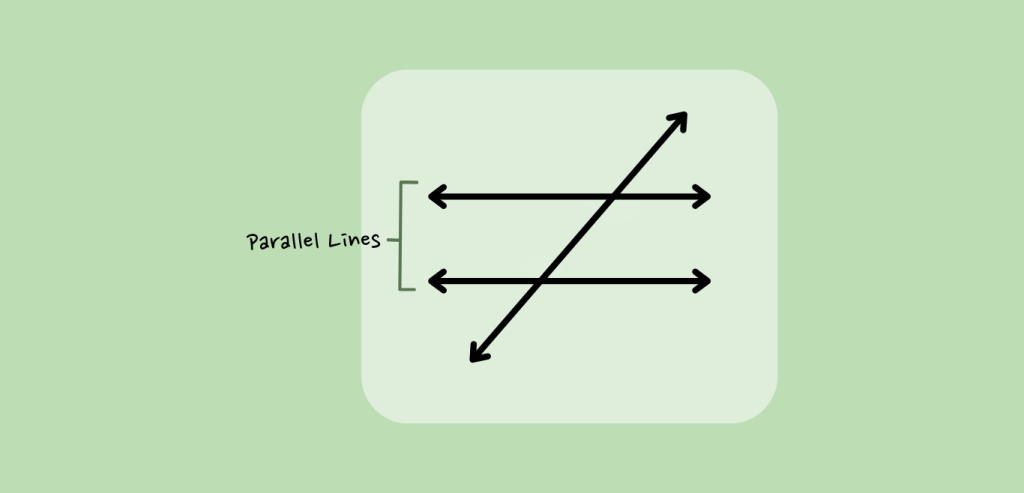
Find Parallel Lines: First, look for two lines that are parallel to each other. They should be like train tracks – never crossing each other, but running side by side.
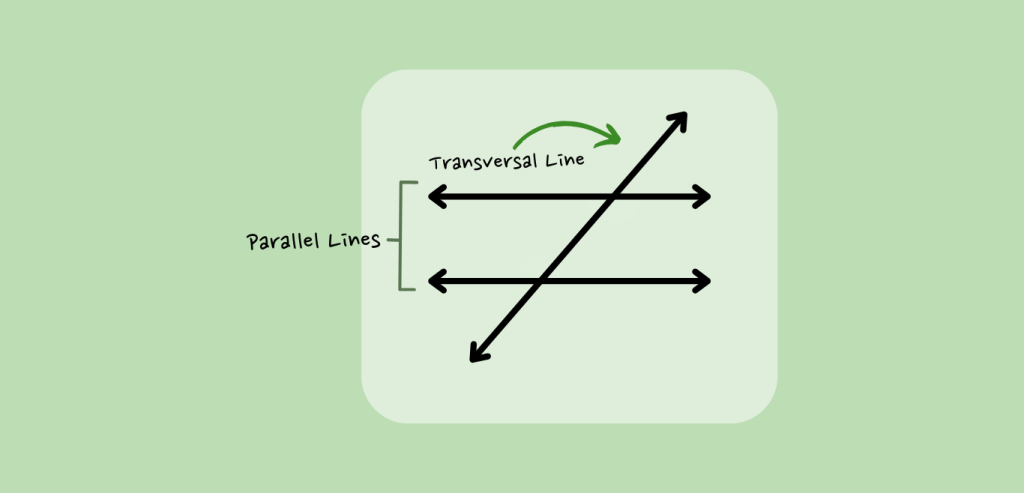
Locate the Transversal: Next, find another line that crosses (or intersects) those parallel lines. This line is called the transversal.
Identify Interior Angles: Now, focus on the angles formed on the inside of the parallel lines, but on opposite sides of the transversal. These are your alternate interior angles.
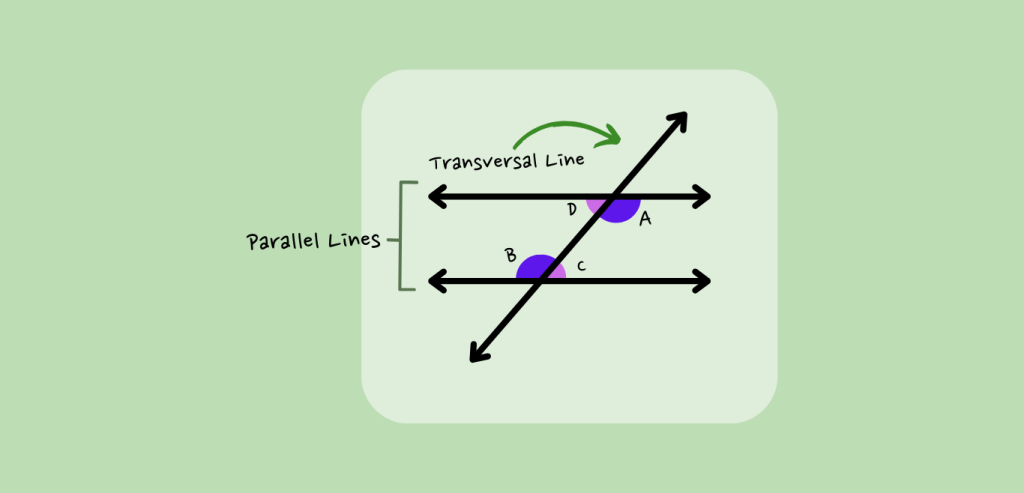
Check for Equality: Remember, alternate interior angles are always equal. So if you measure one angle and find its value, you’ll see that the other alternate interior angle has the same measurement.
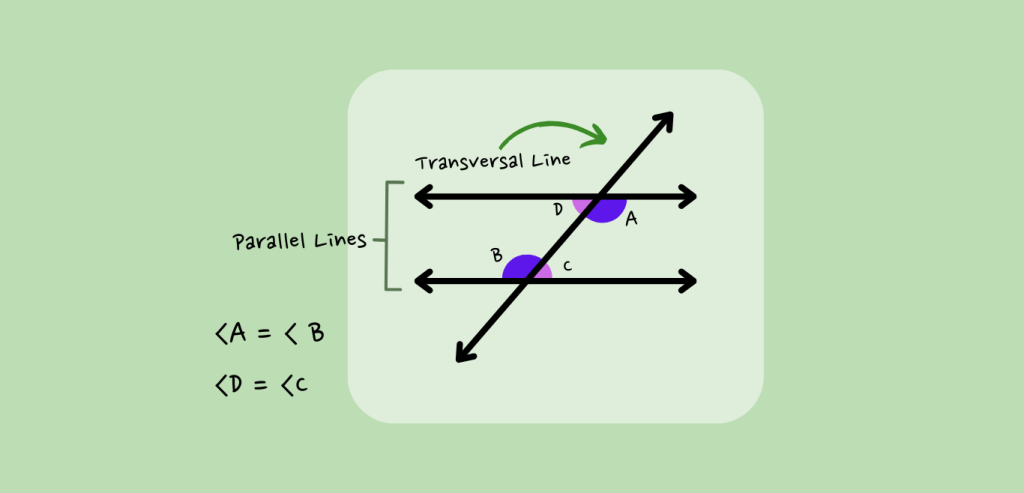
Keep in mind this neat trick: if you have parallel lines and a transversal, and you spot equal interior angles on one side of the transversal, you can bet there are equal alternate interior angles hiding on the other side!
Examples
Example: Find the value of X and Y in the given figure
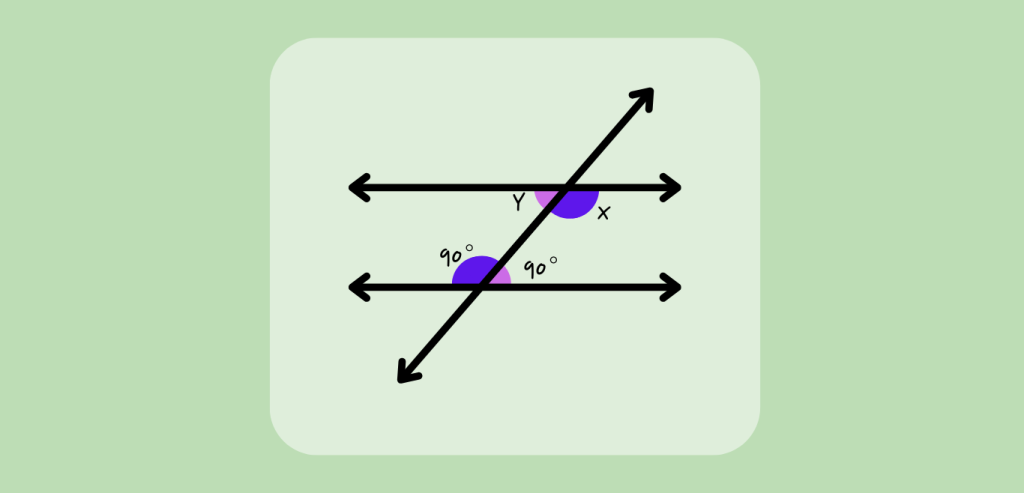
We know that,
The alternate interior angle of ∠X is 90°, so ∠X = 90°.
Similarly,
The alternate interior angle of ∠Y is 90°, so ∠X = 90°.
Summary: This example illustrates the process of identifying and understanding alternate interior angles in the context of parallel lines intersected by a transversal. By recognizing the congruence and properties of alternate interior angles, one can effectively analyze geometric configurations and make accurate deductions.
Quiz
Tips and Tricks
1. Angle Measurement
Tip: When lines are parallel, alternate interior angles are congruent, allowing for the calculation of angle measures based on known values.
2. The Architect’s Blueprint
Tip: Utilize the properties of alternate interior angles to ensure the symmetry and precision of architectural structures.
3. Engineering Precision
Tip: Leverage the congruence of alternate interior angles to optimize the design and functionality of engineering projects.
Real life application
Scenario: Architectural Design
Architects use the concept of alternate interior angles to ensure the symmetry and balance of architectural structures, creating visually appealing and structurally sound designs.
Scenario: Engineering Precision
Engineers apply the properties of alternate interior angles to optimize the functionality and efficiency of mechanical and structural systems, ensuring precision and accuracy in their designs.
FAQ's
Alternate interior angles are a pair of angles that are formed when a transversal intersects two lines. They are located on opposite sides of the transversal and inside the two lines.
Understanding alternate interior angles is crucial in geometry as it helps in proving theorems, solving geometric problems, and determining the congruence of angles and lines.
Alternate interior angles are related in such a way that they are always congruent, meaning they have the same measure or size.
Yes, the concept of alternate interior angles can be applied in various real-life scenarios such as architecture, engineering, and design to ensure the accuracy and symmetry of structures.
The properties of alternate interior angles include being congruent, forming a ‘Z’ shape when lines are parallel, and playing a key role in the proof of theorems related to parallel lines and transversals.
Like? Share it with your friends
Facebook
Twitter
LinkedIn