How to Find the Area of a Circle: Formula and Example
Table of Contents
Introduction
Area of a Circle
The area of a circle is a fundamental concept in geometry, representing the amount of space enclosed by the circular shape. It is essential to comprehend the formula and method for calculating the area of a circle to solve mathematical problems and address real-world challenges.
Analogy of Definition
What is the Area of a Circle?
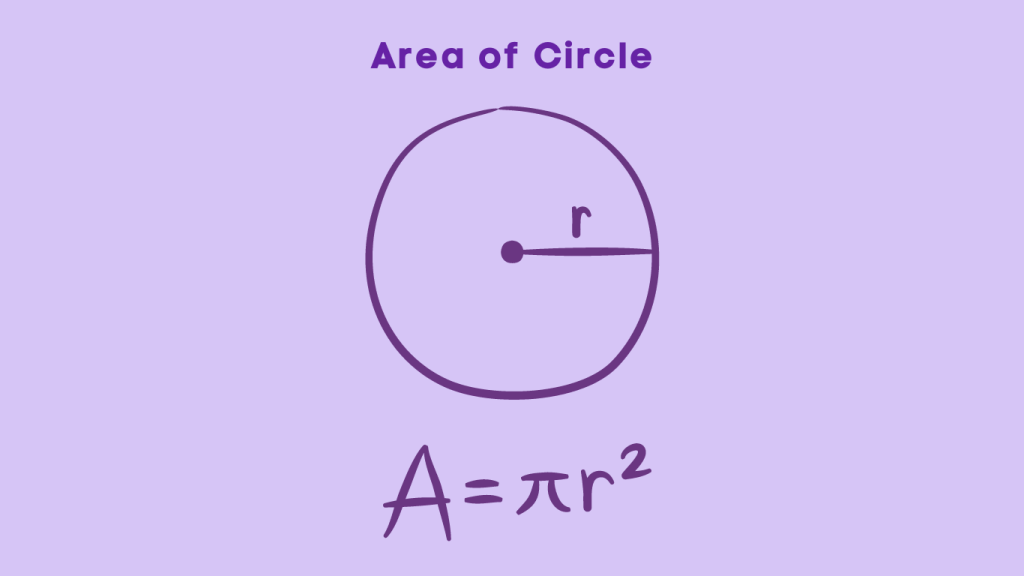
The area of a circle is defined as the total space enclosed by the boundary of the circle. It is calculated using the formula A = πr^2, where A represents the area and r is the radius of the circle.
Method
Calculating the Area of a Circle
To calculate the area of a circle, the formula A = πr² is utilized, where π is a constant approximately equal to 3.14159 and r is the radius of the circle. Substituting the value of the radius into the formula allows for the determination of the area of the circle.
Examples
Step 1: Identify the radius of the circle, which is 5 units.
Step 2: Apply the formula A = πr², substituting the value of the radius.
A = 3.14159 x (5)²
A = 3.14159 x 25
A ≈ 78.54 square units.
Thus, the area of the circle with a radius of 5 units is approximately 78.54 square units.
Summary:
This example demonstrates the process of finding the area of a circle with a radius of 5 units using the formula A = πr^2. By substituting the value of the radius into the formula, the area of the circle is calculated to be approximately 78.54 square units. This example illustrates the practical application of the area of a circle formula in determining the space enclosed by a circular shape.
This example demonstrates the process of finding the area of a circle with a radius of 5 units using the formula A = πr^2. By substituting the value of the radius into the formula, the area of the circle is calculated to be approximately 78.54 square units. This example illustrates the practical application of the area of a circle formula in determining the space enclosed by a circular shape.
Quiz
Tips and Tricks
1. Understanding the Value of π
Tip: Remember to use the value of π as approximately 3.14159 when applying the area formula.
2. Diameter to Radius
Tip: If you know the diameter 𝑑 of the circle, remember that the radius r is half of the diameter.
3. Unit Consistency
Tip: Ensure that all measurements are in the same units before calculating the area. If the radius is in meters, the area will be in square meters.
4. Half Circles
Tip: Similarly, for a semicircle, divide the area of the full circle by 2: A = (1/2) × π × r²
Real life application
Story: The Circular Construction Project
A construction team embarked on a project to build a circular structure, requiring precise calculations of the area of the circular foundation.
Challenge 1: The Circular Foundation
The construction team needed to determine the amount of concrete required to cover the circular foundation of the building. By calculating the area of the circular foundation using the formula A = πr^2, they accurately estimated the quantity of concrete needed for the project.
Challenge 2: The Circular Roof Design
In the architectural phase of the project, the design team utilized the concept of the area of a circle to calculate the surface area of the circular roof. This enabled them to optimize the use of roofing materials and ensure the structural integrity of the circular roof.
Challenge 3: The Circular Garden Landscape
The landscaping team applied the area formula to determine the space occupied by a circular garden within the construction site. This facilitated the planning and design of the garden landscape, enhancing the aesthetic appeal of the circular space.
FAQ's
The formula to find the area of a circle is A = πr^2, where A represents the area and r is the radius of the circle. The value of π is approximately 3.14159.
Calculating the area of a circle is important in various real-life applications such as construction, engineering, and design. It helps in determining the amount of material needed to cover a circular surface or to create circular structures.
The radius plays a crucial role in determining the area of a circle as it directly affects the size of the circle. The larger the radius, the greater the area of the circle.
No, the area of a circle cannot be accurately calculated without knowing the radius. The radius is an essential component of the formula for finding the area of a circle.
The concept of the area of a circle finds practical applications in various fields such as agriculture, architecture, and manufacturing. It is used to determine the space occupied by circular fields, the surface area of circular buildings, and the amount of material required to produce circular objects.
Like? Share it with your friends
Facebook
Twitter
LinkedIn