How to Find the Area of a Triangle?
Table of Contents
Introduction
Area of a Triangle
The area of a triangle is a fundamental concept in geometry, serving as the basis for calculating the surface area of triangular shapes. Let’s delve into the various formulas and methods used to determine the area of a triangle and explore its significance in practical applications.
Analogy of Definition
Triangle Area Formulas
The area of a triangle can be calculated using different formulas. Each formula provides a unique approach to finding the area of a triangle based on its measurements and angles. Here’s a table summarizing the formulas for finding the area of triangles of different types:
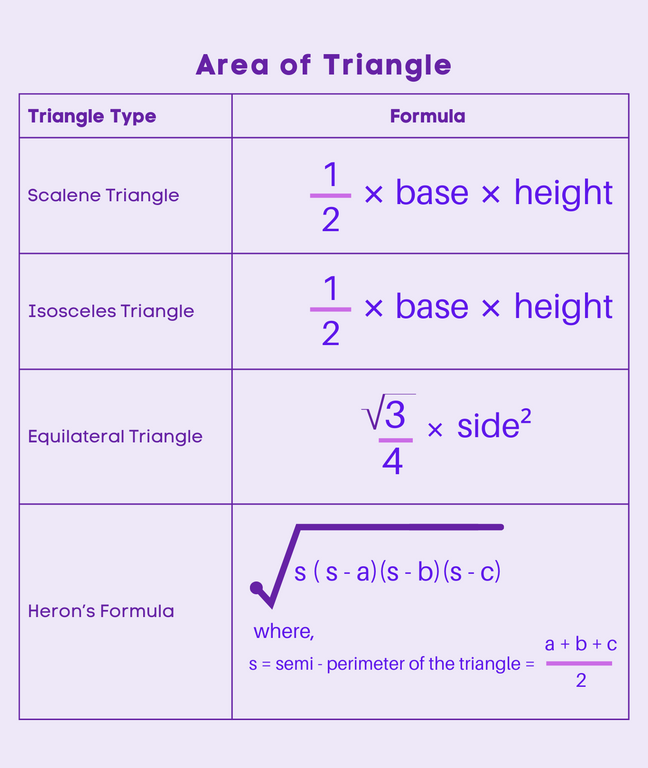
Method
Calculating the Area of a Triangle
There are multiple methods to calculate the area of a triangle, such as using the basic formula involving the base and height, and Heron’s formula, which considers all three side lengths of the triangle.
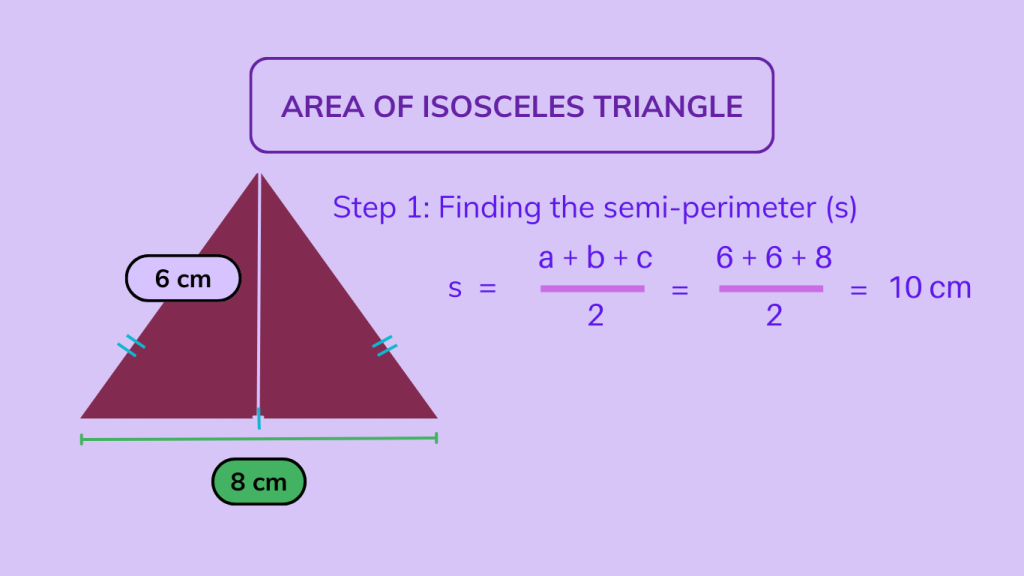
Let’s try finding out the area of a triangle using Heron’s formula.
Step 1: Find the semi-perimeter
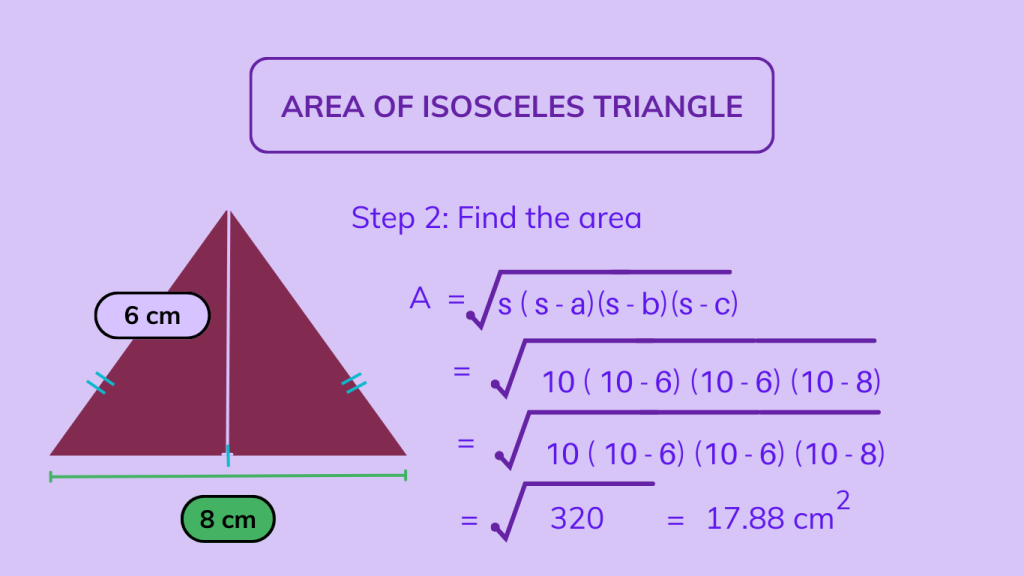
Step 2: Find the area
Examples
Example 1:
Given: Base = 6 units, Height = 4 units
Calculation: A = 1/2 × 6 × 4 = 12 square units
Result: The area of the triangle is 12 square units.
Example 2:
Given: Side lengths: 3 units, 4 units, 5 units
Calculation: Using Heron’s formula, A = √(s(s-a)(s-b)(s-c)), where s is the semi-perimeter of the triangle
Result: The area of the triangle is 6 square units.
Summary of Finding the Area of a Triangle Examples: These examples illustrate the application of different formulas and methods to find the area of a triangle. Whether using the basic formula with base and height, the trigonometric formula with side lengths and angles, or Heron’s formula with all three side lengths, each approach provides a unique way to calculate the area of a triangle based on its measurements and characteristics.
Quiz
Tips and Tricks
1. Basic Formula Tip
Tip: Utilize the formula A = 1/2 × base × height to calculate the area of the triangle.
2. Heron’s Formula Tip
Tip: Apply the formula A = √(s(s-a)(s-b)(s-c)), where s is the semi-perimeter of the triangle, to find the area.
3. Height
Tip: The height of a triangle is perpendicular to the base. If the height is not given directly, try to identify a perpendicular line from one vertex to the base.
4. Using Side Lengths
Tip: If you know the lengths of all three sides of a triangle, you can use Heron’s formula to find the area. Heron’s formula is particularly useful for triangles where the height is not easily identifiable.
Real life application
Scenario: Land Surveying
When surveying land plots, the knowledge of finding the area of a triangle is essential for accurately measuring the surface area of triangular sections of land, allowing for precise calculations of property boundaries and dimensions.
Scenario: Construction Planning
In construction planning, understanding the area of a triangle is crucial for determining the amount of material needed for triangular structures such as roofs, awnings, and support beams, ensuring efficient resource allocation and cost-effective construction.
Scenario: Art and Design
The concept of finding the area of a triangle is applied in art and design to calculate the surface area of triangular shapes, enabling artists and designers to create aesthetically pleasing compositions and geometric patterns.
FAQ's
The formula to find the area of a triangle is A = 1/2 * base * height, where A represents the area, and the base and height are the respective measurements of the triangle.
Yes, the area of a triangle can also be calculated using the Heron’s formula.
Understanding how to find the area of a triangle is crucial in various fields such as geometry, architecture, engineering, and construction, as it allows for accurate measurements and calculations of surface areas.
In addition to the basic and trigonometric formulas, the area of a triangle can also be calculated using Heron’s formula, which takes into account the lengths of all three sides of the triangle.
The concept of finding the area of a triangle finds practical applications in everyday situations such as measuring land plots, determining the amount of material needed for construction, and calculating the surface area of objects with triangular shapes.
Like? Share it with your friends
Facebook
Twitter
LinkedIn