Types of Triangles – Properties and Example
Table of Contents
Introduction
Triangles
Triangles are fundamental geometric shapes that consist of three sides and three angles. They are widely studied in mathematics and have various classifications based on their sides and angles. Let’s delve into the world of triangles and explore the different types based on their unique characteristics.
Analogy of Definition
Types of Triangles
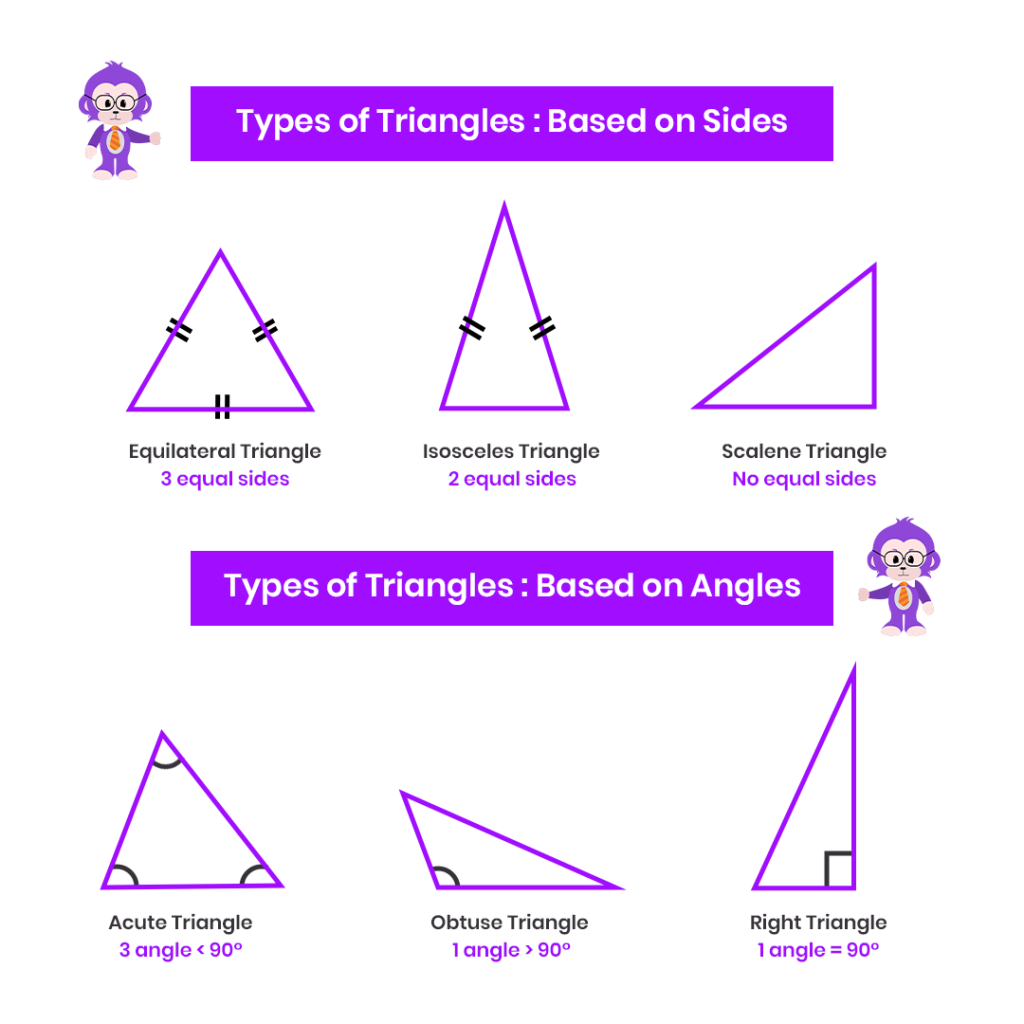
Triangles can be classified into different types based on their sides and angles. Based on sides, the types of triangles are categorized as Scalene, Isosceles, and Equilateral. Based on angles, the types of triangles are classified as Acute-angled, Obtuse-angled, and Right-angled.
Method
Types of Triangles – Based on Sides
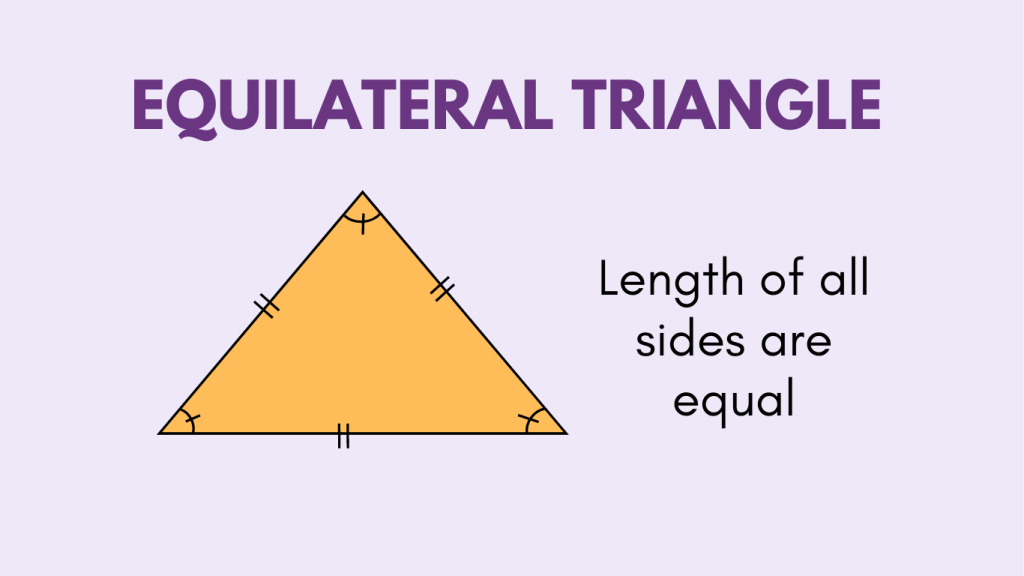
Equilateral Triangle
An equilateral triangle is type of triangle in which all three sides are of equal length. Additionally, all three angles in an equilateral triangle are congruent and measure 60 degrees. Equilateral triangles possess a high degree of symmetry and are often used in geometry and architecture.
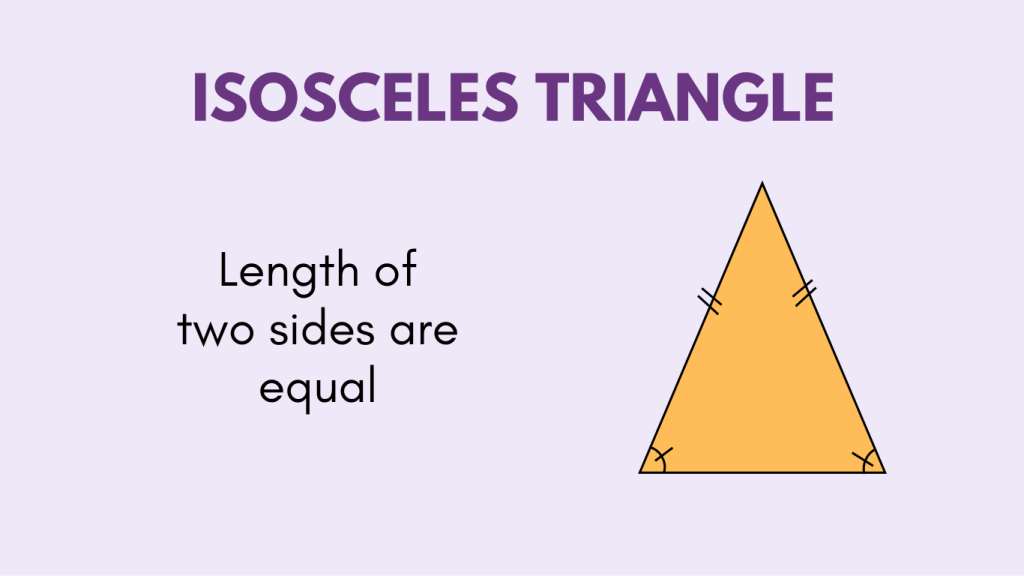
Isosceles Triangle
An isosceles triangle is a triangle with at least two sides of equal length. Consequently, the angles opposite the equal sides are also equal. Depending on the specific lengths of the sides, isosceles triangles may have one acute angle and two obtuse angles, or they may have two acute angles and one obtuse angle.
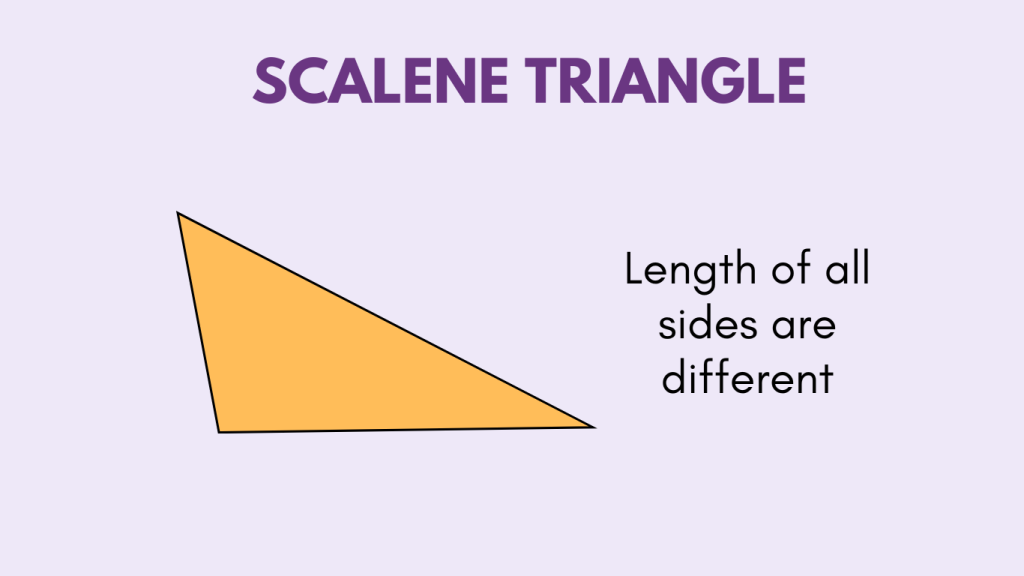
Scalene Triangle
A scalene triangle is a triangle in which all three sides have different lengths. As a result, none of the angles in a scalene triangle are equal. Scalene triangles can have a variety of angle measures, and they often require trigonometric methods to solve for their side lengths and angles.
Types of Triangles – Based on Angles
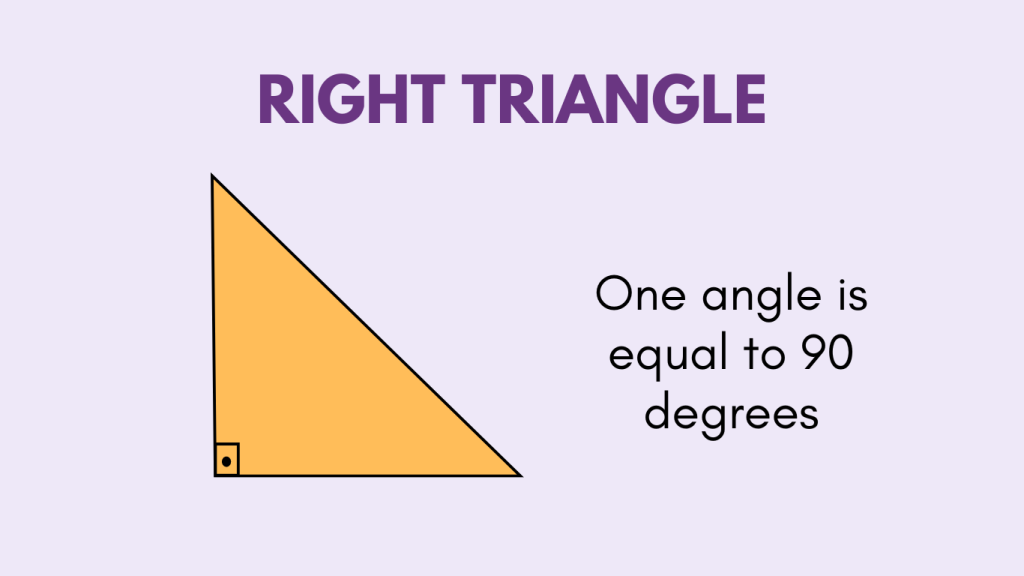
Acute Triangle
An acute triangle is a triangle in which all three angles are acute, meaning they are less than 90 degrees. Acute triangles have three acute angles and can be equilateral, isosceles, or scalene.
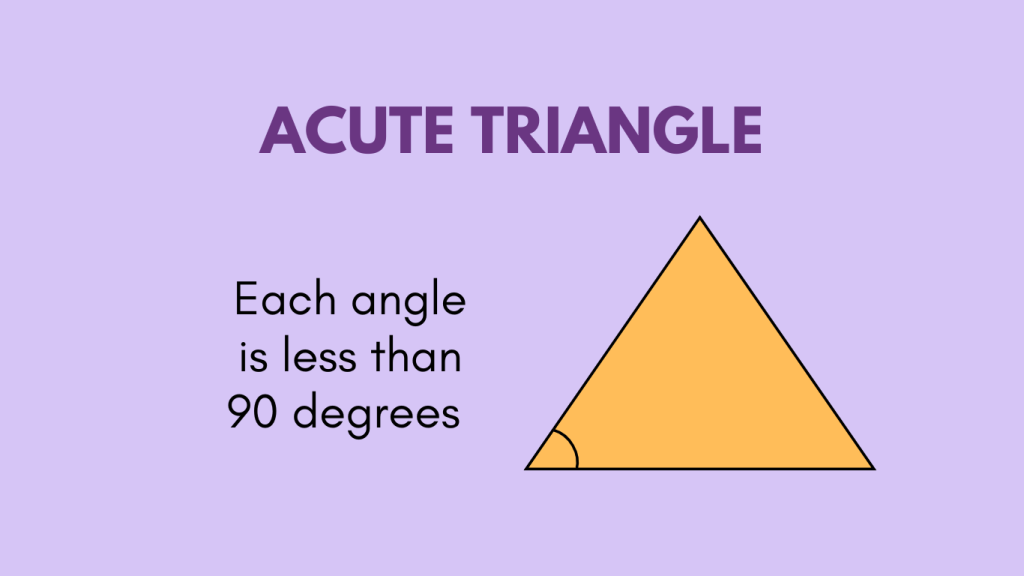
Obtuse Triangle
An obtuse triangle is a triangle in which one angle is obtuse, meaning it measures more than 90 degrees, while the other two angles are acute. Obtuse triangles can be isosceles or scalene but cannot be equilateral since all angles in an equilateral triangle are 60 degrees.
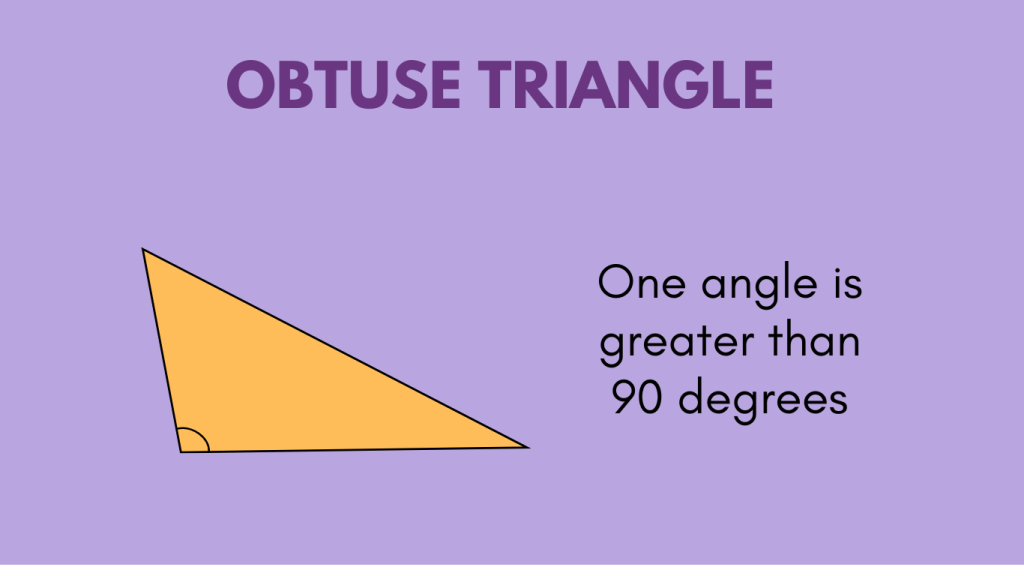
Right Triangle
A right triangle is a triangle in which one angle is a right angle, measuring exactly 90 degrees. The side opposite the right angle is called the hypotenuse, and the other two sides are called legs. Right triangles play a significant role in trigonometry, and they are commonly used in various fields such as engineering, physics, and construction.
Examples
Identifying Types of Triangles
Example 1: Scalene Triangle
A triangle with sides of different lengths, such as 3 cm, 4 cm, and 5 cm, is classified as a Scalene triangle.
Example 2: Isosceles Triangle
A triangle with two sides of equal length and one side of a different length, such as 5 cm, 5 cm, and 7 cm, is classified as an Isosceles triangle.
Example 3: Equilateral Triangle
A triangle with all three sides of equal length, such as 6 cm, 6 cm, and 6 cm, is classified as an Equilateral triangle.
Quiz
Tips and Tricks
1. Scalene Triangle
Tip: A Scalene triangle has all sides of different lengths. It does not have any equal sides or angles.
2. Isosceles Triangle
Tip: An Isosceles triangle has two sides of equal length and two equal angles opposite those sides.
3. Equilateral Triangle
Tip: An Equilateral triangle has all three sides of equal length and all three angles are equal, each measuring 60 degrees.
4. Acute-angled Triangle
Tip: An Acute-angled triangle has all three angles measuring less than 90 degrees.
5. Obtuse-angled Triangle
Tip: An Obtuse-angled triangle has one angle measuring more than 90 degrees.
Real life application
Scenario 1: Construction
In construction, knowledge of different types of triangles is essential for designing and building structures with precise angles and measurements.
Scenario 2: Art and Design
Artists and designers use the concept of different types of triangles to create visually appealing compositions and geometric patterns.
Scenario 3: Navigation
In navigation and map reading, understanding different types of triangles is crucial for determining distances and directions.
FAQ's
A Scalene triangle is a triangle with all sides of different lengths and no equal angles.
An Isosceles triangle has two sides of equal length and two equal angles opposite those sides.
An Equilateral triangle has all three sides of equal length and all three angles are equal, each measuring 60 degrees.
An Acute-angled triangle has all three angles measuring less than 90 degrees.
An Obtuse-angled triangle has one angle measuring more than 90 degrees, making it the largest angle in the triangle.
Like? Share it with your friends
Facebook
Twitter
LinkedIn