Understanding Circumference to Diameter Conversion and Formula
Table of Contents
Introduction
Circumference and Diameter
The relationship between the circumference and diameter of a circle is a fundamental concept in geometry and mathematics. Let’s delve into the intricacies of this relationship and explore the significance of understanding the conversion formula.
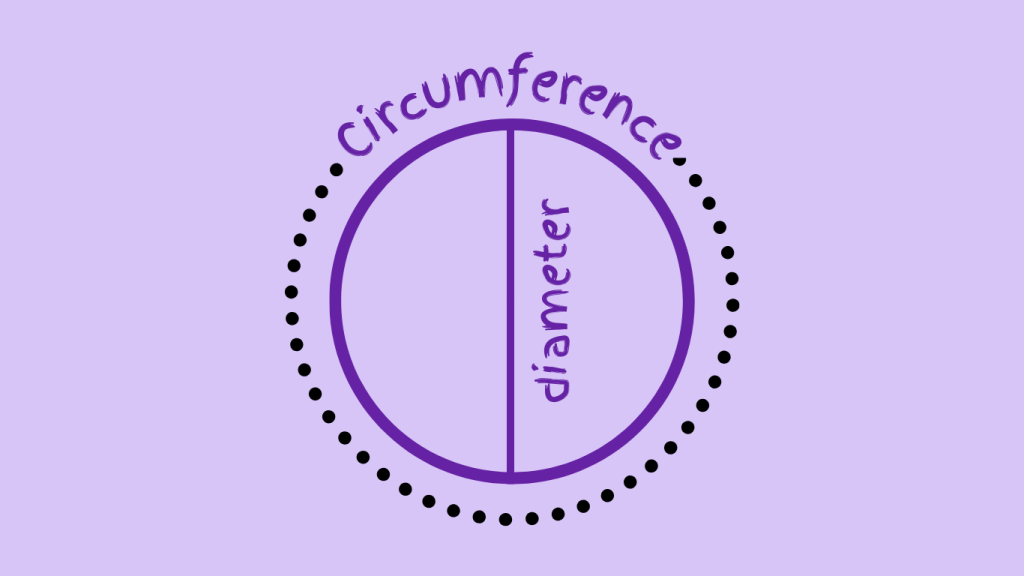
Analogy of Definition
How are Circumference and Diameter Related?
The circumference of a circle is the distance around its outer boundary, while the diameter is the distance across the circle through its center. The relationship between the two is encapsulated by the formula C = πd, where C represents the circumference, d represents the diameter, and π is the constant ratio.
Method
Converting Circumference to Diameter
To convert the circumference to diameter, the formula C = πd is utilized, where the circumference is divided by pi to obtain the diameter. Conversely, to convert the diameter to circumference, the formula d = C / π is employed, where the diameter is multiplied by pi to determine the circumference.
Examples
Given: Circumference (C) = 12π units
Calculation: Using the formula C = πd, we can solve for the diameter (d) by dividing the circumference by π.
d = C / π = 12π / π = 12 units
Result: The diameter of the circle is 12 units.
Summary:
This example illustrates the process of converting the circumference of a circle, given as 12π units, to its corresponding diameter. By applying the formula C = πd and performing the necessary calculations, the diameter of the circle is determined to be 12 units. This demonstrates the practical application of the circumference to diameter conversion formula in solving real-world problems.
This example illustrates the process of converting the circumference of a circle, given as 12π units, to its corresponding diameter. By applying the formula C = πd and performing the necessary calculations, the diameter of the circle is determined to be 12 units. This demonstrates the practical application of the circumference to diameter conversion formula in solving real-world problems.
Quiz
Tips and Tricks
1. Practical Application in Construction:
Scenario: Calculating the diameter of a circular foundation.
Tip: Utilize the formula C = πd to convert the known circumference of the foundation to its diameter for accurate construction planning and execution.
2. Precision in Manufacturing:
Scenario: Determining the circumference of a circular component.
Tip: Apply the formula d = C / π to convert the known diameter of the component to its circumference, ensuring precise measurements and quality control.
3. Designing Circular Structures:
Scenario: Planning the layout of a circular garden.
Tip: Use the relationship between circumference and diameter to calculate the required dimensions and proportions for the circular design, enhancing aesthetic appeal and functionality.
Real life application
Real-Life Applications of Circumference to Diameter Conversion:
Story: The Architect’s Challenge
An architect faced the challenge of designing a circular courtyard with a specified circumference. By applying the concept of circumference to diameter conversion, the architect was able to calculate the required diameter for the courtyard, ensuring precise construction and harmonious integration with the surrounding architecture.
Challenge 1: The Construction Conundrum
A construction team needed to determine the diameter of a circular foundation based on the given circumference to ensure accurate placement and structural stability. By employing the formula C = πd, the team successfully converted the circumference to the required diameter, facilitating seamless construction.
Challenge 2: The Manufacturing Mystery
In a manufacturing facility, engineers needed to calculate the circumference of a circular component to verify its dimensions. Utilizing the formula d = C / π, they converted the known diameter to the precise circumference, ensuring quality control and adherence to specifications.
Challenge 3: The Design Dilemma
A landscape designer sought to create a circular garden with a specific circumference, requiring the calculation of the corresponding diameter. By understanding the relationship between circumference and diameter, the designer achieved a harmonious layout and aesthetic balance within the garden.
FAQ's
The relationship between circumference and diameter is defined by the mathematical constant pi (π). The circumference of a circle is directly proportional to its diameter, with the value of pi representing the ratio of the circumference to the diameter.
The circumference to diameter conversion formula is expressed as C = πd, where C represents the circumference, d represents the diameter, and π is the constant approximately equal to 3.14159.
Yes, the diameter to circumference conversion formula can be derived from the circumference to diameter formula by rearranging the equation to solve for the diameter, resulting in the formula d = C / π.
Understanding the relationship between circumference and diameter is crucial in various fields such as engineering, architecture, and mathematics, as it enables accurate calculations and measurements related to circular objects and structures.
The concept of circumference to diameter conversion finds practical applications in fields such as construction, manufacturing, and design, where precise measurements and calculations related to circular shapes are essential for achieving optimal results.
Like? Share it with your friends
Facebook
Twitter
LinkedIn