Descending Order – Meaning, Symbols and Examples
Table of Contents
Introduction
Descending Order
In the realm of mathematics, the concept of descending order plays a crucial role in organizing and comparing numbers. Whether it’s integers, decimals, or fractions, understanding how to arrange numbers in descending order is essential for various mathematical operations. Let’s delve into the world of descending order and explore its significance in mathematical contexts.
Analogy of Definition
What is Descending Order?
Descending order is a mathematical arrangement of numbers in decreasing magnitude, from the smallest value to the largest value. Descending order is represented by the greater than symbol “>” and is used to arrange numbers from the largest to the smallest. When arranging numbers in descending order, the largest number appears first, followed by the next largest, and so on, until the smallest number is listed last. By understanding the concept of descending order, we can know which number is larger and which is smaller.
Method
Arranging Integers in Descending Order
To arrange integers in descending order, start by comparing the numbers and placing the largest number first, followed by the next largest, and so on. This process continues until all the numbers are arranged in descending order.
Positive Integers in Descending Order
Arranging positive integers in descending order involves considering their magnitude and place values. Here’s how it works:
- Magnitude Comparison: Begin by comparing the magnitude of the integers. When comparing the magnitude of integers, the larger the magnitude, the farther the integer is from zero on the number line.
- Place Value Consideration: If two positive integers have the same magnitude, compare their place values. The integer with more and higher digits is larger, while the one with fewer and lowerdigits is smaller.
- Iterative Comparison: Continue comparing the magnitude and place values of each integer until they are arranged from the largest to the smallest.
For example: Given positive integers: 872, 431, 596, 1239
- 1239 has the largest magnitude.
- Among the three-digit numbers, 596 is larger than 431.
- Finally, comparing 872 and 431, 872 is larger.
Thus, the descending order is: 1239 > 872 > 596 > 431.

Negative Integers in Descending Order
Organizing negative integers in descending order involves understanding their behavior on the number line. Here’s how it’s done:
- Magnitude Comparison: Just like with positive integers, begin by comparing the magnitude of the negative integers. The larger the magnitude of a negative integer, the farther it is from zero on the number line, and therefore, the smaller it is in terms of magnitude.
- Application of Negativity: Remember that a smaller negative integer (-a) is positioned to the right of a larger negative integer (-b) on the number line.
- Iterative Comparison: Continue comparing the magnitude of each negative integer until they are arranged from the largest to the smallest.
For instance: Given negative integers: -29, -87, -54, -112
- Comparing magnitude, -29 has the largest.
- Among the two-digit numbers, -87 is smaller than -54.
- Finally, comparing -54 and -112, -54 is larger.
Thus, the descending order is: -29 > -54 > -87 > -112.
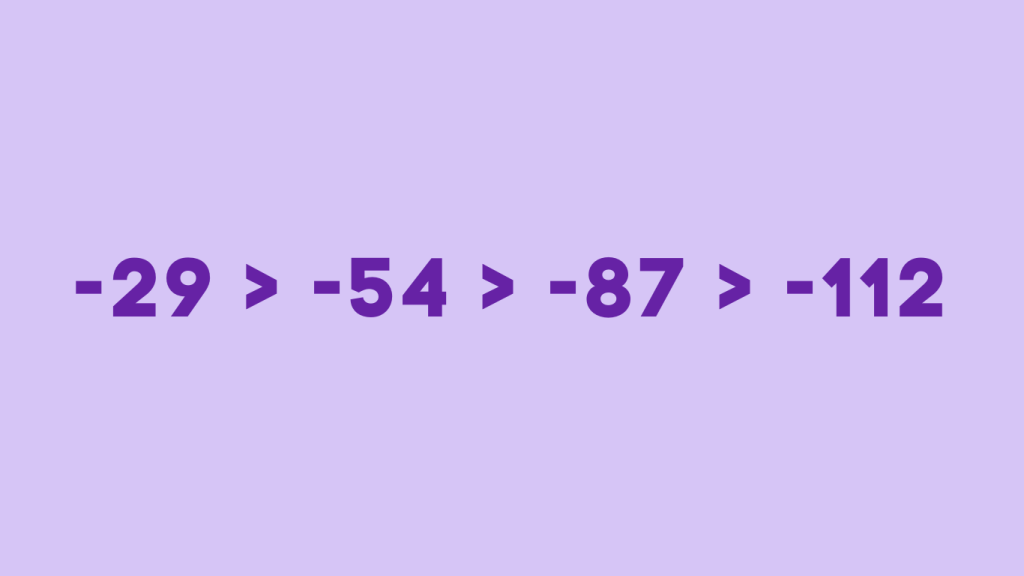
Descending Order on a Number Line
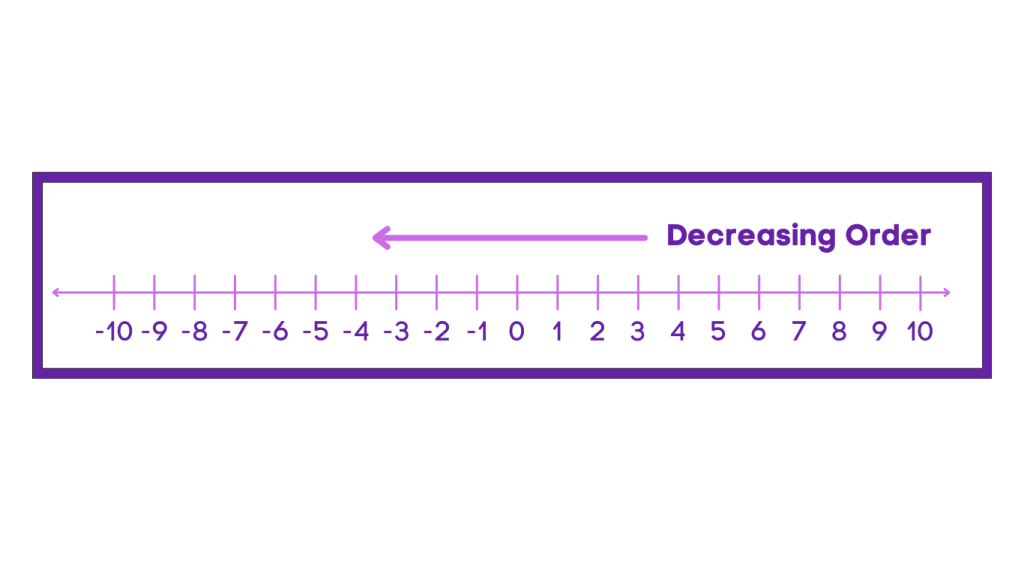
Another method for arranging numbers in descending order involves using a number line. By plotting the numbers on a number line and identifying the largest and smallest values, you can visualize the descending order of the numbers. In a number line, digits decrease as we move from right towards the left. So the order in the number line is in decreasing form as we look from right to left.
Descending Order for Fractions
When dealing with decimals and fractions, the process of arranging numbers in descending order follows the same principles as with integers. Compare the values and place them in descending order, ensuring that the largest value appears first and the smallest value appears last. The method of ordering like fractions and unliked fraction differs slightly. Let’s see how we can arrange fractions in decreasing order.
Descending Order for Like fractions
The fractions whose denominator are same are known as like fractions. Such fractions can be put in descending order by comparing the numerators.
For example: Arranging the fractions \frac{4}{2}, \frac{5}{2}, \frac{7}{2}, \frac{8}{2}
Let’s arrange the numerators in descending order, 8 > 7 > 5 > 4, which will be \frac{8}{2}, \frac{7}{2}, \frac{5}{2}, \frac{4}{2}
Descending Order for Unlike Fractions
The fractions with diferent denominators are known as unlike fractions. To arrange such fractions in descending order, we will have to convert them into like fractions by finding out the LCM of the denominators. Then, we will compare the numerators to arrange in desceding order.
For example: Arranging the fractions \frac{1}{5}, \frac{4}{2}, \frac{3}{6}, \frac{5}{3}
Step 1: We need to find the LCM of the numbers 2, 3, 5 and 6, which is 30.
Step 2: Converting the fractions to like we get \frac{6}{30}, \frac{60}{30}, \frac{15}{30}, \frac{50}{30}
Step 3:We will then arrange the numerator in descending order 60 > 50 > 15 > 6
Step 4: Now will we put the numbers in their fraction forms, which will give us \frac{60}{30}, \frac{50}{30}, \frac{15}{30}, \frac{6}{30}
When arranging decimals in descending order, you compare the place values to determine the order from the smallest to the largest decimal. We begin from checking from the left-most digit and if they match we move to the next digit, and if one digit is greater than the other in the same place value, we know that the number is greater.
Descending Order for Decimals
Decimals are a way to represent parts of a whole, dividing something into smaller pieces, like dividing a dollar into cents. They’re like tiny fractions that make counting and measuring more precise. When arranging decimals in descending order, you compare the place values to determine the order from the largest to the small decimal. We begin from checking from the left-most digit and if they match we move to the next digit, and if one digit is less than the other in the same place value, we know that the number is lower.
Arranging 1.34, 2.32, 1.15,3.42
Step 1: Comparing the left-most digit, 3 is the greatest one, so 3. 42 is the highest number
Step 2: Comparing the next digit, 2 is the second largest one, so 2.32 is the second highest number.
Step 3: After 2, we have two numbers beginning with 1, so we will check the next digit, 1.34 has 3 in the tenths place and in 1.15, we have 1 in the tenth place, so 1.34 is greater than 1.15
Step 4: Hence, the numbers in descending order will be 3.42 > 2.32 > 1.34 > 1.15
Examples
Example 1: Arranging the numbers 25, 17, 39, and 12 in descending order.
We can arrange the numbers in Descending order as 39, 25, 17, 12
Example 2: Arranging the decimals 3.6, 2.9, 4.2, and 1.8 in descending order.
We can arrange the numbers in Descending order as 4.2, 3.6, 2.9, 1.8
Quiz
Tips and Tricks
1. Start with the Largest Number
Tip: Begin by identifying the largest number in the set. This will be the first number in the descending order sequence.
2.Compare Numbers
Tip: Compare each remaining number to the largest number you’ve identified. Place the next largest number next in the sequence.
3.Repeat the Process
Tip: Continue comparing the remaining numbers to those already placed in the sequence. Place them accordingly, from largest to smallest.
4.Use Visual Aids
Tip: If you’re arranging a list of numbers, consider using visual aids like a number line or grid to help you visualize the order.
5. Chunking
Tip: Break the list of numbers into smaller groups and arrange each group in descending order before combining them back together.
Real life application
Scenario: “Organizing Inventory”
In a warehouse, items are often organized in descending order based on their sizes or quantities. This allows for efficient inventory management and easy access to items when needed.
Scenario: “Ranking Scores”
In sports competitions or academic assessments, scores are often ranked in descending order to identify the highest achievers or performers.
Scenario: “Financial Planning”
When prioritizing expenses or investments, individuals may arrange their financial obligations in descending order to address the most critical needs first.
FAQ's
Like? Share it with your friends

