Understanding the Equilateral Triangle: Definition, Properties, Area, and Formula
Table of Contents
Introduction
Equilateral Triangle
In the realm of geometry, the equilateral triangle holds a significant place due to its unique properties and applications. Let’s delve into the world of equilateral triangles and explore their definition, properties, area calculation, and real-life examples.
Analogy of Definition
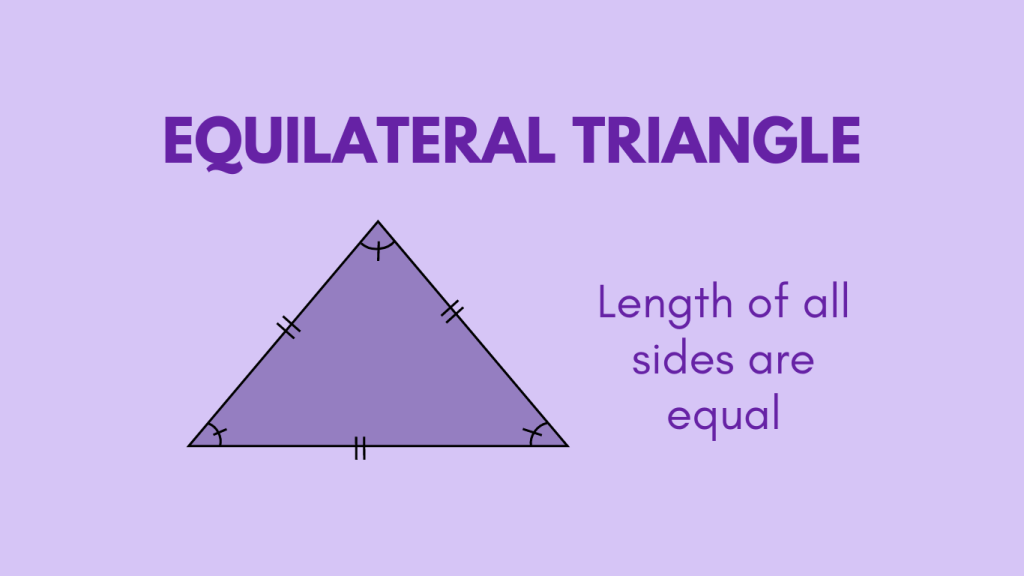
What is an Equilateral Triangle?
An equilateral triangle is a specific type of triangle characterized by the equality of all three sides. This results in the internal angles also being equal, each measuring 60 degrees. In essence, it is a triangle with three congruent sides and three congruent angles, making it different from other types of triangles.
Method
Properties of Equilateral Triangle
Equal Side Lengths: The most defining property of an equilateral triangle is that all three sides have the same length. This uniformity in side lengths ensures symmetry in the triangle’s shape, with each side contributing equally to its appearance.
Equal Interior Angles: In an equilateral triangle, all three interior angles are congruent, meaning they have the same measure. Each angle measures 60 degrees, resulting in a total angle sum of 180 degrees.
Symmetry: Due to the equal side lengths and angle measures, equilateral triangles exhibit a high degree of symmetry. They can be rotated, reflected, or translated without altering their appearance, making them visually pleasing and geometrically elegant.
Equilateral Triangle Theorem: The perpendicular bisectors of the sides of an equilateral triangle intersect at a single point known as the circumcenter. This point is equidistant from the vertices of the triangle, forming the center of the triangle’s circumcircle.
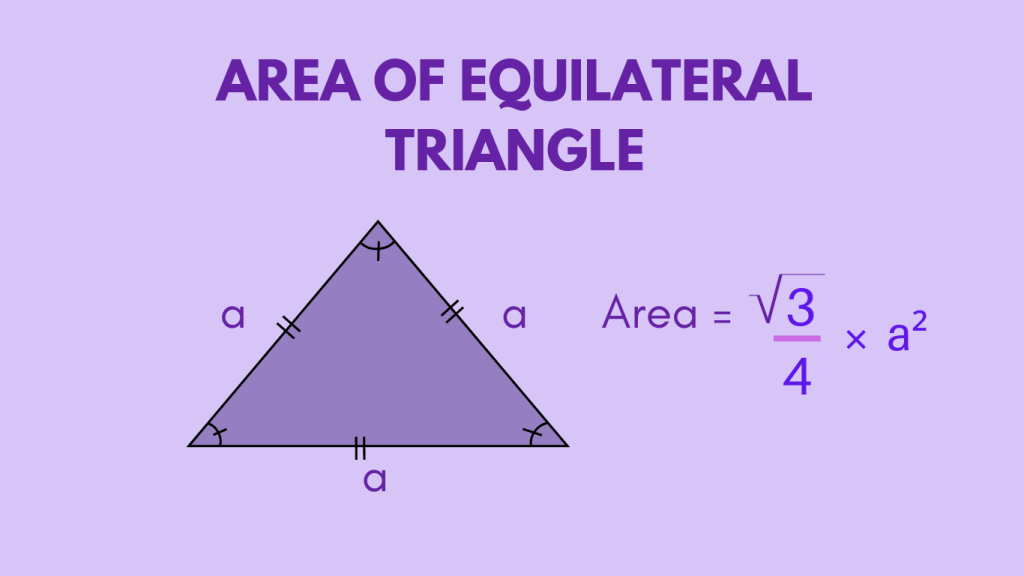
Area of an Equilateral Triangle
Examples
Example 1: Given side length = 6 units, find the area of the equilateral triangle.
Summary:
These examples illustrate the process of calculating the area of an equilateral triangle using the given side lengths. By applying the area formula, the area of the equilateral triangle can be determined, showcasing the practical application of the area formula in solving real-world problems.
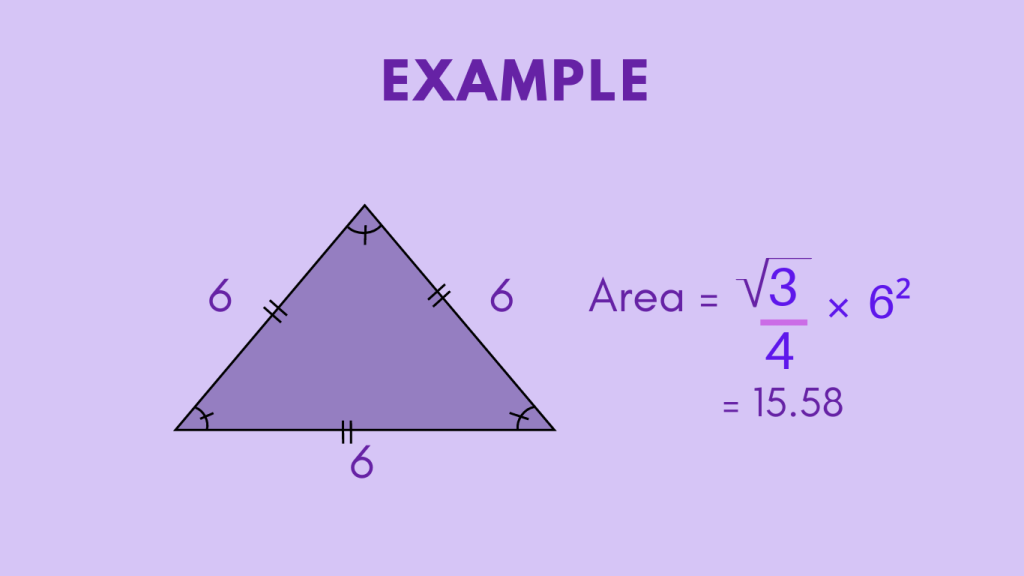
These examples illustrate the process of calculating the area of an equilateral triangle using the given side lengths. By applying the area formula, the area of the equilateral triangle can be determined, showcasing the practical application of the area formula in solving real-world problems.
Quiz
Tips and Tricks
1. Side Lengths
Tip: In an equilateral triangle, all three sides are of equal length. So if you know the length of one side, you automatically know the lengths of the other two sides.
2. Angles
Tip: Each angle in an equilateral triangle measures 60 degrees. This is because all three angles in any triangle always add up to 180 degrees, and since all angles are equal in an equilateral triangle, each angle must be 180 divided by 3, which equals 60 degrees.
3. Altitude and Median
Tip: In an equilateral triangle, the altitude (perpendicular from one vertex to the opposite side) and the median (line from one vertex to the midpoint of the opposite side) are the same line. That means, in an equilateral triangle, the altitude, median, and side are the same line segment.
4. Centroid: The centroid of an equilateral triangle (the point where all three medians intersect) divides each median into segments in a 2:1 ratio. This means that the distance from any vertex to the centroid is two-thirds the length of the median.
Real life application
Story: The Architect’s Challenge
An architect faced the challenge of designing a unique structure with equal side lengths and angles. By utilizing the properties of an equilateral triangle, the architect successfully created a blueprint for a stunning architectural marvel.
Challenge 1: The Yield Sign Puzzle
A group of students encountered a yield sign and recognized it as an example of an equilateral triangle in real life. This realization sparked their curiosity about the practical applications of equilateral triangles in everyday objects and structures.
Challenge 2: Crystallography Exploration
A team of scientists explored crystal formations and identified the presence of equilateral triangles in certain crystal structures. This discovery enhanced their understanding of geometric shapes in nature and their significance in scientific research.
Challenge 3: Architectural Marvels
An architectural firm designed a futuristic building with an equilateral triangle-shaped facade, showcasing the aesthetic appeal and structural stability of equilateral triangles in modern architecture.
FAQ's
An equilateral triangle is a type of triangle in which all three sides are of equal length. This means that all three angles of an equilateral triangle are also equal, each measuring 60 degrees.
The properties of an equilateral triangle include equal side lengths, equal internal angles of 60 degrees, and the property that it is also an equiangular triangle.
The area of an equilateral triangle can be calculated using the formula: Area = (sqrt(3) / 4) * side length squared.
The perimeter of an equilateral triangle is calculated by adding the lengths of all three sides together.
Real-life examples of equilateral triangles include the shape of a yield sign, the structure of some architectural designs, and the formation of certain crystals.
Like? Share it with your friends
Facebook
Twitter
LinkedIn