Exterior Angles of Triangle: Theorem and Properties
Table of Contents
Introduction
Exterior Angles of Triangle
The exterior angle of a triangle is an important concept in geometry with several useful properties and applications.
Analogy of Definition
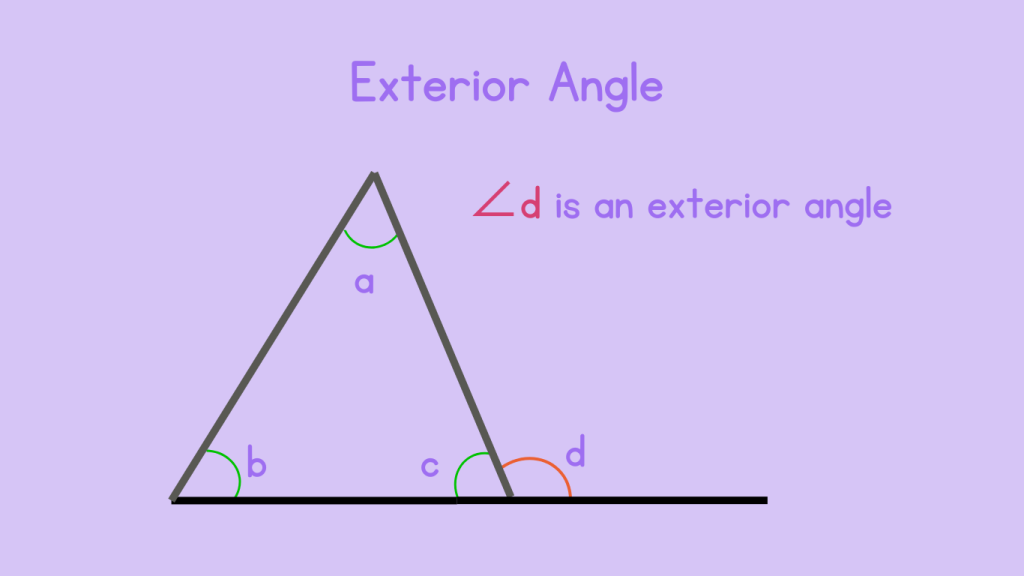
What are Exterior Angles of Triangle?
An exterior angle is formed when one side of a triangle is extended outwards. The key property of an exterior angle is that it is equal to the sum of the two non-adjacent interior angles of the triangle.
Method
Exterior Angle Theorem
The exterior angle theorem is a fundamental concept in geometry that relates the measures of exterior angles to the measures of remote interior angles in a triangle.
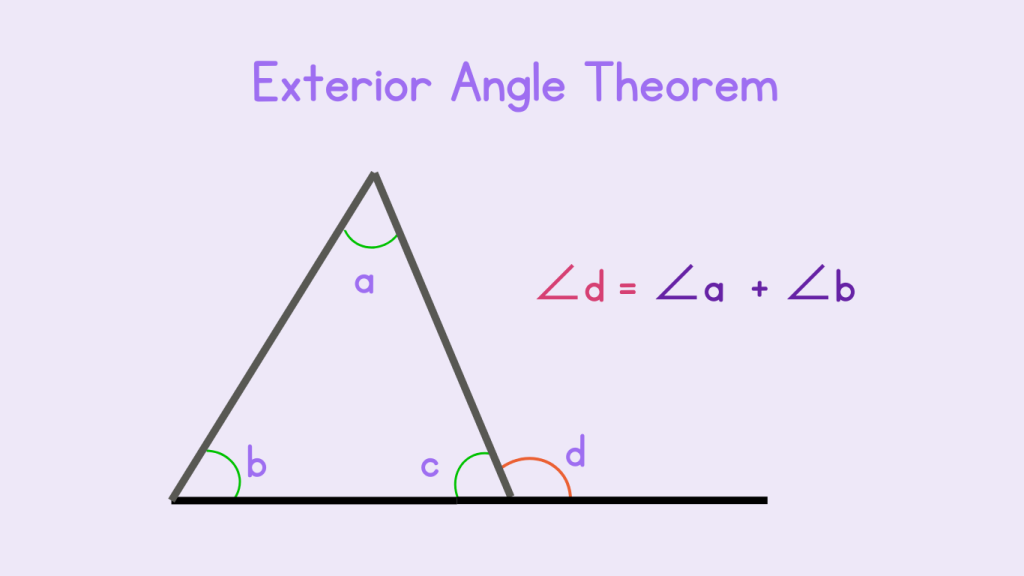
We can verify the theorem by utilising the triangle sum theorem.
As we know,
a + b + c = 180°
c = 180° – (a + b) — eq i
c + d = 180° (linear pair of angles)
d = 180° – c — eq ii
Replacing c in eq ii by eq i
d = 180° – 180°+ (a + b)
d = a + b
Hence, in this way we can verify the exterior angle theorem.
Examples
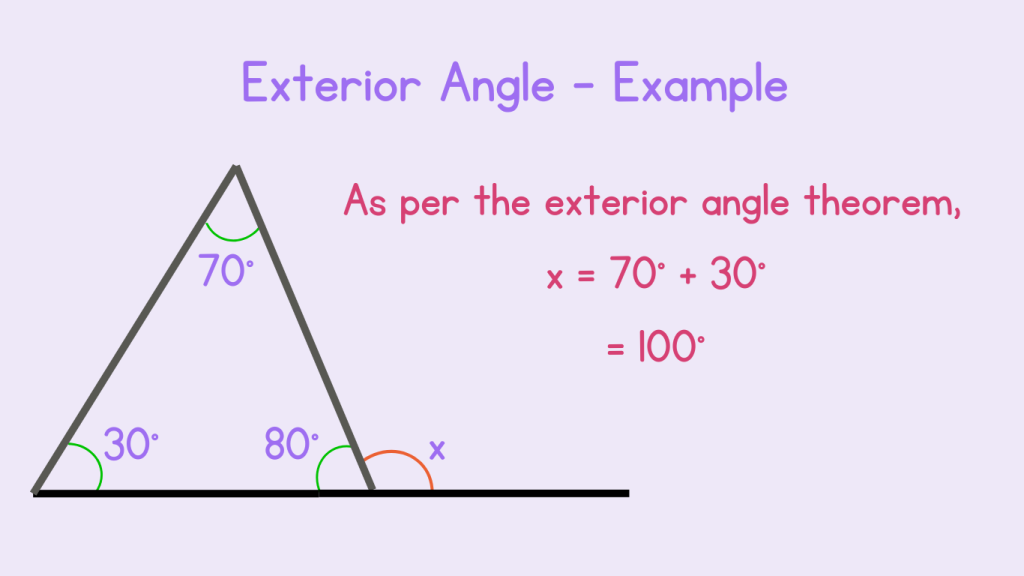
Example 1: Find the measure of x.
Quiz
Tips and Tricks
1. Remember the Exterior Angle Theorem
Tip: The measure of an exterior angle of a triangle is equal to the sum of the measures of the two non-adjacent interior angles. This is a fundamental property that can help you quickly find unknown angles.
2. Sum of Exterior Angles
Tip: The sum of the exterior angles of any polygon, including a triangle, is always 360 degrees. This property can help in checking your work and solving complex problems.
3. Using Supplementary Angles
Tip: Each exterior angle forms a linear pair with its adjacent interior angle. Since they form a straight line, they are supplementary and their measures add up to 180 degrees. If you know one angle, you can easily find the other.
4. Quick Calculation
Tip: To find the measure of an exterior angle when given the interior angles, use the Exterior Angle Theorem. For example, if the interior angles are 30 degrees and 40 degrees, the exterior angle is 30 + 40 = 70 degrees.
5. Identify Key Relationships
Tip: In a triangle, if you know two angles, you can always find the third using the fact that the sum of the interior angles is 180 degrees. This helps in finding the exterior angles as well.
Real life application
Scenario: Architectural Design
In architectural design, understanding the angles formed by the exterior sides of buildings and structures is crucial for ensuring stability and aesthetic appeal. Architects and engineers utilize the concept of exterior angles to create structurally sound and visually appealing designs.
Scenario: Construction and Engineering
In construction and engineering, the knowledge of exterior angles is essential for accurately measuring and constructing various structures, including bridges, buildings, and roadways. The precise calculation and placement of exterior angles contribute to the stability and functionality of these structures.
FAQ's
Exterior angles are the angles formed between one side of a polygon and the extension of an adjacent side. They are located outside the polygon.
The exterior angle theorem states that the measure of an exterior angle of a triangle is equal to the sum of the measures of its remote interior angles.
Alternate exterior angles are a pair of angles formed when a transversal intersects two lines. They are located on opposite sides of the transversal and are congruent.
The properties of exterior angles include the fact that the sum of all exterior angles of a polygon is always 360 degrees, and the measure of each exterior angle of a regular polygon is constant.
Exterior angles find practical applications in architecture, construction, and engineering, where understanding the angles formed by the sides of structures is essential for design and stability.
Like? Share it with your friends
Facebook
Twitter
LinkedIn
