Triangle Sum Theorem – Properties and Examples

Introduction

Triangle Sum Theorem

The Triangle Sum Theorem is a fundamental concept in geometry that establishes a relationship between the interior angles of a triangle. By exploring its properties and applications, we can gain a deeper understanding of the geometric principles governing triangles.

Analogy of Definition

What is the Triangle Sum Theorem?

The Triangle Sum Theorem states that the sum of the interior angles of a triangle is constant and equal to 180 degrees. This fundamental property holds true for all triangles, regardless of their size or shape.

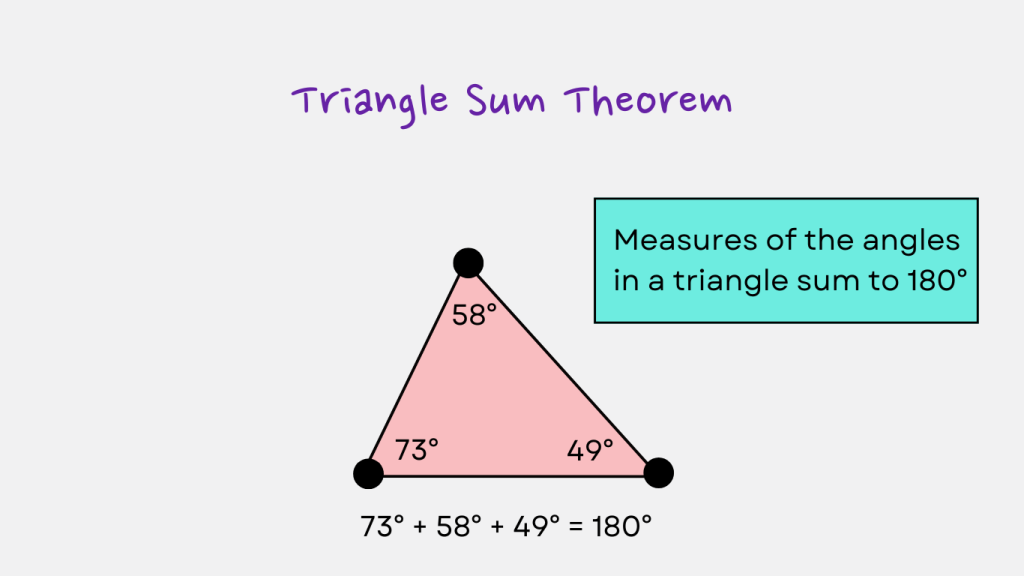
Method

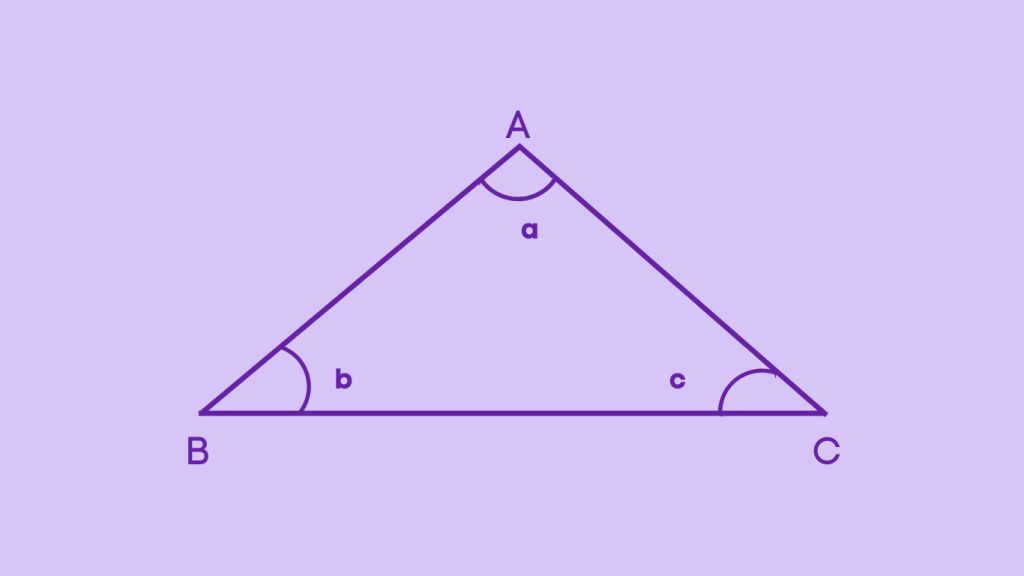
Proof of the Triangle Sum Theorem

Consider a triangle $A BC$ with vertices $A$ , $B$ , and $C$ . Let $∠a$ , $∠b$ , and $∠c$ be the interior angles of the triangle.

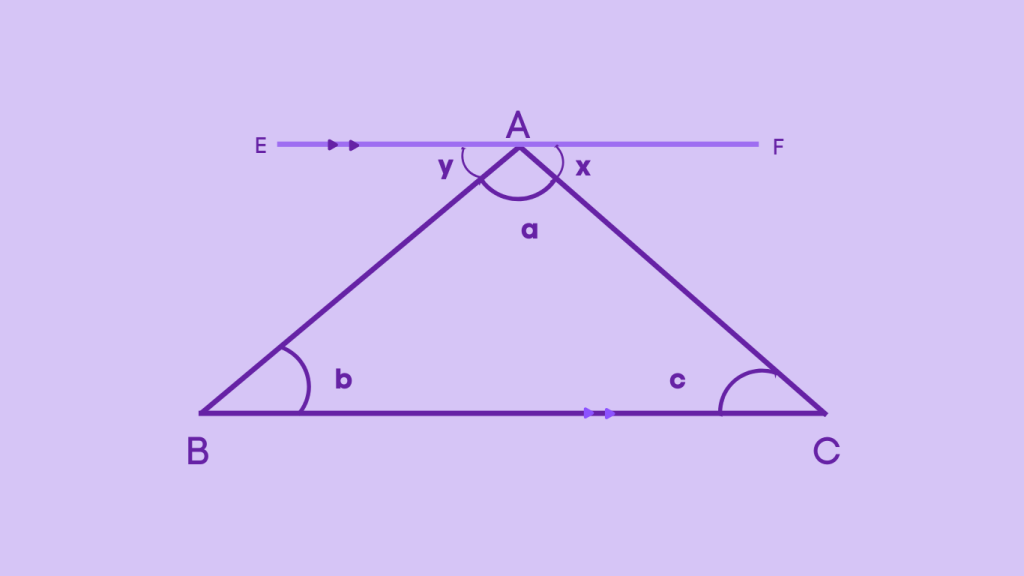
Draw a straight line EF through point B parallel to side AC, as shown in the figure below, forming $∠$ x and $∠$ y.

Line AB is a transversal for $parallel lines$ BC and EF, so $∠y = ∠b as they form an alternate angle. In the same way, Line AC is tranversal for the parallel lines BC and EF, SO ∠x = ∠c.$

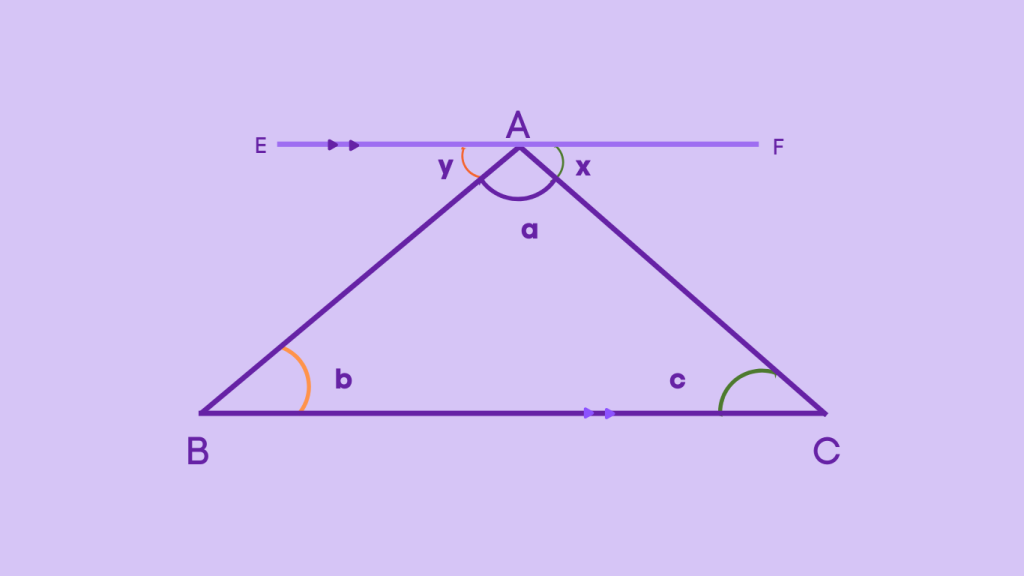
As $∠x, ∠a, and ∠y are on a straight line, ∠x +∠a + ∠y = 180°. Since, ∠x = ∠c and ∠y = ∠b, we can also write it as ∠a + ∠b + ∠c = 180°$

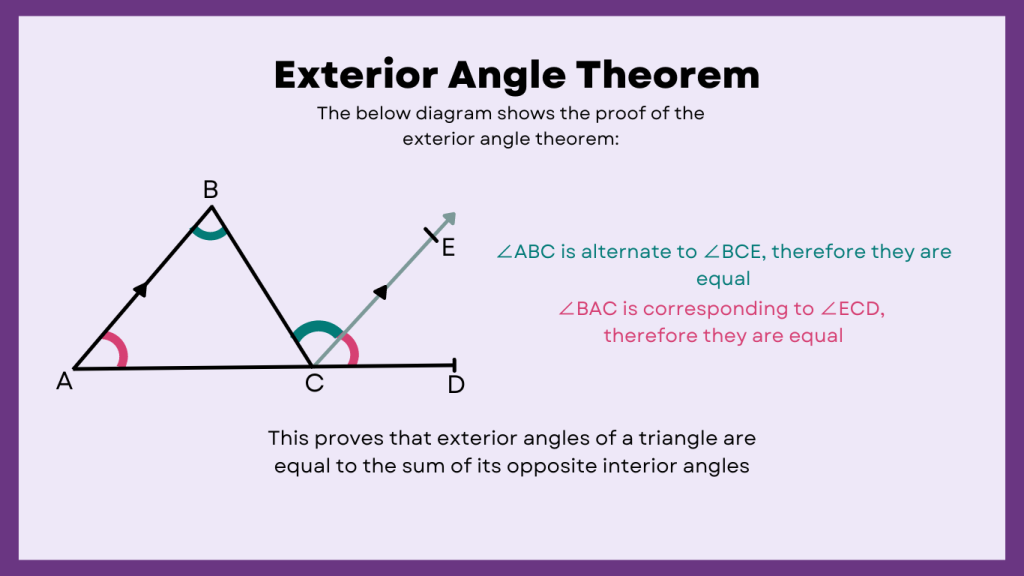
Exterior Angle Sum Theory

The Exterior Angle Sum Theorem states that the measure of an exterior angle of a triangle is equal to the sum of the measures of its two opposite interior angles.

Examples

Example 1: Finding the Third Angle of a Triangle

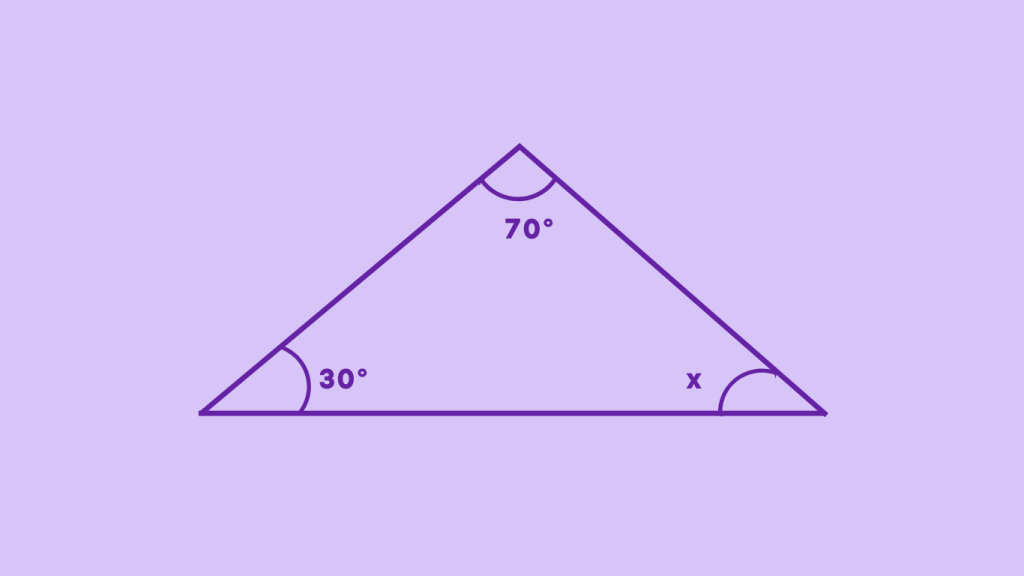
The triangle sum theory states that the sum of all three angles of a triangle is equal to 180°. Since, 70° and 30° make 100°, $∠x must be 80°.$

Example 2: Finding the Exterior Angle

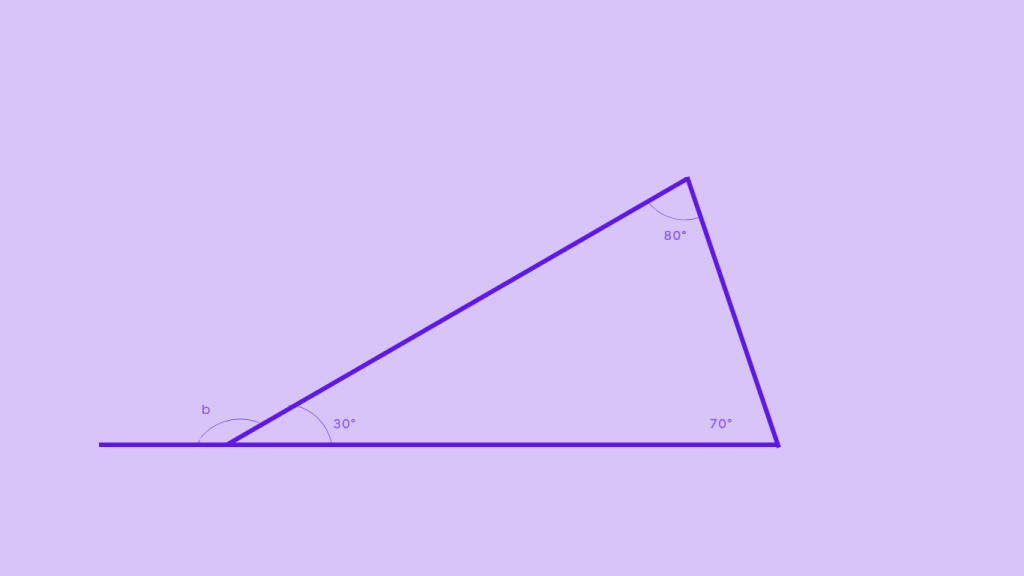
The exterior angle sum statest hat the exterior angle is equal to the sum of two opposite interior angles of a triangle. S0, $∠b = 80° + 70° = 130°$

Summary:
This example demonstrates the application of the Triangle Sum Theorem to find the measure of the third angle in a triangle. By leveraging the theorem’s property that the sum of the interior angles is 180 degrees, we can calculate the unknown angle with ease and precision.

Quiz

Tips and Tricks

1. Using the Triangle Sum Theorem

Tip: To find the measure of the third angle, subtract the sum of the known angles from 180 degrees using the Triangle Sum Theorem.

2. Using Known Angles

Tip: If one or two angles of a triangle are known, you can easily find the measure of the third angle by subtracting the sum of the known angles from 180 degrees. For example, if $∠ A = 4 0^{\circ}$ and $∠ B = 6 0^{\circ}$ , then $∠ C = 18 0^{\circ} - 4 0^{\circ} - 6 0^{\circ} = 8 0^{\circ}$ .

3. Utilizing Parallel Lines

Tip: When parallel lines intersect with a triangle, alternate interior angles are equal. This property, combined with the Triangle Sum Theorem, simplifies angle calculations.

4. Identifying Exterior Angles

Tip: When extending a side of a triangle to form an exterior angle, remember that this angle lies outside the triangle.

Real life application

Scenario: Architectural Design
Architects and designers frequently apply the Triangle Sum Theorem when creating structures with triangular elements. By understanding the theorem’s properties, they can ensure the accurate placement and alignment of triangular components in architectural designs, contributing to the stability and aesthetics of the structure.

FAQ's

What is the Triangle Sum Theorem?

The Triangle Sum Theorem states that the sum of the interior angles of a triangle is always equal to 180 degrees.

What are the properties of the Triangle Sum Theorem?

The properties of the Triangle Sum Theorem include the fact that the sum of the three interior angles of any triangle is always 180 degrees, regardless of the type of triangle (acute, obtuse, or right-angled).

How is the Triangle Sum Theorem applied in geometry?

In geometry, the Triangle Sum Theorem is utilized to calculate the measure of an unknown angle in a triangle when the measures of the other two angles are known.

What are the implications of the Triangle Sum Theorem?

The implications of the Triangle Sum Theorem extend to various geometric problems and proofs, providing a fundamental principle for understanding the relationships between the angles of a triangle.

Can the Triangle Sum Theorem be applied to any type of triangle?

Yes, the Triangle Sum Theorem is applicable to all types of triangles, including equilateral, isosceles, scalene, acute, obtuse, and right-angled triangles.

Like? Share it with your friends

Triangle Sum Theorem – Properties and Examples

Table of Contents

Introduction