Understanding the Isosceles Triangle
Table of Contents
Introduction
Isosceles Triangle
In the realm of geometry, the isosceles triangle holds a significant place due to its unique properties and applications. Let’s delve into the world of isosceles triangles and explore their definition, properties, area, and angles.
Analogy of Definition
What is an Isosceles Triangle?
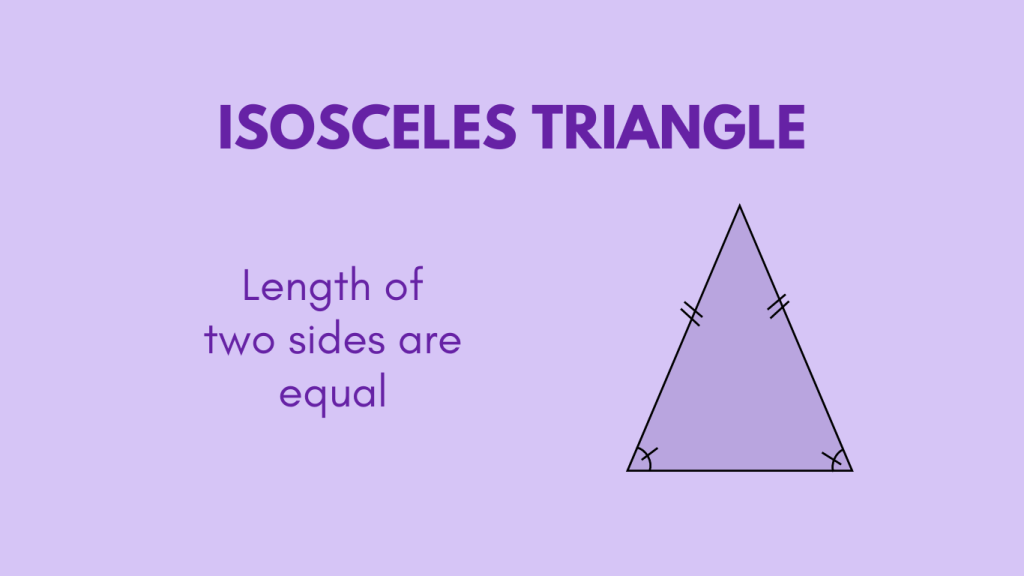
An isosceles triangle is a type of triangle that possesses two sides of equal length and two corresponding angles of equal measure. This distinctive characteristic sets it apart from other types of triangles.
Method
Properties of an Isosceles Triangle
The key properties of an isosceles triangle include having two sides of equal length, two base angles of equal measure, and a vertex angle that is different from the base angles. These properties contribute to the unique nature of the isosceles triangle.
- The vertex of an isosceles triangle is the point where the two equal sides, known as the legs, meet. It is the opposite point to the base of the triangle.
- The angles opposite the equal sides are also equal to each other.
- The perpendicular from the vertex angle to the base of an isosceles triangle bisects the base, forming two congruent segments.
- The perpendiculr from the vertex also bisects the vertex angle.
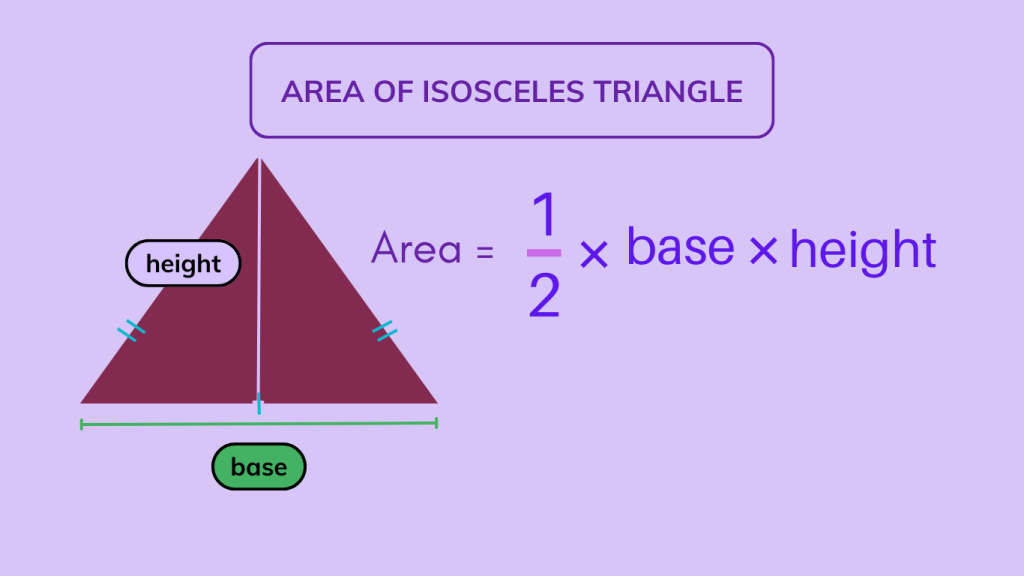
Area of Isosceles Triangle
Examples
Example 1: Calculating the Area of an Isosceles Triangle:
Summary::
This example demonstrates the method of calculating the area of an isosceles triangle by utilizing the formula: Area = (base length * height) / 2. By following the specified steps, the area of the isosceles triangle can be accurately determined, showcasing the practical application of the area formula in geometry.
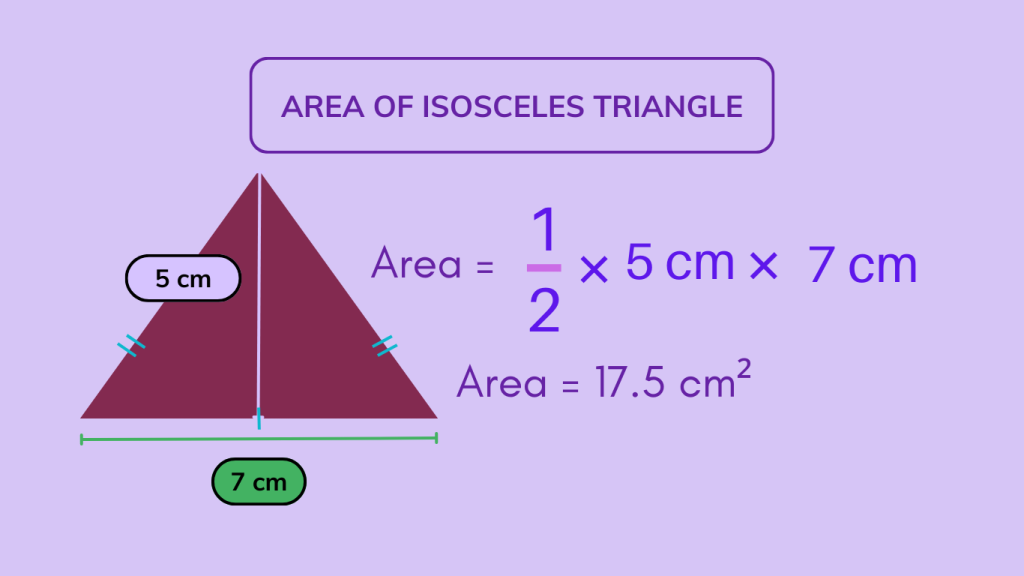
This example demonstrates the method of calculating the area of an isosceles triangle by utilizing the formula: Area = (base length * height) / 2. By following the specified steps, the area of the isosceles triangle can be accurately determined, showcasing the practical application of the area formula in geometry.
Quiz
Tips and Tricks
1. Recognize the Equal Sides
Tip: Look for triangles with two sides of equal length. If two sides match in length, it’s likely an isosceles triangle.
2. Use Base Angles
Tip: Remember that in an isosceles triangle, the angles opposite the equal sides (the base angles) are also equal. If you know one base angle, you automatically know the other.
3. Find the Vertex Angle
Tip: The angle formed by the two equal sides (the vertex angle) is larger than either of the base angles. If you’re given the vertex angle, you can find each base angle by dividing the remaining angle equally.
4. Use Symmetry
Tip: Because of its symmetry, the median from the vertex angle to the base of an isosceles triangle divides the base into two equal segments. This means if you have the length of one segment, you automatically know the length of the other.
5. Use Altitude
Tip: The altitude drawn from the vertex angle to the base of an isosceles triangle creates two right triangles. You can often use the Pythagorean theorem or trigonometric ratios to find side lengths or angle measures.
Real life application
Scenario: Architectural Design
Isosceles triangles are frequently utilized in architectural design to create symmetrical and aesthetically pleasing structures. The use of isosceles triangles in architectural elements such as gables, dormers, and arches showcases their significance in design and construction.
Scenario: Engineering and Construction
Engineers and construction professionals employ the concept of isosceles triangles in the design and construction of bridges, trusses, and support structures. The symmetrical properties of isosceles triangles contribute to the stability and strength of these structures.
Scenario: Art and Design
The concept of isosceles triangles is prevalent in art and design, where symmetrical shapes and patterns are utilized to create visually appealing compositions. From geometric art to architectural blueprints, isosceles triangles play a vital role in the creative realm.
FAQ's
An isosceles triangle is a type of triangle that has two sides of equal length and two corresponding angles of equal measure.
The properties of an isosceles triangle include having two sides of equal length, two base angles of equal measure, and a vertex angle that is different from the base angles.
The area of an isosceles triangle can be calculated using the formula: Area = (base length * height) / 2.
The angles of an isosceles triangle consist of two base angles of equal measure and a vertex angle that is different from the base angles.
The concept of an isosceles triangle finds practical applications in various real-life scenarios such as architecture, engineering, and design, where symmetrical structures and shapes are essential.
Like? Share it with your friends
Facebook
Twitter
LinkedIn