Long Multiplication – Step-by-Step Guide
Table of Contents
Introduction
Long Multiplication
Long multiplication is a fundamental arithmetic operation that involves multiplying multi-digit numbers. It is a crucial skill in mathematics and provides the foundation for more advanced mathematical concepts. In this article, we will explore the concept of long multiplication and learn how to perform it effectively.
Analogy of Definition
What is Long Multiplication?
Long multiplication is the process of multiplying numbers with multiple digits by breaking down the multiplication into smaller, simpler steps. It involves multiplying each digit of one number by each digit of the other number and then adding the results together to obtain the final product.
Method
How To Do Long Multiplication?
The process of long multiplication can be broken down into the following steps:
Step 1: Write the two numbers to be multiplied, one below the other, with the digits aligned properly.
Step 2: Starting from the rightmost digit of the bottom number, multiply it by each digit of the top number, one at a time.
Step 3: Write the results of each multiplication below the line, shifted to the left according to their position.
Step 4: Add up all the partial products to obtain the final result.
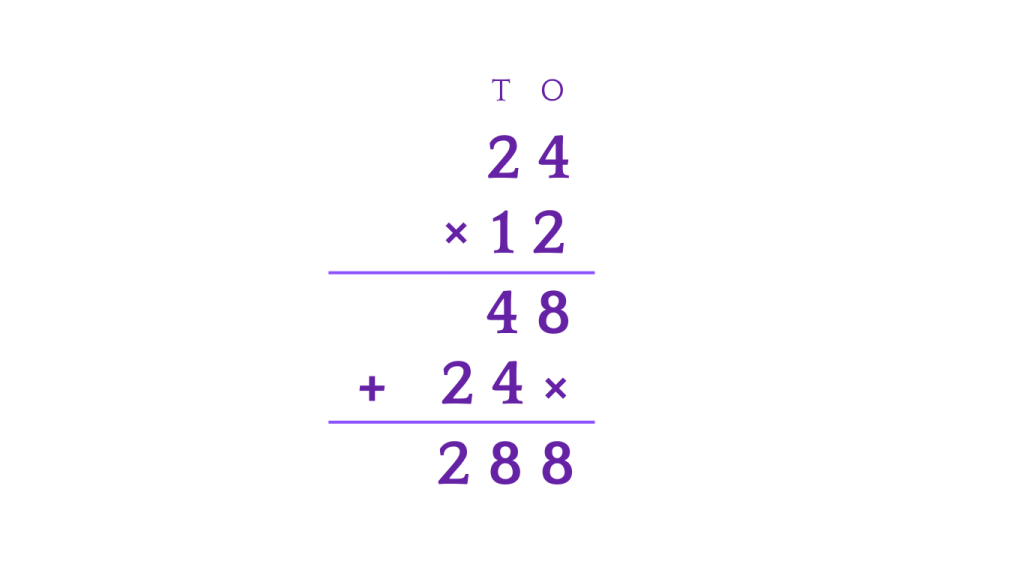
Let’s understand the concept by multiplying 24 by 12.
Step 1: We will first write 12 below 24, to begin with the multiplication .
Step 2: We will then multiply the righ-most digit of the number, meaning we will multiply both 1 and 2 by 4, which gives us 48.
Step 3: We will then move on to the second digit of the bottom number, multiplying 1 and 2 by 2 gives us 12, which will be witten below 48 but will be shifted towards left by a digit.
Step 4: We will finish up the multiplicaton by adding all the partial products, and our final answer is 488.
Examples
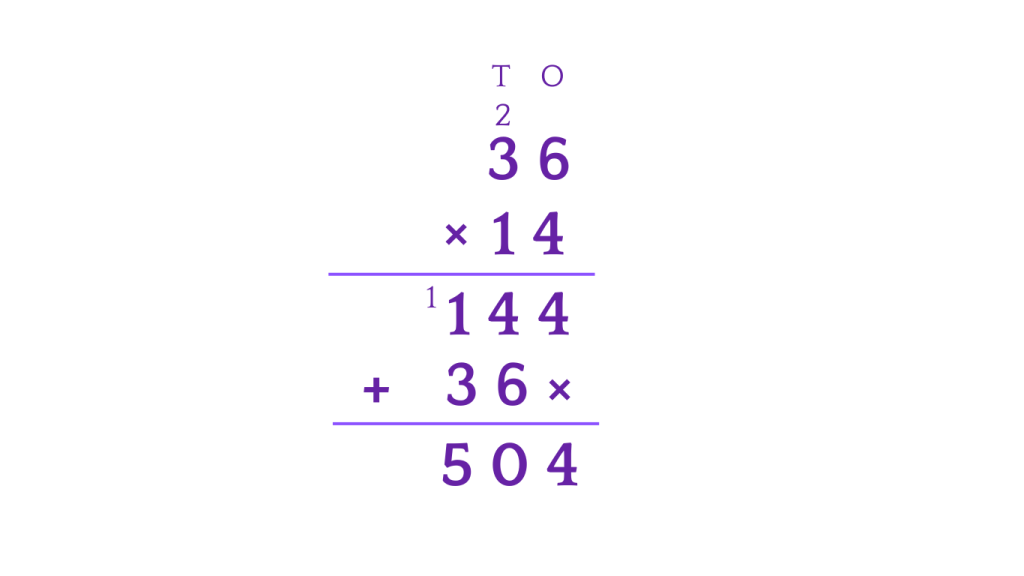
Example 1: Long Multiplication with Regrouping.
Let’s multiply 36 and 14 to see how we can do regrouping in long multiplication.
Step 1: We will first write 14 below 36, to begin with the multiplication .
Step 2: We will then multiply the righ-most digit of the number, meaning we will multiply both 1 and 4 by 6. We will put 2 in the tens column and write 4 in the product. We will then multiply 4 by 3 and add 2 to the product, which will be 14, so the product of 36 and 4 will be 144.
Step 3: We will then move on to the second digit of the bottom number, multiplying 3 and 6 by 1 gives us 36, which will be shifted towards left by a digit.
Step 4: We will finish up the multiplicaton by adding all the partial products, and our final answer is 504.
Quiz
Tips and Tricks
1. Break it Down
Tip: Break down larger numbers into smaller, more manageable parts. For example, in the multiplication of 23 and 45, you can break 23 into 20 and 3, and 45 into 40 and 5.
2. Line up Digits
Tip: When multiplying multi-digit numbers, line up the digits vertically according to place value (ones, tens, hundreds, etc.) to ensure accuracy.
3. Use Place Value
Tip: Multiply each digit in the bottom number by each digit in the top number, starting from the right and moving left. Keep track of the place value and carry over as needed.
4. Focus on One Digit at a Time
Tip: Focus on one digit at a time, starting with the rightmost digit, and work your way leftward. This helps prevent errors and keeps the process organized.
5. Use Mental Math
Tip: Break down larger calculations into smaller, more manageable steps. For example, instead of multiplying 67 by 23 in one step, you can break it down into (60 × 20) + (60 × 3) + (7 × 20) + (7 × 3).
Real life application
Story: “The Long Multiplication Adventure of Alex and Lily”
Alex and Lily, two young math enthusiasts, embarked on an exciting journey that required them to apply the concept of long multiplication to overcome various challenges.
Challenge 1: The Treasure Hunt
Alex and Lily stumbled upon a treasure map that led them to a series of cryptic clues. One of the clues required them to calculate the product of 789 and 23 using long multiplication. By applying their knowledge of long multiplication, they successfully decoded the clue and uncovered the next step in their quest.
Challenge 2: The Magical Bridge
As they ventured further, Alex and Lily encountered a magical bridge guarded by a mystical creature. The creature presented them with a mathematical puzzle that involved multiplying multi-digit numbers. With their expertise in long multiplication, Alex and Lily solved the puzzle and gained access to the other side of the bridge.
Challenge 3: The Enchanted Garden
In the final challenge, Alex and Lily found themselves in an enchanted garden filled with mysterious symbols and numerical puzzles. They utilized long multiplication to decipher the hidden messages and unlock the secrets of the garden, ultimately completing their adventure triumphantly.
FAQ's
Mastering long multiplication is essential for performing complex mathematical calculations and solving real-world problems. It lays the groundwork for understanding higher-level mathematical concepts and is a valuable skill in various academic and professional fields.
Long multiplication enables individuals to efficiently calculate the product of multi-digit numbers, which is crucial in solving a wide range of mathematical and practical problems. It provides a systematic approach to handling large numerical computations with precision and accuracy.
Yes, long multiplication has practical applications in everyday life, such as calculating measurements, determining costs, and solving logistical challenges. It is a versatile skill that can be utilized in fields such as finance, engineering, and scientific research.
The key steps to performing long multiplication accurately include aligning the digits properly, multiplying each digit of one number by each digit of the other number, and adding the partial products together to obtain the final result. Attention to detail and precision is crucial in mastering long multiplication.
Improving proficiency in long multiplication requires practice, patience, and a thorough understanding of the underlying principles. Engaging in regular exercises, seeking guidance from educators, and applying long multiplication to real-life scenarios can enhance one’s skills in this fundamental arithmetic operation.
Like? Share it with your friends
Facebook
Twitter
LinkedIn