What is Multiplication? – Definition, Symbol and Examples
Table of Contents
Introduction
Multiplication
Multiplication is a fundamental operation in mathematics that involves combining groups of numbers to find the total quantity. It is a versatile concept that is used in various mathematical and real-life scenarios. In this article, we will delve into the properties of multiplication, its application in different contexts, and the methods for performing multiplication.
Analogy of Definition
Multiplication Symbol
The multiplication symbol, represented by “×” or “*”, is a fundamental notation in mathematics, indicating the operation of multiplying two or more numbers together. Widely used and universally recognized, it provides a concise and standardized way to express multiplication operations in mathematical expressions and calculations, serving as a key tool for conveying mathematical processes across various contexts and disciplines.
Multiplication Formula
Multiplication is the process of repeated addition or combining equal groups to find the total quantity. It involves three key components: the multiplier, the multiplicand, and the product. The multiplier is the number of groups, the multiplicand is the number of items in each group, and the product is the total quantity obtained by combining the groups.
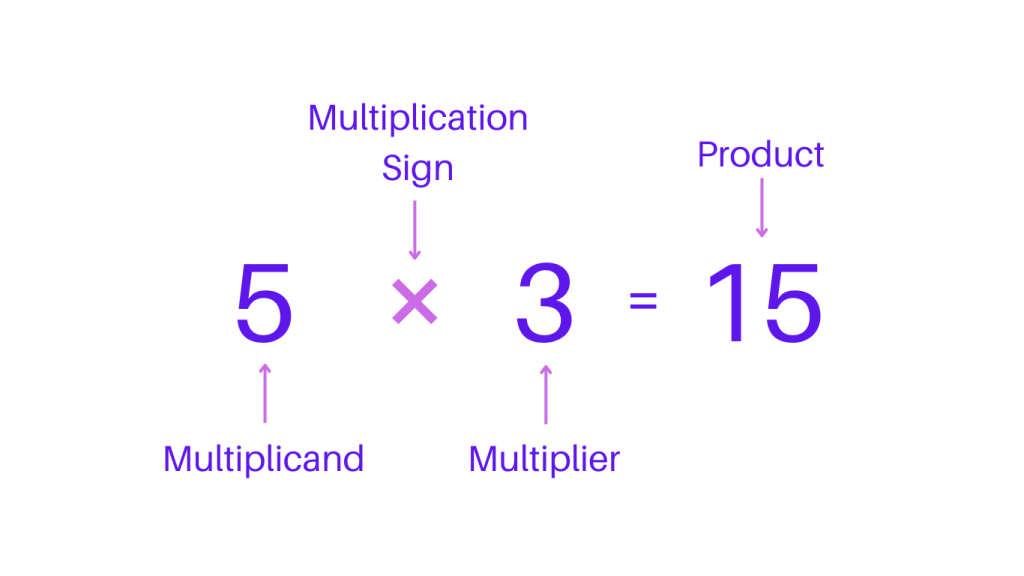
Properties of Multiplication
The properties of multiplication encompass a set of rules that define how multiplication operations behave. These properties include the commutative property, associative property, distributive property, and identity property.
Commutative Property
The commutative property of multiplication states that the order of the numbers being multiplied does not affect the result. In other words, for any two numbers a and b, the product of a and b is the same as the product of b and a.
Associative Property
The associative property of multiplication states that the grouping of the numbers being multiplied does not affect the result. In other words, for any three numbers a, b, and c, the product of (a × b) × c is the same as the product of a × (b × c).
Distributive Property
The distributive property of multiplication over addition states that multiplying a number by the sum of two other numbers is the same as multiplying the number by each of the two numbers and then adding the products together. In other words, for any three numbers a, b, and c, a × (b + c) = (a × b) + (a × c).
Method
How To Do Multiplication?
There are various methods for performing multiplication. Each method offers a unique approach to solving multiplication problems and can be applied based on the given numbers and the preferred approach. One of the primary methods involves multiplying digits individually and then adding the results, a process often referred to as multiplication without regrouping. However, when dealing with multi-digit numbers, regrouping may be necessary to ensure accuracy. Additionally, leveraging the multiplication table, a grid displaying the products of multiplying numbers from 1 to 10 (or higher), can greatly aid in memorizing multiplication facts and facilitating quicker calculations. Understanding these fundamental principles and tools lays the groundwork for mastering various methods of multiplication, ensuring efficiency and accuracy in mathematical computations.
Multiplication without Regrouping
Multiplication without regrouping is a foundational concept in arithmetic, providing a simple introduction to the process of multiplication before tackling more complex problems involving regrouping. It involves multiplying each digit of one number by each digit of the other number without carrying over any digits to the next higher place value. This basic level of multiplication is essential for building a solid understanding of the multiplication operation. Let’s illustrate this with an example:
Example: Multiply 241 by 2.
Solution:
Step 1: Start with the digit in ones place., which is 1 so 1 × 2 = 2
Step 2: We then move to multiply 2 the digit in tens place, so 4 × 2 = 8
Step 3: Now, we multiply 2 with the digit in hundreds place, so 2 × 2 = 4
Step 4: 241 × 2 = 482.

Multiplication with Regrouping
When multiplying more than two numbers with regrouping, particularly when dealing with numbers resulting in a two-digit product, we encounter the need to carry over to the next higher place value. Let’s explore this concept further using an illustrative example.
Let’s explore the process of multiplying 3826 by 7, a scenario where we need to regroup and carry over to the next higher place value:
Step 1: We start with the ones place, multiplying 7 by 6, resulting in 42 ones. This translates to 4 tens and 2 ones. We carry over the 4 tens to the tens column.
Step 2: Moving to the tens place, we multiply 7 by 2, resulting in 14 tens. Adding the carry-over of 4 from the previous step, we get 18 tens. We carry over the 1 to the hundreds column.
Step 3: Continuing to the hundreds place, we multiply 7 by 8, yielding 56 hundreds. Adding the carry-over from the previous step (1), we get 57 hundreds. We carry over the 5 to the thousands column.
Step 4: Proceeding to the thousands place, we multiply 7 by 3, resulting in 21 thousands. Adding the carry-over from the previous step (5), we get 26 thousands.
Step 5: Therefore, the product of 3826 × 7 equals 26782.
In this example, each step involves multiplying 7 by the corresponding digit of 3826 and appropriately carrying over any excess to the next higher place value. This systematic approach ensures an accurate calculation of the final product, providing a clear demonstration of multiplication with regrouping.

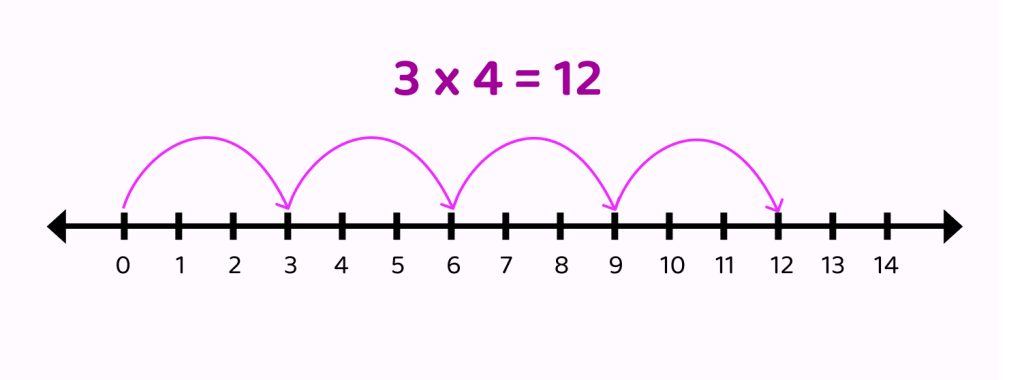
Multiplication with Number Line
Multiplying on a number line is a way to use a visual tool—a line marked with numbers—to understand multiplication better. Imagine the line starts at zero and stretches to the right. Each number on the line represents a point. To multiply a number, like 3, by another number, like 4, on the number line, we make jumps of the same size (in this case, 3) a certain number of times (in this case, 4). Each jump represents one multiplication. So, if we jump 3 units four times, as represented in the number line below, we’ll land at the point that shows the answer, which is 12. This method helps us see how multiplication works step by step.
Examples
Example 1: Multiplication without regrouping
Multiply 121 by 3

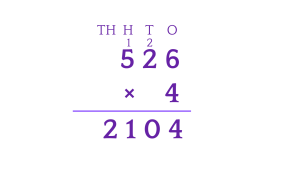
Example 2: Multiplication with regrouping
Multiply 526 by 4
Quiz
Tips and Tricks
1. Learn Multiplication Tables
Tip: Memorizing multiplication tables from 1 to 10 (or beyond) can greatly speed up mental calculations.
2. Use Commutative Property
Tip: Remember that multiplication is commutative, meaning the order of the numbers doesn’t affect the result. For example, 3 × 4 is the same as 4 × 3.
3. Break Down Larger Numbers
Tip: Break down larger numbers into smaller, more manageable factors. For example, to multiply 6 by 8, you can think of it as (3 × 2) × (4 × 2) = 24.
4. Use Doubling and Halving
Tip: Doubling and halving can simplify multiplication. For example, to multiply 7 by 8, you can double 7 to get 14 and then halve 8 to get 4, resulting in 14 × 4 = 56.
5. Use Patterns
Tip: Look for patterns in multiplication, such as multiples of 10, powers of 2, or repeated digits.
Real life application
Story: “The Multiplication Quest of Mia and Max”
Mia and Max, two adventurous siblings, embarked on a quest that required them to apply the concept of multiplication in various real-life scenarios.
Challenge 1: The Baking Adventure
Mia and Max decided to bake cookies for a charity event. They needed to calculate the total number of cookies they could make by multiplying the number of batches by the number of cookies in each batch. Using the concept of multiplication, they determined that they could bake 120 cookies in total.
Challenge 2: The Garden Project
As part of a community project, Mia and Max were tasked with planting trees in rows. They used the concept of multiplication to calculate the total number of trees needed by multiplying the number of rows by the number of trees in each row. They determined that they needed 150 trees to complete the project.
Challenge 3: The Art Class Project
In their art class, Mia and Max were assigned a project that involved arranging art supplies in boxes. They used multiplication to calculate the total number of supplies needed by multiplying the number of boxes by the number of supplies in each box. They determined that they needed 240 supplies in total.
FAQ's
Like? Share it with your friends

