Understanding Ray in Geometry
Table of Contents
Introduction
Ray
In the realm of geometry, the concept of a ray holds significant importance. Let’s delve into the definition and properties of a ray in geometry to gain a comprehensive understanding of its role in mathematical and real-world contexts.
Analogy of Definition
What is a Ray?
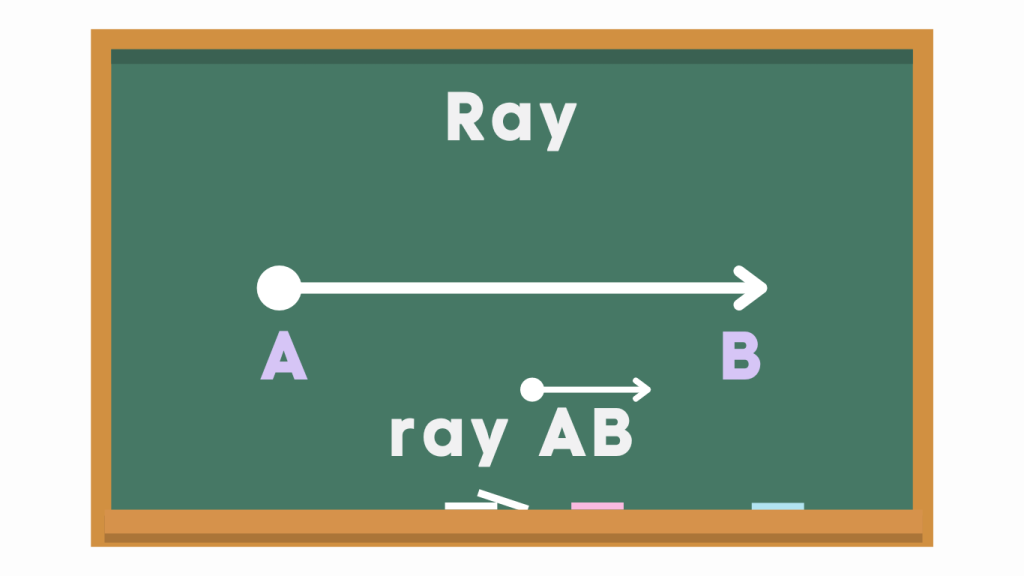
A ray is a part of a line that has one endpoint and extends infinitely in one direction. It stretches out infinitely in front of you, but it doesn’t have an end. Rays are used in geometry to talk about directions, positions and forms angles.
Naming a Ray
Naming a ray is pretty straightforward. You just need to use two points: one to show where the ray starts and one to show the direction it goes.
For example, let’s say you have a ray starting at point A and going through point B. To name this ray, you would call it “ray AB.”
Remember, it’s important to mention the starting point first, followed by the point in the direction the ray goes. This helps us understand where the ray begins and where it’s headed.
Method
Properties of a Ray
1. Starting Point: A ray has a starting point where it originates. This point is where the ray begins its journey.
2. Direction: A ray extends infinitely in one direction from its starting point. It doesn’t have an endpoint in that direction.
3. No Endpoint in One Direction: A ray has no endpoint in the direction it extends. It continues indefinitely in that direction.
4. Endpoint: A ray has an endpoint in the opposite direction from its starting point. This endpoint marks the end of the ray in that direction.
5. One-Dimensional: Rays are one-dimensional geometric objects, meaning they have only length and no width or thickness.
6. Representation: A ray can be represented by drawing an arrow starting from its starting point and extending infinitely in one direction.
Examples
Example 1: Ray AB
Definition: Ray AB starts at point A and extends infinitely in the direction of point B.
Example 2: Ray CD
Definition: Ray CD begins at point C and extends infinitely in the direction of point D.
Example 3: Ray EF
Definition: Ray EF originates at point E and extends infinitely in the direction of point F.
Summary:
These examples illustrate the concept of a ray in geometry, showcasing how a ray starts at a specific endpoint and extends infinitely in a particular direction. Understanding the properties and applications of rays is essential in various mathematical and real-world scenarios.
These examples illustrate the concept of a ray in geometry, showcasing how a ray starts at a specific endpoint and extends infinitely in a particular direction. Understanding the properties and applications of rays is essential in various mathematical and real-world scenarios.
Quiz
Tips and Tricks
1. Naming a Ray
Tip: When naming a ray, always use the endpoint first, followed by any other point on the ray, with an arrow symbol indicating the direction of the ray.
2. Bisecting a Ray
Tip: To bisect a ray, draw a perpendicular line from the endpoint to the ray, dividing it into two equal parts.
3. Identifying Rays in Nature
Tip: Look for real-life examples of rays in nature, such as sun rays, laser beams, and the path of light from a flashlight.
Real life application
Scenario: Solar Energy Collection
Solar panels utilize the concept of rays to collect and convert sunlight into energy. The panels are strategically positioned to capture the maximum amount of sunlight, harnessing the power of rays for sustainable energy production.
Scenario: Architectural Design
Architects and designers use the principles of rays in geometry to create innovative building designs that optimize natural light and airflow, enhancing the overall functionality and aesthetics of the structure.
FAQ's
A ray in geometry is a part of a line that has one endpoint and extends infinitely in one direction. It is represented by a single lowercase letter with a symbol over it to indicate the direction of the ray.
The properties of a ray in geometry include having one endpoint, extending infinitely in one direction, and being named using the endpoint and any other point on the ray.
A ray has one endpoint and extends infinitely in one direction, while a line segment has two endpoints and a finite length.
Yes, a ray can be bisected by drawing a perpendicular line from the endpoint to the ray, dividing it into two equal parts.
Real-life examples of rays in geometry include sun rays, laser beams, and the path of light from a flashlight.
Like? Share it with your friends
Facebook
Twitter
LinkedIn