Simplifying Fractions – Methods with Examples
Table of Contents
Introduction
Simplifying Fractions
Fraction is a part of a whole. In other words, fractions make a whole. It has two main parts, numerator, and denominator, wihch represents the whole. Whether dealing with any operations related to fraction, the ability to simplify fractions is a fundamental concept that every student should master. Let’s explore the art of simplifying fractions and understand its significance in mathematical operations.
Analogy of Definition
The Concept of Simplifying Fractions
Simplifying a fraction involves reducing it to its simplest form by dividing both the numerator and the denominator by their Highest Common Factor. The goal is to express the fraction in its lowest terms, where the numerator and denominator have no common factors other than 1. We need to simplify while multiplying fractions as well as while adding and subtracting them.
Method
Techniques for Simplifying Fractions
There are various methods for simplifying fractions. One common method is to find the Highest Common Factor (HCF) of the numerator and denominator and then divide both by the HCF to simplify the fraction. Another approach involves using prime factorization to simplify the fraction to its lowest terms.
Using HCF Method for Simplifying Fractions
Simplifying the Fraction 12/18
Step 1: Find the Highest Common Factor (HCF) of 12 and 18
The factors of 12 are 1, 2, 3, 4, 6, and 12
The factors of 18 are 1, 2, 3, 6, 9, and 18
The HCF of 12 and 18 is 6
Step 2: Divide both the numerator and denominator by the HCF
12 ÷ 6 = 2
18 ÷ 6 = 3
So, the simplified form of 12/18 is 2/3.
Using Prime Factorization to Simplify Fractions
Simplifying the Fraction 12/18
Step 1: Find the prime factorization of 12 and 18
The prime factors of 12 are 2 × 2 × 3
The prime factors of 18 are 2 × 3 × 3
Step 2: Identify the common prime factors and cancel them out. In this case , the common factors are 2 and 3.
Step 3: After cancelling out the common factors, we multiply the remaining numbers in the numerator and denominator.
Hence, the smplified form of 12/18 is 2/3.
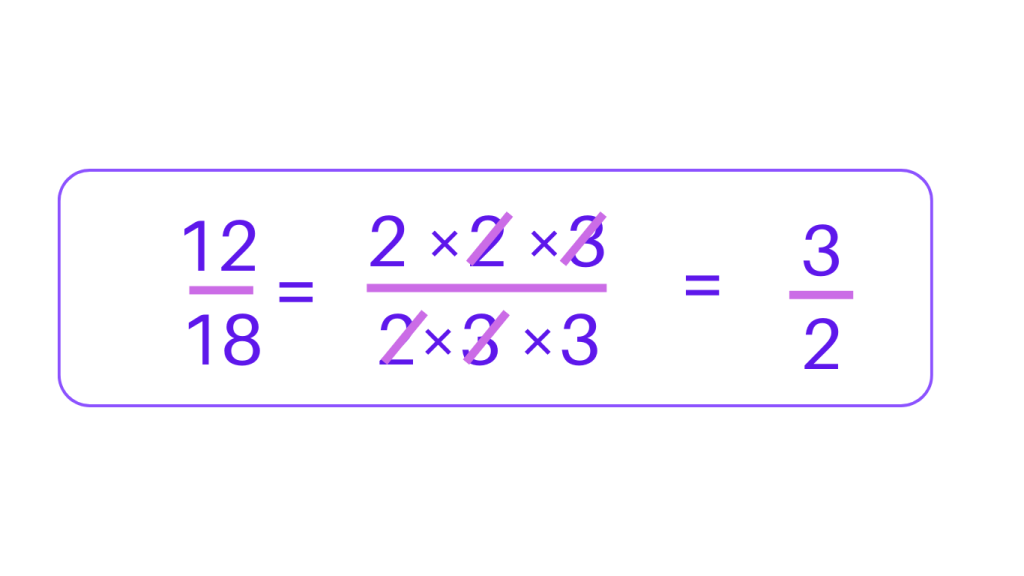
Do you want to learn more about fractions? Do visit our site ChimpVine for more.
Examples
Example: Simplify the fraction 15/25
Step 1: Find the Highest Common Factor (HCF) of 15 and 25.
The factors of 15 are 1, 3, 5, and 15.
The factors of 25 are 1, 5, and 25.
The HCF of 15 and 25 is 5.
Step 2: Divide both the numerator and denominator by the HCF
15 ÷ 5 = 3
25 ÷5 = 5
So, the simplified fraction is 3/5
Quiz
Tips and Tricks
1. Simplifying Proper Fractions
Tip: To simplify a proper fraction, find the Highest Common Factor (HCF) of the numerator and denominator, and then divide both by the HCF to express the fraction in its lowest terms.
2. Simplifying Improper Fractions
Tip: When simplifying an improper fraction, follow the same process of finding the HCF and dividing both the numerator and denominator by the HCF to reduce the fraction to its simplest form
3. Simplifying Mixed Fractions
Tip: To simplify a mixed fraction, convert it to an improper fraction, find the HCF of the numerator and denominator, and then divide both by the HCF to express the fraction in its lowest terms.
Real life application
Story: “The Fraction Simplification Challenge”
Emma and Noah, two adventurous students, encountered real-life scenarios where the ability to simplify fractions proved to be invaluable in solving practical problems.
Challenge 1: Baking a Cake
Emma and Noah decided to bake a cake and found a recipe that required 3/4 cup of flour. However, they only had 6/8 cup of flour available. By simplifying the fraction 6/8 to its simplest form, which is 3/4, they were able to use the exact amount of flour needed for the recipe.
Challenge 2: Sharing Pizza Slices
During a pizza party, Emma and Noah wanted to share 10/12 of a pizza equally among their friends. By simplifying the fraction 10/12 to 5/6, they were able to divide the pizza into equal portions without any leftovers.
Challenge 3: Measuring Ingredients
In a science experiment, Emma and Noah needed 15/20 of a liter of a liquid solution. By simplifying the fraction 15/20 to 3/4, they accurately measured the required amount of the solution for their experiment.
FAQ's
Simplifying fractions is important because it helps in expressing fractions in their lowest terms, making calculations and comparisons easier. It also allows for a clearer understanding of the relationship between different fractions.
Proper fractions have a smaller numerator than the denominator, improper fractions have a larger numerator than the denominator, and mixed fractions consist of a whole number and a proper fraction.
Yes, all fractions can be simplified to their lowest terms by finding the Highest Common Factor (HCF) of the numerator and denominator and then dividing both by the HCF.
Simplifying fractions is essential in real-life situations such as cooking, baking, measurements, and sharing quantities among a group. It ensures accurate and precise calculations in various everyday scenarios.
To simplify a mixed fraction, convert it to an improper fraction, find the Highest Common Factor (HCF) of the numerator and denominator, and then divide both by the HCF to express the fraction in its lowest terms.
By mastering the art of simplifying fractions, students can enhance their problem-solving skills and apply this fundamental concept to various mathematical and real-life scenarios.
Like? Share it with your friends
Facebook
Twitter
LinkedIn