Understanding Adjacent Angles

Introduction

Adjacent Angles

In the realm of geometry, the concept of adjacent angles plays a crucial role in understanding the relationships between angles and their properties. Let’s delve into the world of adjacent angles and explore their significance in geometric calculations and problem-solving.

Analogy of Definition

What are Adjacent Angles?

Adjacent angles refer to two angles that share a common vertex and a common side but do not overlap. In simpler terms, they are angles that are side by side and do not intersect. In the following figure, we can see that ∠DAC and ∠ DAB are adjacent, as they share a same vertex, A, and same side AD.

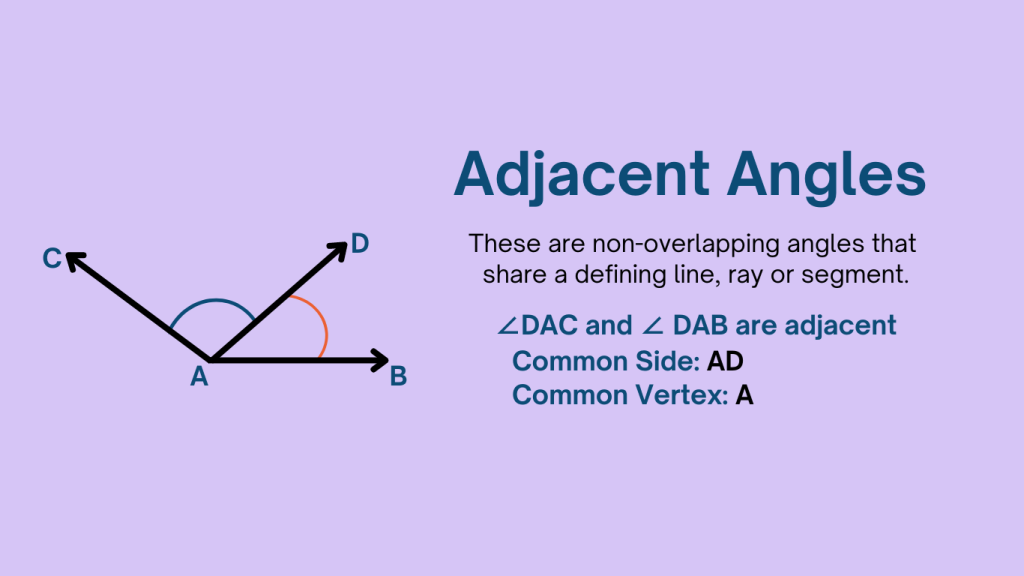
Method

Properties of Adjacent Angles

Adjacent angles have a few key properties that help in understanding their relationships in geometry:

Common Vertex and Side: Adjacent angles share a common vertex and a common side, which means they sit next to each other on the same plane.
No Overlap: Despite sharing a side, adjacent angles do not overlap. Their interiors do not intersect.
Linear Pair: When adjacent angles form a straight line, they are called a linear pair. The sum of the angles in a linear pair is always 180°, making them supplementary.

These properties are essential in identifying and working with adjacent angles in various geometric problems.

Identifying Adjacent Angles

Common Vertex: Adjacent angles always share the same vertex, which is the point where the two angles meet. This is the first clue that two angles might be adjacent.

Common Side: In addition to sharing a vertex, adjacent angles also share one side or ray. This common side lies between the two angles, forming a boundary for both.
For example, if two angles are formed by three rays coming from a single point (vertex), and two of these rays form a boundary between the angles, those angles are adjacent.

Examples

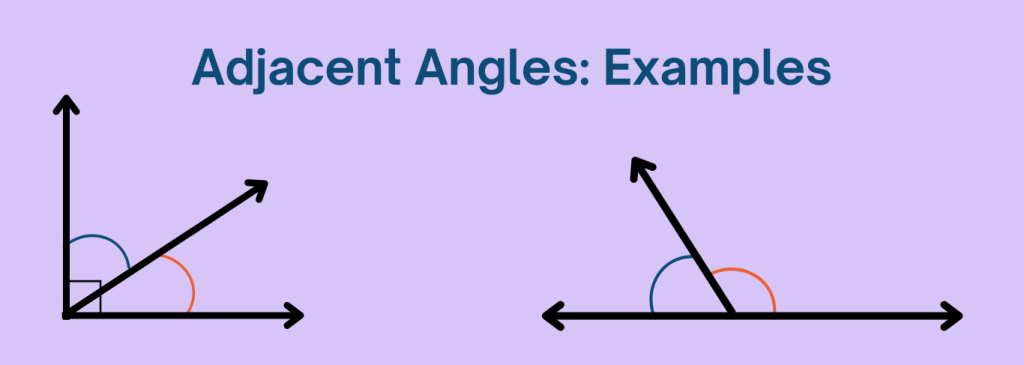
Quiz

Tips and Tricks

1. Identifying Adjacent Angles

Tip: To identify adjacent angles, look for angles that share a common vertex and a common side without overlapping.

2. Calculating the Sum of Adjacent Angles

Tip: When adjacent angles form a linear pair (meaning they are on the same line), their sum is always 180°, making them supplementary. But in other cases, such as when adjacent angles are part of a polygon or other figures, their sum can be less than or more than 180°.

3. Real-Life Applications of Adjacent Angles

Tip: Adjacent angles are used in architectural designs to ensure proper alignment and symmetry.The angles are adjacent and contribute to the aesthetic appeal of the structure.

Real life application

Real-Life Applications of Adjacent Angles:

Scenario: Architectural Design
Architects utilize the concept of adjacent angles in designing building facades, ensuring that the angles formed by intersecting lines are visually appealing and structurally sound.

Scenario: Engineering Drawings
Engineers use adjacent angles to create precise and accurate drawings for construction projects, ensuring that the angles formed by structural elements are properly aligned and interconnected.

Scenario: Navigation and Orientation
In navigation, adjacent angles are used to determine the direction and orientation of objects and landmarks, aiding in accurate positioning and mapping of geographical locations.